Câu 26. Cho hai đường tròn (C):(x-2)^ 2 +(y-2)^ 2 =9;(C' ):x^ 2 +y^ 2 +4x-8y+11=0 ,biết (C) và (C') đối xứng nhau qua đường thẳng (a) .Phương trình của (a) là : A. 2x + 2y - 4 = 0 B.2x-y+3=0 . C. x + y - 4 = 0 . D. 2x + 2y = 0 .

Những câu hỏi liên quan
câu 1.cho đường tròn (c) : \(x^2+y^2+4x+4y-17=0\). viết phương trình tiếp tuyến của (C) biết tiếp tuyến tạo với Õ một góc \(60^0\)
câu 2. cho hai đường trong (c1)\(x^2+y^2-2x-2y=0\), (c2) \(x^2+y^2-4x-6y-3=0\) viết phương trình tiếp tuyến chung của 2 đường tròn
1.
Tạo với Ox là tạo với tia Ox hay trục hoành nhỉ? 2 cái này khác nhau đấy. Tạo với tia Ox thì chỉ có 1 góc 60 độ theo chiều dương, tạo với trục hoành thì có 2 góc 60 và 120 đều thỏa mãn. Coi như tạo tia Ox đi
Đường tròn tâm \(I\left(-2;-2\right)\) bán kính \(R=5\)
\(tan60^0=\sqrt{3}\Rightarrow\) tiếp tuyến có hệ số góc bằng \(\sqrt{3}\Rightarrow\) pt có dạng:
\(y=\sqrt{3}x+b\Leftrightarrow\sqrt{3}x-y+b=0\)
\(d\left(I;d\right)=R\Leftrightarrow\dfrac{\left|-2\sqrt{3}+2+b\right|}{\sqrt{3+1}}=5\)
\(\Leftrightarrow\left|b+2-2\sqrt{3}\right|=10\Rightarrow\left[{}\begin{matrix}b=8+2\sqrt{3}\\b=-12+2\sqrt{3}\end{matrix}\right.\)
Có 2 tiếp tuyến: \(\left[{}\begin{matrix}\sqrt{3}x-y+8+2\sqrt{3}=0\\\sqrt{3}x-y-12+2\sqrt{3}=0\end{matrix}\right.\)
Đúng 1
Bình luận (1)
2.
(C1) có tâm \(I\left(1;1\right)\) bán kính \(R_1=\sqrt{2}\)
(C2) có tâm \(J\left(2;3\right)\) bán kính \(R_2=4\)
Gọi tiếp tuyến chung d có pt: \(ax+by+c=0\)
\(\left\{{}\begin{matrix}d\left(I;d\right)=R_1\\d\left(J;d\right)=R_2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{\left|a+b+c\right|}{\sqrt{a^2+b^2}}=\sqrt{2}\\\dfrac{\left|2a+3b+c\right|}{\sqrt{a^2+b^2}}=4\end{matrix}\right.\)
\(\Rightarrow2\sqrt{2}\left|a+b+c\right|=\left|2a+3b+c\right|\)
? Đề nghiêm túc đấy chứ? Cho kiểu này thì sấp mặt, tối thiểu pt (C1) cũng có dạng \(x^2+y^2-2x-2y+1=0\) để học sinh còn thở chứ.
Đúng 0
Bình luận (2)
Ủa, nhìn lại thì bài 2 người ta cho đề kiểu hack não.
\(\overrightarrow{IJ}=\left(1;2\right)\Rightarrow IJ=\sqrt{5}< R_2-R_1=4-\sqrt{2}\)
Do đó \(\left(C_2\right)\) chứa \(\left(C_1\right)\) nên ko tồn tại tiếp tuyến chung của 2 đường tròn
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
26 tháng 9 lúc 14:31 Cho hai đường thẳng (d): y (m − 2)x + 1& (d ) : y m^2x − 2x + m. 1) Tìm m biết (D) // (D’). 2) Với m tìm được ở câu 2 hãy a) Vẽ đồ thị (D); b) Tính góc tạo bởi đường thẳng (D) và trục Ox; c) Tính chu vi và diện tích tam giác được tạo bởi đường thẳng (D), Ox, Oy; d) Tính khoảng cách từ gốc tọa độ O đến đường thẳng (D). 4) chứng minh rằng đường thẳng (D) luôn đi qua một điểm cố định khi m thay đổi
Đọc tiếp
26 tháng 9 lúc 14:31
Cho hai đường thẳng (d): y = (m − 2)x + 1& (d' ) : y = m^2x − 2x + m.
1) Tìm m biết (D) // (D’).
2) Với m tìm được ở câu 2 hãy
a) Vẽ đồ thị (D);
b) Tính góc tạo bởi đường thẳng (D) và trục Ox;
c) Tính chu vi và diện tích tam giác được tạo bởi đường thẳng (D), Ox, Oy;
d) Tính khoảng cách từ gốc tọa độ O đến đường thẳng (D).
4) chứng minh rằng đường thẳng (D) luôn đi qua một điểm cố định khi m thay đổi
1: (D): \(y=\left(m-2\right)x+1\)
(D'): \(y=m^2x-2x+m=x\left(m^2-2\right)+m\)
Để (D)//(D') thì \(\left\{{}\begin{matrix}m^2-2=m-2\\m< >1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m^2-m=0\\m< >1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\left(m-1\right)=0\\m< >1\end{matrix}\right.\Leftrightarrow m=0\)
2:
a: Khi m=0 thì (D): \(y=\left(0-2\right)x+1=-2x+1\)
(D'): \(y=x\left(0^2-2\right)+0=-2x\)
b: Gọi \(\alpha\) là góc tạo bởi (D) với trục Ox
(D): y=-2x+1
=>a=-2
\(tan\alpha=a=-2\)
=>\(\alpha\simeq116^034'\)
c: (D): y=-2x+1; (D'): y=-2x
Gọi A,B lần lượt là giao điểm của (D) với trục Ox và Oy
Ox\(\perp\)Oy nên OA\(\perp\)OB
Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\-2x+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\-2x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0,5\\y=0\end{matrix}\right.\)
Vậy: A(0,5;0)
\(OA=\sqrt{\left(0,5-0\right)^2+\left(0-0\right)^2}=0,5\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=-2x+1=-2\cdot0+1=1\end{matrix}\right.\)
vậy:B(0;1)
\(OB=\sqrt{\left(0-0\right)^2+\left(1-0\right)^2}=1\)
ΔOAB vuông tại O
=>\(OA^2+OB^2=AB^2\)
=>\(AB^2=1^2+0,5^2=1,25\)
=>\(AB=\sqrt{1,25}=\dfrac{\sqrt{5}}{2}\)
Chu vi tam giác OAB là: \(C_{OAB}=OA+OB+AB=1,5+\dfrac{\sqrt{5}}{2}=\dfrac{3+\sqrt{5}}{2}\)
Diện tích tam giác OAB là:
\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot1\cdot0,5=0,25\)
d: (D): y=-2x+1
=>2x+y-1=0
Khoảng cách từ O đến (D) là:
\(d\left(O;\left(D\right)\right)=\dfrac{\left|0\cdot2+0\cdot1-1\right|}{\sqrt{2^2+1^2}}=\dfrac{1}{\sqrt{5}}\)
4: (D): y=(m-2)x+1
=mx-2x+1
Tọa độ điểm cố định mà (D) luôn đi qua là:
\(\left\{{}\begin{matrix}x=0\\y=-2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-2\cdot0+1=1\end{matrix}\right.\)
Đúng 2
Bình luận (0)
cho đường tròn (c) pt: \(\left(x+1\right)^2+y^2=9.\) viết PT đường thẳng đi qua A(2;3) cắt đường tròn (c) tại 2 điểm M,N so cho MN=6
Đường tròn (C) tâm \(I\left(-1;0\right)\) bán kính \(R=3\)
\(MN=6=2R\Rightarrow MN\) là đường kính
\(\Rightarrow\) Đường thẳng d đi qua tâm I của đường tròn
\(\Rightarrow\) Đường thẳng d là đường thẳng IA
\(\overrightarrow{IA}=\left(3;3\right)=3\left(1;1\right)\Rightarrow\) đường thẳng d nhận (1;-1) là 1 vtpt
Phương trình d:
\(1\left(x-2\right)-1\left(y-3\right)=0\Leftrightarrow x-y+1=0\)
Đúng 1
Bình luận (0)
cho đường tròn (c) (x-4)^2+(y-1)^2=9 và delta x-y+5=0. Tìm tọa độ M thuộc delta sao cho từ M kẻ được 2 tiếp tuyến đến đường tròn mà 2 tiếp tuyến đó vuông góc nhau
Gọi \(M=\left(m;m+5\right)\left(m\in\right)R\) là điểm cần tìm.
\(\Rightarrow IM=\sqrt{2m^2+32}\)
Ta có: \(cos\left(AM;IM\right)=cos45^o\)
\(\Leftrightarrow\dfrac{R}{IM}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\dfrac{3}{\sqrt{2m^2+32}}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\) vô nghiệm
Vậy không tồn tại điểm M thỏa mãn yêu cầu bài toán.
Đúng 1
Bình luận (0)
cho đường tròn (C) : x^2+y^2-2x=9 và điểm A( 0;1). tìm tọa độ 2 điểm B,C thuộc đường tròn sao cho tam giác ABC vuông cân tại A
Đường tròn (C) tâm \(I\left(1;0\right)\) bán kính \(R=\sqrt{10}\)
Do tam giác ABC vuông cân tại A \(\Rightarrow AB=AC\)
Lại có \(IB=IC=R\)
\(\Rightarrow AI\) là trung trực BC \(\Rightarrow AI\) đồng thời là phân giác \(\widehat{BAC}\)
\(\Rightarrow\widehat{IAB}=45^0\)
\(\overrightarrow{AI}=\left(1;-1\right)\), do B thuộc đường tròn, gọi tọa độ B có dạng: \(B\left(x;y\right)\) với \(x^2+y^2-2x-9=0\)
\(\Rightarrow\overrightarrow{AB}=\left(x;y-1\right)\)
\(cos\widehat{IAB}=\dfrac{\sqrt{2}}{2}=\dfrac{\left|1.x-1\left(y-1\right)\right|}{\sqrt{2}.\sqrt{x^2+\left(y-1\right)^2}}\)
\(\Rightarrow\sqrt{x^2+y^2-2y+1}=\left|x-y+1\right|\)
\(\Rightarrow x^2+y^2-2y+1=x^2+y^2+1-2xy+2x-2y\)
\(\Rightarrow x-xy=0\Rightarrow x\left(1-y\right)=0\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y^2=9\Rightarrow y=\pm3\\y=1\Rightarrow x^2-2x-8=0\Rightarrow x=\left\{4;-2\right\}\end{matrix}\right.\)
Vậy tọa đô các điểm B;C tương ứng là: \(\left[{}\begin{matrix}\left(0;3\right);\left(-2;1\right)\\\left(0;-3\right);\left(4;1\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
trong số cá đường tròn sau, đường tròn nào tiếp xúc với trục Ox?
A. \(x^2+y^2-2x+10y=0\)
B. \(x^2+y^2-10y+1=0\)
C. \(x^2+y^2-5=0\)
D. \(x^2+y^2+6x+5y+9=0\)
C. \(x^2+y^2-5=0\)
Do đường tròn tiếp xúc với trục Ox nên R = d(I,Ox) = |yI|.
Phương trình trục Ox là y = 0
Đáp án D đúng vì: Tâm I(−3;\(\dfrac{-5}{2}\)) và bán kính R=\(\dfrac{5}{2}\). Ta có
d(I, Ox) = |yI| = R.
Đúng 1
Bình luận (0)
Câu 1: Cho đường tròn (C) (x - 1)2 + (y - 2)2 = 29 và điểm M(6;2). Đường thẳng (d) đi qua M và cắt đường tròn tại A,B sao cho AB = 4
Câu 2: Mặt phẳng Oxy cho đường thẳng d: x + y + 2 = 0, thực hiện liên tiếp phép Q(o;-90o) và phép đối xứng qua trục △ : x + 2 = 0 biến đường thẳng d thành d'. Đường thẳng d' có phương trình là?
1.
Vãi, tui làm một lúc rồi mới biết đề bài không có yêu cầu.
Đúng 0
Bình luận (0)
Cho đường tròn (C): (x - 1
)
2
+ (y + 3
)
2
10 và đường thẳng Δ: x + y + 1 0, biết đường tròn (C) cắt Δ tại hai điểm phân biệt A và B. Độ dài đoạn thẳng AB bằng: A.
19
2
B.
38
C.
19
2
D.
38
2
Đọc tiếp
Cho đường tròn (C): (x - 1 ) 2 + (y + 3 ) 2 = 10 và đường thẳng Δ: x + y + 1 = 0, biết đường tròn (C) cắt Δ tại hai điểm phân biệt A và B. Độ dài đoạn thẳng AB bằng:
A. 19 2
B. 38
C. 19 2
D. 38 2
Chọn B.
Vì đường tròn (C) cắt Δ tại hai điểm phân biệt A và B nên tọa độ điểm A và B là nghiệm của hệ phương trình:
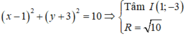
Gọi H là trung điểm của AB suy ra IH ⊥ AB ⇒ IH ⊥ Δ.
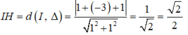
Xét tam giác AIH vuông tại H ta có:
A H 2 + I H 2 = A I 2 ⇒ A H 2 = A I 2 - I H 2
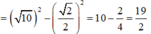
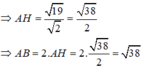
Đúng 1
Bình luận (0)
Cho đường tròn ( C )÷(x-3)^2+ ( y+ 6 )^2= 36. Tìm ảnh của ( C ) qua phép vị tự tâm 0(0;0 ) , tỉ số 4 - tỉ số k = 1/3 A (x+9)^2 + (y-18)^2=4 B (x-1)^2+(y+2)^2=4 C (x+1)^2+(y-2)^2=36 D (x+9)^2+(y-18)^2=36


















