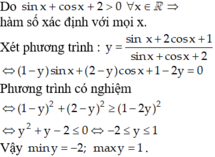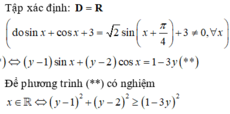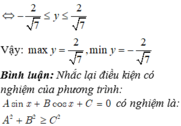tìm GTNN và GTLN của hàm số y=3-2cosx+3cos2x
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6

Những câu hỏi liên quan
Tìm GTLN và GTNN của hàm số
y
sin
x
+
2
cos
x
+
1
sin
x
+
cos
x
+
3
(*)
Đọc tiếp
Tìm GTLN và GTNN của hàm số y = sin x + 2 cos x + 1 sin x + cos x + 3 (*)
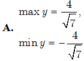
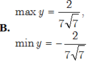


Tìm GTLN và GTNN của hàm số sau:
y
sin
x
+
2
cos
x
+
1
sin
x
+
cos
x
+...
Đọc tiếp
Tìm GTLN và GTNN của hàm số sau: y = sin x + 2 cos x + 1 sin x + cos x + 2
A. min y = 0, max y = 1
B. min y= -2, max y= 1
C. min y =-1, max y= 1
D. Tất cả sai
Tìm GTLN và GTNN của hàm số : 1. y = sinx + 2cosx +1 / 2sinx + cosx + 3
2.y= 2sin^2sinx - 3 sinx cosx + cos^2 x
Giải phương trình : 1. 2sin^2 * 2x + sin7x -1 = sinx
2.cos 4x + 12 sin^2 x -1 = 0
Tìm GTLN và GTNN của hàm số y = 3 + sin2x
21.
a) `2sin(x-30^@)-1=0`
`<=>sin(x-30^@)=1/2`
`<=> sin(x-30^@)=sin30^@`
`<=>[(x-30^@=30^@+k360^@),(x-30^@=180^@-30^@+k360^@):}`
`<=> [(x=60^@+k360^@),(x=180^@+k360^@):}`
b) `5sin^2x+3cosx+3=0`
`<=>5(1-cos^2x)+3cosx+3=0`
`<=>-5cos^2x+3cosx+8=0`
`<=>(cosx+1)(cosx=8/5)=0`
`<=>[(cosx=-1),(cosx=8/5\ (VN)):}`
`<=>x=180^@+k360^@`
22.
`-1<=sin2x<=1`
`<=>2<=3+sin2x<=4`
`=> y_(min)=2 ; y_(max)=4`
Đúng 1
Bình luận (0)
xét tính chẵn lẻ của hàm số sau :
\(y=\frac{3tan^3x-5sinx}{2+cosx}\)
\(y=\frac{sinx}{x^4-3x^2+2}\)
Tìm GTLN GTNN của hàm số sau
y= sinx + cosx
\(y=\sqrt{2cosx+3}-4\)
\(y=sin^4x+cos^4x\)
Xét tính chẵn lẻ:
a) TXĐ: D = R \ {π/2 + kπ| k nguyên}
Với mọi x thuộc D ta có (-x) thuộc D và
\(f\left(-x\right)=\frac{3\tan^3\left(-x\right)-5\sin\left(-x\right)}{2+\cos\left(-x\right)}=-\frac{3\tan^3x-5\sin x}{2+\cos x}=-f\left(x\right)\)
Vậy hàm đã cho là hàm lẻ
b) TXĐ: D = R \ \(\left\{\pm\sqrt{2};\pm1\right\}\)
Với mọi x thuộc D ta có (-x) thuộc D và
\(f\left(-x\right)=\frac{\sin\left(-x\right)}{\left(-x\right)^4-3\left(-x\right)^2+2}=-\frac{\sin x}{x^4-3x^2+2}=-f\left(x\right)\)
Vậy hàm đã cho là hàm lẻ
Đúng 0
Bình luận (0)
Tìm GTLN, GTNN:
TXĐ: D = R
a) Ta có (\(\left(\sin x+\cos x\right)^2=1+\sin2x\)
Với mọi x thuộc D ta có\(-1\le\sin2x\le1\Leftrightarrow0\le1+\sin2x\le2\Leftrightarrow0\le\left(\sin x+\cos x\right)^2\le2\)
\(\Leftrightarrow0\le\left|\sin x+\cos x\right|\le\sqrt{2}\Leftrightarrow-\sqrt{2}\le\sin x+\cos x\le\sqrt{2}\)
Vậy \(Min_{f\left(x\right)}=-\sqrt{2}\) khi \(\sin2x=-1\Leftrightarrow2x=-\frac{\pi}{2}+k2\pi\Leftrightarrow x=-\frac{\pi}{4}+k\pi\)
\(Max_{f\left(x\right)}=\sqrt{2}\) khi\(\sin2x=1\Leftrightarrow x=\frac{\pi}{4}+k\pi\)
b) Với mọi x thuộc D ta có:
\(-1\le\cos x\le1\Leftrightarrow-2\le2\cos x\le2\Leftrightarrow1\le2\cos x+3\le5\)
\(\Leftrightarrow1\le\sqrt{2\cos x+3}\le\sqrt{5}\Leftrightarrow5\le\sqrt{2\cos x+3}+4\le\sqrt{5}+4\)
Vậy\(Min_{f\left(x\right)}=5\) khi \(\cos x=-1\Leftrightarrow x=\pi+k2\pi\)
\(Max_{f\left(x\right)}=\sqrt{5}+4\) khi \(\cos x=1\Leftrightarrow x=k2\pi\)
c) \(y=\sin^4x+\cos^4x=\left(\sin^2x+\cos^2x\right)^2-2\sin^2x\cos^2x\)\(=1-\frac{1}{2}\left(2\sin x\cos x\right)^2=1-\frac{1}{2}\sin^22x\)
Với mọi x thuộc D ta có: \(0\le\sin^22x\le1\Leftrightarrow-\frac{1}{2}\le-\frac{1}{2}\sin^22x\le0\Leftrightarrow\frac{1}{2}\le1-\frac{1}{2}\sin^22x\le1\)
Đến đây bạn tự xét dấu '=' xảy ra khi nào nha :p
Đúng 0
Bình luận (0)
1. Tìm tham số m để phương trình 3cos2x-7=2m có nghiệm?
2. Trên đoạn \([0;2\pi]\) , phương trình \(2cos^2x-\sqrt{3}cosx=0\)có bao nhiêu nghiệm?
3. Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số \(y=\sqrt{2cosx-3m+14}\) xác định với mọi x thuộc R?
Help me!!!
1.
\(3cos2x-7=2m\)
\(\Leftrightarrow cos2x=\dfrac{2m-7}{3}\)
Phương trình đã cho có nghiệm khi:
\(-1\le\dfrac{2m-7}{3}\le1\)
\(\Leftrightarrow2\le m\le5\)
Đúng 1
Bình luận (0)
2.
\(2cos^2x-\sqrt{3}cosx=0\)
\(\Leftrightarrow cosx\left(2cosx-\sqrt{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\pm\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\) Có 4 nghiệm \(\dfrac{\pi}{2};\dfrac{3\pi}{2};\dfrac{\pi}{6};\dfrac{11\pi}{6}\) thuộc đoạn \(\left[0;2\pi\right]\)
Đúng 1
Bình luận (0)
Tìm GTLN M và GTNN m của hàm số \(y=\sqrt{6-2x}+\sqrt{3+2x}\)
\(y\le\sqrt{2\left(6-2x+3+2x\right)}=3\sqrt{2}\)
\(y_{max}=3\sqrt{2}\) khi \(x=\dfrac{3}{4}\)
\(y\ge\sqrt{6-2x+3+2x}=3\)
\(y_{min}=3\) khi \(\left[{}\begin{matrix}x=3\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm GTLN và GTNN của hàm số
y
sin
x
+
2
cos
x
+
1
sin
x
+
cos
x
+
3
(*) A.
m
a
x
y
4...
Đọc tiếp
Tìm GTLN và GTNN của hàm số y = sin x + 2 cos x + 1 sin x + cos x + 3 (*)
A. m a x y = 4 7 , m i n y = - 4 7
B. m a x y = 2 7 7 , m i n y = - 2 7 7
C. m a x y = 7 2 , m i n y = - 2 7
D. m a x y = 2 7 7 , m i n y = - 2 7 7
Tìm GTLN và GTNN của hàm số y = √3cosx - sinx
\(y=\sqrt{3}cosx-sinx=2\left(\dfrac{\sqrt{3}}{2}cosx-\dfrac{1}{2}sinx\right)=2cos\left(x+\dfrac{\pi}{6}\right)\)
Vì \(cos\left(x+\dfrac{\pi}{6}\right)\in\left[-1;1\right]\Rightarrow y=\sqrt{3}cosx-sinx\in\left[-2;2\right]\)
\(\Rightarrow y_{min}=-2\Leftrightarrow cos\left(x+\dfrac{\pi}{6}\right)=-1\Leftrightarrow x+\dfrac{\pi}{6}=\pi+k2\pi\Leftrightarrow x=\dfrac{5\pi}{6}+k2\pi\)
\(y_{max}=2\Leftrightarrow cos\left(x+\dfrac{\pi}{6}\right)=1\Leftrightarrow x+\dfrac{\pi}{6}=k2\pi\Leftrightarrow x=-\dfrac{\pi}{6}+k2\pi\)
Đúng 0
Bình luận (0)
Tìm GTLN và GTNN của hàm số: y = |sinx + cos2x|
Đặt \(sinx=t\left(t\in\left[-1;1\right]\right)\)
\(y=\left|sinx+cos2x\right|=\left|2sin^2x-sinx-1\right|\)
\(\Leftrightarrow y=\left|f\left(t\right)\right|=\left|2t^2-t-1\right|\)
\(f\left(-1\right)=2\Rightarrow y=2\)
\(f\left(1\right)=0\Rightarrow y=0\)
\(f\left(\dfrac{1}{4}\right)=-\dfrac{9}{8}\Rightarrow y=\dfrac{9}{8}\)
\(\Rightarrow y_{min}=0;y_{max}=2\)
Đúng 0
Bình luận (0)