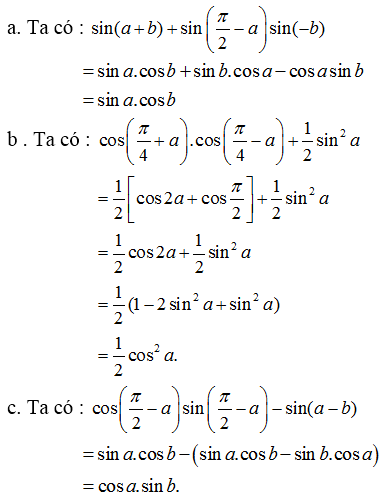rút gọn : sin(a-pi/4)cos(pi/3-a)-cos(pi/4-a)sin(pi/3-a)

Những câu hỏi liên quan
rút gọn : sin(pi/4-a)+cos(pi/4-a)/sin(pi/4-a)-cos(pi/4-a)
1. Cho 2cosleft(alpha+betaright)cosalphacosleft(pi+betaright)Tính Adfrac{1}{2sin^2alpha+3cos^2alpha}+dfrac{1}{2sin^2beta+3cos^2beta}2. Rút gọn: a) A4cosdfrac{2x}{3}cosdfrac{pi+2x}{3}cosdfrac{pi-2x}{3}b) Bdfrac{sinleft(a-bright).sinleft(a+bright)}{cos^2a.sin^2b}-tan^2a.cot^2b3. Chứng minh rằng: Nếu 2tan atanleft(a+bright) thì:a) sin bsin a.cosleft(a+bright)b) 3sin bsinleft(2a+bright)
Đọc tiếp
1. Cho \(2\cos\left(\alpha+\beta\right)=\cos\alpha\cos\left(\pi+\beta\right)\)
Tính \(A=\dfrac{1}{2\sin^2\alpha+3\cos^2\alpha}+\dfrac{1}{2\sin^2\beta+3\cos^2\beta}\)
2. Rút gọn: a) \(A=4\cos\dfrac{2x}{3}\cos\dfrac{\pi+2x}{3}\cos\dfrac{\pi-2x}{3}\)
b) \(B=\dfrac{\sin\left(a-b\right).\sin\left(a+b\right)}{\cos^2a.\sin^2b}-\tan^2a.\cot^2b\)
3. Chứng minh rằng: Nếu \(2\tan a=\tan\left(a+b\right)\) thì:
a) \(\sin b=\sin a.\cos\left(a+b\right)\)
b) \(3\sin b=\sin\left(2a+b\right)\)
1.
\(2cos\left(a+b\right)=cosa.cos\left(\pi+b\right)\)
\(\Leftrightarrow2cosa.cosb-2sina.sinb=-cosa.cosb\)
\(\Leftrightarrow2sina.sinb=3cosa.cosb\Rightarrow4sin^2a.sin^2b=9cos^2a.cos^2b\)
\(\Rightarrow4\left(1-cos^2a\right)\left(1-cos^2b\right)=9cos^2a.cos^2b\)
\(\Leftrightarrow4-4\left(cos^2a+cos^2b\right)=5cos^2a.cos^2b\)
\(A=\dfrac{1}{cos^2a+2\left(sin^2a+cos^2a\right)}+\dfrac{1}{cos^2b+2\left(sin^2b+cos^2b\right)}\)
\(=\dfrac{1}{2+cos^2a}+\dfrac{1}{2+cos^2b}=\dfrac{4+cos^2a+cos^2b}{4+2\left(cos^2a+cos^2b\right)+cos^2a.cos^2b}\)
\(=\dfrac{4+cos^2a+cos^2b}{4+2\left(cos^2a+cos^2b\right)+\dfrac{4}{5}-\dfrac{4}{5}\left(cos^2a+cos^2b\right)}=\dfrac{4+cos^2a+cos^2b}{\dfrac{24}{5}+\dfrac{6}{5}\left(cos^2a+cos^2b\right)}=\dfrac{5}{6}\)
Đúng 1
Bình luận (0)
2.
\(A=2cos\dfrac{2x}{3}\left(cos\dfrac{2\pi}{3}+cos\dfrac{4x}{3}\right)=2cos\dfrac{2x}{3}\left(cos\dfrac{4x}{3}-\dfrac{1}{2}\right)\)
\(=2cos\dfrac{2x}{3}.cos\dfrac{4x}{3}-cos\dfrac{2x}{3}\)
\(=cos3x+cos\dfrac{2x}{3}-cos\dfrac{2x}{3}\)
\(=cos3x\)
\(B=\dfrac{cos2b-cos2a}{cos^2a.sin^2b}-tan^2a.cot^2b=\dfrac{1-2sin^2b-\left(1-2sin^2a\right)}{cos^2a.sin^2b}-tan^2a.cot^2b\)
\(=\dfrac{2sin^2a-2sin^2b}{cos^2a.sin^2b}-tan^2a.cot^2b=2tan^2a\left(1+cot^2b\right)-2\left(1+tan^2a\right)-tan^2a.cot^2b\)
\(=2tan^2a+2tan^2a.cot^2b-2-2tan^2a-tan^2a.cot^2b\)
\(=tan^2a.cot^2b-2\)
Đúng 3
Bình luận (0)
3.
\(\dfrac{2sina}{cosa}=\dfrac{sin\left(a+b\right)}{cos\left(a+b\right)}\Leftrightarrow2sina.cos\left(a+b\right)=cosa.sin\left(a+b\right)\)
\(\Leftrightarrow sina.cos\left(a+b\right)=sin\left(a+b\right).cosa-cos\left(a+b\right)sina\)
\(\Leftrightarrow sina.cos\left(a+b\right)=sin\left(a+b-a\right)\)
\(\Leftrightarrow sina.cos\left(a+b\right)=sinb\)
b.
\(\dfrac{2sina}{cosa}=\dfrac{sin\left(a+b\right)}{cos\left(a+b\right)}\Leftrightarrow2sina.cos\left(a+b\right)=cosa.sin\left(a+b\right)\)
\(\Leftrightarrow sin\left(2a+b\right)+sin\left(-b\right)=\dfrac{1}{2}sin\left(2a+b\right)+\dfrac{1}{2}sinb\)
\(\Leftrightarrow\dfrac{1}{2}sin\left(2a+b\right)=\dfrac{3}{2}sinb\)
\(\Leftrightarrow sin\left(2a+b\right)=3sinb\)
Đúng 1
Bình luận (0)
tính
a)A= \(sin^2\frac{\pi}{3}+sin^2\frac{\pi}{9}+sin^2\frac{7\pi}{18}+sin^2\frac{\pi}{6}\)
b) B= \(sin^2\frac{\pi}{6}+sin^2\frac{\pi}{3}+sin^2\frac{\pi}{4}+sin^2\frac{9\pi}{4}+tan\frac{\pi}{6}.cot\frac{\pi}{6}\)
c) C= \(cos^215+cos^225+cos^235+cos^245+cos^2105+cos^2115+cos^2125\)
rút gọn biểu thức:
A= cosa.sin( b-c )+ cosb. sin(c-a) + cosc.sin( a-b)
B= \(sin^2x+cos\left(\frac{\pi}{3}-x\right).cos\left(\frac{\pi}{3}+x\right)\)
C=\(sin^2x+sin^2\left(\frac{2\pi}{3}+x\right)+sin^2\left(\frac{2\pi}{3}-x\right)\)
D=\(sin^2\left(\frac{\pi}{4}+x\right)-sin^2x-2sinx.sin\frac{\pi}{4}.cos\left(\frac{\pi}{4}+x\right)\)
\(A=cosa\left(sinb.cosc-cosb.sinc\right)+cosb\left(sinc.cosa-cosc.sina\right)+cosc\left(sinacosb-cosasinb\right)\)
\(A=cosasinbcosc-cosacosbsinc+cosacosbsinc-sinacosbcosc+sinacosbcosc-cosasinbcosc\)
\(A=0\)
\(B=sin^2x+\frac{1}{2}\left(cos\frac{2\pi}{3}+cos2x\right)\)
\(B=\frac{1}{2}-\frac{1}{2}cos2x-\frac{1}{4}+\frac{1}{2}cos2x\)
\(B=\frac{1}{4}\)
\(C=\frac{1}{2}-\frac{1}{2}cos2x+\frac{1}{2}-\frac{1}{2}cos\left(\frac{4\pi}{3}+2x\right)+\frac{1}{2}-\frac{1}{2}cos\left(\frac{4\pi}{3}-2x\right)\)
\(C=\frac{3}{2}-\frac{1}{2}cos2x-\frac{1}{2}\left(cos\left(\frac{4\pi}{3}+2x\right)+cos\left(\frac{4\pi}{3}-2x\right)\right)\)
\(C=\frac{3}{2}-\frac{1}{2}cos2x-cos\frac{4\pi}{3}.cos2x\)
\(C=\frac{3}{2}-\frac{1}{2}cos2x+\frac{1}{2}cos2x\)
\(C=\frac{3}{2}\)
\(D=\frac{1}{2}\left[\sqrt{2}sin\left(\frac{\pi}{4}+x\right)\right]^2-sin^2x-sinx.\sqrt{2}cos\left(\frac{\pi}{4}+x\right)\)
\(D=\frac{1}{2}\left(sinx+cosx\right)^2-sin^2x-sinx\left(sinx-cosx\right)\)
\(D=\frac{1}{2}\left(1+2sinx.cosx\right)-sin^2x-sin^2x+sinx.cosx\)
\(D=\frac{1}{2}+sinxcosx+sinxcosx=\frac{1}{2}+sin2x\)
Đúng 0
Bình luận (0)
Góc độ cao của thang dựa vào tường là 60º và chân thang cách tường 4,6 m. Chiều dài của thang là
Đúng 0
Bình luận (0)
Rút gọn các biểu thức :
a) \(\sin\left(a+b\right)+\sin\left(\dfrac{\pi}{2}-a\right)\sin\left(-b\right)\)
b) \(\cos\left(\dfrac{\pi}{4}+a\right)\cos\left(\dfrac{\pi}{4}-a\right)+\dfrac{1}{2}\sin^2a\)
c) \(\cos\left(\dfrac{\pi}{2}-a\right)\sin\left(\dfrac{\pi}{2}-b\right)-\sin\left(a-b\right)\)
rút gọn biểu thức:
E=cos(\(\dfrac{3\pi}{3}-\alpha\))-sin(\(\dfrac{3\pi}{2}-\alpha\))+sin(\(\alpha+4\pi\))
Đúng 0
Bình luận (0)
A=cos(a-pi/3)-sin(a-pi/6), rút gọn A s ạ
A=cosa.cos\(\frac{\pi}{3}\)+sina.sin\(\frac{\pi}{3}\)-sina.cos\(\frac{\pi}{6}\)+cosa.sin\(\frac{\pi}{6}\)
A=\(\frac{1}{2}\)cosa+\(\frac{\sqrt{3}}{2}\)sina-\(\frac{\sqrt{3}}{2}\)sina+\(\frac{1}{2}\)cosa
A= cosa
Đúng 0
Bình luận (0)
Rút gọn biểu thức :
A = sin(a - \(\frac{\pi}{4}\))cos(\(\frac{\pi}{3}\) - a) - cos(\(\frac{\pi}{4}\) - a)sin(\(\frac{\pi}{3}\) - a)
\(A=sin\left(a-\frac{\pi}{4}-\frac{\pi}{3}+a\right)=sin\left(2a-\frac{7\pi}{12}\right)\)
Đúng 0
Bình luận (0)
Tính \(\sin 2a,\cos 2a,\tan 2a,\;\)biết:
a) \(\sin a = \frac{1}{3}\) và \(\frac{\pi }{2} < a < \pi \);
b) \(\sin a + \cos a = \frac{1}{2}\) và \(\frac{\pi }{2} < a < \frac{{3\pi }}{4}\).
a) Vì \(\frac{\pi }{2} < a < \pi \) nên \(\cos a < 0\)
Ta có: \({\sin ^2}a + {\cos ^2}a = 1\)
\(\Leftrightarrow \frac{1}{9} + {\cos ^2}a = 1\)
\(\Leftrightarrow {\cos ^2}a = 1 - \frac{1}{9}= \frac{8}{9}\)
\(\Leftrightarrow \cos a =\pm\sqrt { \frac{8}{9}} = \pm \frac{{2\sqrt 2 }}{3}\)
Vì \(\cos a < 0\) nên \(cos a =-\frac{{2\sqrt 2 }}{3}\)
Suy ra \(\tan a = \frac{{\sin a}}{{\cos a}} = \frac{{\frac{1}{3}}}{{ - \frac{{2\sqrt 2 }}{3}}} = - \frac{{\sqrt 2 }}{4}\)
Ta có: \(\sin 2a = 2\sin a\cos a = 2.\frac{1}{3}.\left( { - \frac{{2\sqrt 2 }}{3}} \right) = - \frac{{4\sqrt 2 }}{9}\)
\(\cos 2a = 1 - 2{\sin ^2}a = 1 - \frac{2}{9} = \frac{7}{9}\)
\(\tan 2a = \frac{{2\tan a}}{{1 - {{\tan }^2}a}} = \frac{{2.\left( { - \frac{{\sqrt 2 }}{4}} \right)}}{{1 - {{\left( { - \frac{{\sqrt 2 }}{4}} \right)}^2}}} = - \frac{{4\sqrt 2 }}{7}\)
b) Vì \(\frac{\pi }{2} < a < \frac{{3\pi }}{4}\) nên \(\sin a > 0,\cos a < 0\)
\({\left( {\sin a + \cos a} \right)^2} = {\sin ^2}a + {\cos ^2}a + 2\sin a\cos a = 1 + 2\sin a\cos a = \frac{1}{4}\)
Suy ra \(\sin 2a = 2\sin a\cos a = \frac{1}{4} - 1 = - \frac{3}{4}\)
Ta có: \({\sin ^2}a + {\cos ^2}a = 1\;\)
\( \Leftrightarrow \left( {\frac{1}{2} - {\cos }a} \right)^2 + {\cos ^2}a - 1 = 0\)
\( \Leftrightarrow \frac{1}{4} - \cos a + {\cos ^2}a + {\cos ^2}a - 1 = 0\)
\( \Leftrightarrow 2{\cos ^2}a - \cos a - \frac{3}{4} = 0\)
\( \Rightarrow \cos a = \frac{{1 - \sqrt 7 }}{4}\) (Vì \(\cos a < 0)\)
\(\cos 2a = 2{\cos ^2}a - 1 = 2.{\left( {\frac{{1 - \sqrt 7 }}{4}} \right)^2} - 1 = - \frac{{\sqrt 7 }}{4}\)
\(\tan 2a = \frac{{\sin 2a}}{{\cos 2a}} = \frac{{ - \frac{3}{4}}}{{ - \frac{{\sqrt 7 }}{4}}} = \frac{{3\sqrt 7 }}{7}\)
Đúng 0
Bình luận (0)
rút gọn hệ thức : a) P = cos(\(\frac{\pi}{2}\) + x) + cos(2\(\pi\) - x) + cos(3\(\pi\) + x) ; b) Q = 2sin(\(\frac{\pi}{2}\) + x) + sin(4\(\pi\) - x) + sin(\(\frac{3\pi}{2}\) + x) + cos(\(\frac{\pi}{2}\) + x)
a) P = cos(\(\frac{\Pi}{2}\) + x) + cos(2π - x) + cos(3π + x) = -sinx + cosx - cosx = -sinx
Đúng 0
Bình luận (0)