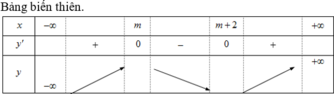
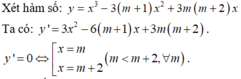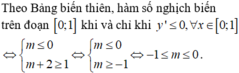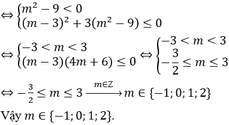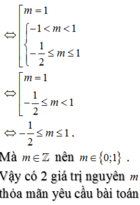Tìm m để y= x3 - (3m+1)x2 +x - 3 nghịch biến trên (1,3)

Những câu hỏi liên quan
Biết rằng S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số y
x
3
- 3(m-1)
x
2
+ 3m(m+2)x nghịch biến trên đoạn [0;1]. Tính tổng các phần tử của S? A. S 0. B. S 1. C. S -2. D. S -1.
Đọc tiếp
Biết rằng S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số y = x 3 - 3(m-1) x 2 + 3m(m+2)x nghịch biến trên đoạn [0;1]. Tính tổng các phần tử của S?
A. S = 0.
B. S = 1.
C. S = -2.
D. S = -1.
Với tất cả các giá trị thực nào của tham số m thì hàm số
y
x
3
-
3
(
m
+
1
)
x
2
+
3
m
(
m
+
2...
Đọc tiếp
Với tất cả các giá trị thực nào của tham số m thì hàm số y = x 3 - 3 ( m + 1 ) x 2 + 3 m ( m + 2 ) x nghịch biến trên đoạn [0;1]?
A. - 1 ≤ m ≤ 0
B. - 1 < m < 0
C. m ≥ - 1
D. m ≤ 0
Tìm tất cả các giá trị của m để hàm số
y
(
m
-
2
)
x
3
+
(
m
-
2
)
x
2
-
x
+
1
nghịch biến trên R. A.
-
1
m
≤
2
B.
m
≤
-...
Đọc tiếp
Tìm tất cả các giá trị của m để hàm số y = ( m - 2 ) x 3 + ( m - 2 ) x 2 - x + 1 nghịch biến trên R.
A. - 1 < m ≤ 2
B. m ≤ - 1 m ≥ 2
C. - 1 ≤ m ≤ 2
D. - 1 ≤ m < 2
Đáp án D
Với y = ( m - 2 ) x 3 + ( m - 2 ) x 2 - x + 1 ta có y ' = 3 ( m - 2 ) x 2 + 2 ( m - 2 ) x - 1
Hàm số đã cho nghịch biến trên R
⇔ m - 2 < 0 ∆ ' ≤ 0 ⇔ m < 2 m 2 - m - 2 ≤ 0 ⇔ m < 2 - 1 ≤ m ≤ 2 ⇔ 1 ≤ m ≤ 2
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị tham số m để hàm số
y
1
3
(
m
-
1
)
x
3
-
(
m
-
1
)
x
2
-
x
+
1
nghịch biến trên
ℝ
A.
m
≥
1
m
≤...
Đọc tiếp
Tìm tất cả các giá trị tham số m để hàm số y = 1 3 ( m - 1 ) x 3 - ( m - 1 ) x 2 - x + 1 nghịch biến trên ℝ
A. m ≥ 1 m ≤ 0
B. 0 ≤ m ≤ 1
C. m ≥ 1 m ≤ - 3
D. - 3 ≤ m ≤ 1
Đáp án là B.
Ta có y ' ( x ) = ( m - 1 ) x 2 - 2 ( m - 1 ) x - 1
TH1. m - 1 = 0 ⇔ m = 1 .Khi đó
y , = - 1 < 0 , ∀ x ∈ ℝ .Nên hàm só luôn nghịch biếến trên ℝ .
TH2. m - 1 ≢ 0 ⇔ m ≢ 1 .Hàm số luôn nghịch biến trên ℝ khi
y , ≤ 0 , ∀ x ∈ ℝ ⇔ ( m - 1 ) x 2 - 2 ( m - 1 ) x - 1 ≤ 0 , ∀ x ∈ ℝ ⇔ m - 1 < 0 ∆ ' ≤ 0 ⇔ m < 1 m ( m - 1 ) ≤ 0 ⇔ 0 ≤ m ≤ 1 . Kết hợp ta được 0 ≤ m < 1 .
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để hàm số
y
(
m
2
-
9
)
x
3
+
(
m
-
3
)
x
2
-
x
+
1
nghịch biến trên R A. 6 B. 4 C. 3 D. 5
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = ( m 2 - 9 ) x 3 + ( m - 3 ) x 2 - x + 1 nghịch biến trên R
A. 6
B. 4
C. 3
D. 5
a/ cho hàm số: y=(-3m - 2)x2. Tìm m để hàm số nghịch biến khi x < 0
b/ cho hàm số: y=(m2 - 2m + 3)x2. Xác định tính biến thiên của hàm số
c/ cho hàm số: y=(2m + 3)x2. Tìm m để hàm số đồng biến khi x>0
a.
Hàm số nghịch biến khi \(x< 0\Rightarrow-3m-2>0\Rightarrow m< -\dfrac{2}{3}\)
b.
Do \(a=m^2-2m+3=\left(m-1\right)^2+2>0;\forall m\)
\(\Rightarrow\) Hàm đồng biến khi \(x>0\) và nghịch biến khi \(x< 0\)
c.
Hàm đồng biến khi \(x>0\Rightarrow2m+3>0\)
\(\Rightarrow m>-\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
Có bao nhiêu giá trị nguyên m để hàm số y = ( m 2 - 1 ) x 3 + ( m - 1 ) x 2 - x + 4 nghịch biến trên R
A. 1
B. 2
C. 0
D. 3
Tìm tất cả các giá trị của tham số m để hàm số y
(
m
-
1
)
x
3
+
(
m
-
1
)
x
2
-
(
2
m
+
1
)
+
5
nghịch biến trên tập xác định. A.
-
5
4
≤
m
≤
1
B....
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số y = ( m - 1 ) x 3 + ( m - 1 ) x 2 - ( 2 m + 1 ) + 5 nghịch biến trên tập xác định.
A. - 5 4 ≤ m ≤ 1
B. - 2 7 ≤ m < 1
C. - 7 2 ≤ m < 1
D. - 2 7 ≤ m ≤ 1
Chọn D.
Tập xác định: D = ℝ
Ta có ![]()
Xét m = 1, ta có y' = -3 < 0 ∀ x ∈ ℝ nên nghịch biến trên tập xác định.
Xét m ≠ 1 Để hàm số trên nghịch biến trên tập xác định khi và chỉ khi
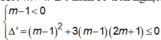
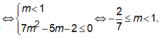
Vậy với - 2 7 ≤ m ≤ 1 thì hàm số y = ( m - 1 ) x 3 + ( m - 1 ) x 2 - ( 2 m + 1 ) + 5 nghịch biến trên tập xác định.
Đúng 0
Bình luận (0)
tìm các giá trị thực của m để y=x^3−3(m+1)x^2+3m(m+2)x−3(m+1) nghich biến trên [0;1]
tìm tất cả m để y=x^4−2m.x^2−2 đồng biến (0;+∞) trên và nghịch biến trên (−∞;0)