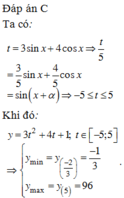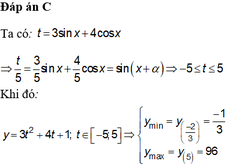Giải phương trình sau giúp mình: 3sinx+4cosx=5+(4tanx-3)^2

Những câu hỏi liên quan
Giải phương trình: 3sinx - 4cosx = 1
3sinx – 4cosx = 1 ⇔ 3/5sinx - 4/5cosx = 1/5.
⇔ sin(x – α) = 1/5 (với cosα = 3/5 , sinα = 4/5)
Đúng 0
Bình luận (0)
Giải các pt lượng giác sau:
a, 4cosx - 3sinx = √5.sin2x + √10
b, 4cosx - 3sinx = √5.sin2x
c, 4cosx - 3sinx = -5
Mn giúp mình vs ạ :3
Giải phương trình:
a,\(1+2Sinx=2Cosx\)
b,\(4Cosx-3Sinx=3\)
c,\(3Cos3x+4Sin3x=5\)
a,Pt \(\Leftrightarrow cosx-sinx=\dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{2\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+arc.cos\left(\dfrac{1}{2\sqrt{2}}\right)+k2\pi\\x=-\dfrac{\pi}{4}-arc.cos\left(\dfrac{1}{2\sqrt{2}}\right)+k2\pi\end{matrix}\right.\) ,\(k\in Z\)
b) Pt \(\Leftrightarrow\dfrac{4}{5}cosx-\dfrac{3}{5}sinx=\dfrac{3}{5}\)
Đặt \(cosa=\dfrac{4}{5}\Rightarrow sina=\dfrac{3}{5}\)
Pttt:\(cosx.cosa-sina.sinx=\dfrac{3}{5}\)
\(\Leftrightarrow cos\left(x+a\right)=\dfrac{3}{5}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-a+arc.cos\left(\dfrac{3}{5}\right)+2k\pi\\x=-a-arc.cos\left(\dfrac{3}{5}\right)+2k\pi\end{matrix}\right.\)(\(k\in Z\))
Vậy...
c) Pt\(\Leftrightarrow\dfrac{3}{5}cos3x+\dfrac{4}{5}.sin3x=1\)
Đặt \(cosa=\dfrac{3}{5}\Rightarrow sina=\dfrac{4}{5}\)
Pttt:\(cos3x.cosa+sin3a.sina=1\)
\(\Leftrightarrow cos\left(3x-a\right)=1\)
\(\Leftrightarrow x=\dfrac{a}{3}+\dfrac{k2\pi}{3}\)(\(k\in Z\))
Vậy...
Đúng 1
Bình luận (2)
1)\(1+2sinx=2cosx\)
\(\Leftrightarrow cosx-sinx=\dfrac{1}{2}\)
\(\Leftrightarrow\left(cosx-sinx\right)^2=\dfrac{1}{4}\)
\(\Leftrightarrow cosx^2+sinx^2-2cosxsinx=\dfrac{1}{4}\)
\(\Leftrightarrow1-2cosxsinx=\dfrac{1}{4}\)
\(\Leftrightarrow2cosxsinx=\dfrac{3}{4}\)
\(\Leftrightarrow sin2x=\dfrac{3}{4}\)
\(\Rightarrow\left\{{}\begin{matrix}x=arcsin\dfrac{3}{8}+k\pi\\x=\pi-arcsin\dfrac{3}{8}+k\pi\end{matrix}\right.\) \(\left(K\in Z\right)\)
b) \(4cosx-3sinx=3\)
\(\Leftrightarrow\dfrac{4}{5}cosx-\dfrac{3}{5}sinx=\dfrac{3}{5}\)
Đặt \(cosa=\dfrac{3}{5},sina=\dfrac{4}{5}\)
Khi đó:
\(sinacosx-cosasinx=\dfrac{3}{5}\)
\(\Leftrightarrow sin\left(a-x\right)=\dfrac{3}{5}\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-x=arcsin\dfrac{3}{5}+k2\pi\\a-x=\pi-arcsin\dfrac{3}{5}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=a-arcsin\dfrac{3}{5}+k2\pi\\x=a-\pi-arcsin\dfrac{3}{5}+k2\pi\end{matrix}\right.\) \(\left(k\in Z\right)\)
3)\(3cos3x+4sin3x=5\)
\(\Leftrightarrow\dfrac{3}{5}cos3x+\dfrac{4}{5}sin3x=1\)
Đặt \(sina=\dfrac{3}{5},cosa=\dfrac{4}{5}\)
khi đó: \(sinacos3x+cosasin3x=1\)
\(\Leftrightarrow sin\left(a+3x\right)=\dfrac{\pi}{2}\)
\(\Leftrightarrow3x=\dfrac{\pi}{2}-a+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}-\dfrac{1}{3}a+k\dfrac{2}{3}\pi\),\(k\in Z\)
Chúc bạn học tốt^^
Đúng 1
Bình luận (0)
Tìm m để các bất phương trình sau đúng với mọi x: (3sinx – 4cosx)2 – 6sinx + 8cosx ≥ 2m - 1 A. m 1 B. m 1 C. m 2 D. m ≤ 0
Đọc tiếp
Tìm m để các bất phương trình sau đúng với mọi x:
(3sinx – 4cosx)2 – 6sinx + 8cosx ≥ 2m - 1
A. m = 1
B. m > 1
C. m > 2
D. m ≤ 0
Đáp án D
Đặt t = 3sin x - 4cos x => -5 ≤ t ≤ 5 (dùng bất đẳng thức bunhiacopxki)
Ta có: y = (3sin x – 4cos x)2 – 6sin x + 8cos x
= t2 – 2t = (t – 2)2 -1
Do -5 ≤ t ≤ 5 => 0 ≤ (t – 2)2 ≤ 36 => min y = -1
Suy ra yêu cầu bài toán -1 ≥ 2m - 1 ⇔ m ≤ 0.
Đúng 0
Bình luận (0)
Giải phương trình:
a, 2sin2x - cos2x = 7sinx + 2cosx - 4
b, sin2x - cos2x + 3sinx - cosx -1 = 0
c, sin2x - 2cos2x + 3sinx - 4cosx + 1 = 0
a) <=> 4sinxcosx -(2cos2x-1)=7sinx+2cosx-4
<=> 2cos2x+(2-4sinx)cosx+7sinx-5=0
- sinx=1 => 2cos2x-2cosx+2=0
pt trên vn
b) <=> 2sinxcosx-1+2sin2x+3sinx-cosx-1=0
<=> cos(2sinx-1)+2sin2x+3sinx-2=0
<=> cosx(2sinx-1)+(2sinx-1)(sinx+2)=0
<=> (2sinx-1)(cosx+sinx+2)=0
<=> sinx=1/2 hoặc cosx+sinx=-2(vn)
<=> x= \(\frac{\pi}{6}+k2\pi\) hoặc \(x=\frac{5\pi}{6}+k2\pi\left(k\in Z\right)\)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
y
3
(
3
sin
x
+
4
cos
x
)
2
+
4
(
3
sin
x
+
4
cos
x
)
+
1
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 3 ( 3 sin x + 4 cos x ) 2 + 4 ( 3 sin x + 4 cos x ) + 1
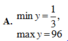
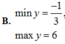
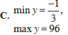
![]()
Tìm m để các bất phương trình
(
3
sin
x
-
4
cos
x
)
2
-
6
sin
x
+
8
cos
x
≥
2
m
-
1
đúng với mọi
x
∈
ℝ
A. m 0 B.
m
≤
0...
Đọc tiếp
Tìm m để các bất phương trình ( 3 sin x - 4 cos x ) 2 - 6 sin x + 8 cos x ≥ 2 m - 1 đúng với mọi x ∈ ℝ
A. m> 0
B. m ≤ 0
C. m < 0
D. m ≤ 1
Xét hàm số y= ( 3sinx – 4cosx )2 – 6sinx + 8cosx
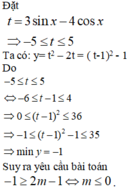
Đáp án B
Đúng 0
Bình luận (0)
Tìm điều kiện của m để phương trình
3
sin
x
+
4
cos
x
m
có nghiệm.
Đọc tiếp
Tìm điều kiện của m để phương trình 3 sin x + 4 cos x = m có nghiệm.
![]()
![]()
![]()
![]()
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
y
3
(
3
s
i
n
x
+
4
c
o
s
x
)
2
+
4
3
sin
x
+
4
cos
x
+
1
A. min y
1...
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 3 ( 3 s i n x + 4 c o s x ) 2 + 4 3 sin x + 4 cos x + 1
A. min y = 1 3 ; max y = 96
B. min y = - 1 3 ; max y = 6
C. min y = - 1 3 ; max y = 96
D. min y = 2; max y = 6