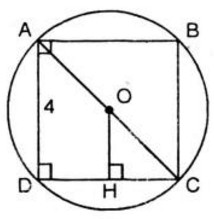
Cho hình vuông ABCD, AB=R, vẽ đường tròn (C;R), từ điểm M trên cạnh AB vẽ tiếp tuyến MH của đường tròn (C) với H là tiếp điểm khác B, tia MH cắt cạnh AD tại N.
a,CMR: AB và AD là 2 tiếp tuyến của (C) và MCN=45 độ
b,CMR: Chu vi tam giác AMN bằng 2R
c, Gọi I là giao điểm của HB với CM, K là giao điểm của HD với CN. CM: CIK=CND
Mình cần ý c









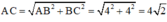 (cm)
(cm)