Chứng minh :a2 + b2 - 2ab ≥ 0

Những câu hỏi liên quan
Chứng minh : a2+b2+c2<2ab+2bc+2ca
Thêm điều kiện: a,b,c thỏa mãn là các cạnh của một tam giác
Ta có: \(a< b+c\)
nên \(a^2< ab+ac\)
Ta có: b<a+c
nên \(b^2< ab+bc\)
Ta có: c<a+b
nên \(c^2< ac+bc\)
Do đó: \(a^2+b^2+c^2< 2\left(ab+bc+ac\right)\)
Đúng 1
Bình luận (0)
chứng minh các đẳng thức sau
(a-b)2=a2-2ab+b2
(a-b)(a+b)=a2-b2
(a+b)3=a3+3a2b+3ab2+b3
(a-b)^2=(a-b)(a-b)=a^2-ab-ab+b^2=a^2-2ba+b^2
(a-b)(a+b)=a^2+ab-ab-b^2=a^2-b^2
(a+3)^3=(a+b)^2*(a+b)
=(a^2+2ab+b^2)(a+b)
=a^3+a^2b+2a^2b+2ab^2+b^2a+b^3
=a^3+3a^2b+3ab^2+b^3
Đúng 1
Bình luận (0)
Câu 6: ( 0,5 điểm)
Chứng minh rằng nếu a, b, c là ba cạnh của một tam giác thì:
a2+ b2+ c2 - 2ab -2bc- 2ac < 0
Vì a,b,c là 3 cạnh tam giác nên \(a+b>c\Leftrightarrow ac+bc>c^2\)
CMTT: \(ab+bc>b^2;ab+ac>a^2\)
Cộng vế theo vế \(\Leftrightarrow a^2+b^2+c^2< ab+bc+ca+ab+bc+ca\)
\(\Leftrightarrow a^2+b^2+c^2< 2ab+2bc+2ca\\ \Leftrightarrow a^2+b^2+c^2-2ab-2bc-2ca< 0\)
Đúng 0
Bình luận (0)
Chứng minh các đẳng thức sau:
a
)
1
−
a
a
1
−
a
+
a
1
−
a
1
−...
Đọc tiếp
Chứng minh các đẳng thức sau:
a ) 1 − a a 1 − a + a 1 − a 1 − a 2 = 1 v ớ i a ≥ 0 v à a ≠ 1 b ) a + b b 2 a 2 b 4 a 2 + 2 a b + b 2 = | a | v ó i a + b > 0 v à b ≠ 0
a) Biến đổi vế trái:
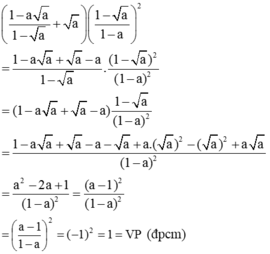
b) Biến đổi vế trái:
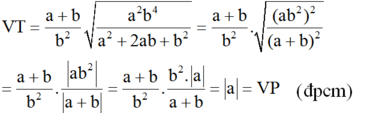
( v ì a + b > 0 n ê n | a + b | = a + b ; b 2 > 0 )
Đúng 0
Bình luận (0)
Chứng tỏ rằng với a và b là các số bất kì thì: a 2 + b 2 - 2 a b ≥ 0
Ta có: a - b 2 ≥ 0 ⇒ a 2 + b 2 - 2 a b ≥ 0
Đúng 0
Bình luận (0)
cho a, b, c là các số thực. Chứng minh rằng: a2 + b2 + c2 ≥ 2ab - 2bc +2ca
BĐT cần chứng minh tương đương:
\(a^2+b^2+c^2\ge2ab-2bc+2ca\)
\(\Leftrightarrow a^2+b^2+c^2+2bc-2a\left(b+c\right)\ge0\)
\(\Leftrightarrow a^2+\left(b+c\right)^2-2a\left(b+c\right)\ge0\)
\(\Leftrightarrow\left(a-b-c\right)^2\ge0\) (luôn đúng)
Vậy BĐT đã cho đúng
Đúng 1
Bình luận (0)
Dùng diện tích để chứng tỏ : a + b 2 = a 2 + 2 a b + b 2
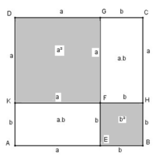
Dựng hình vuông ABCD có cạnh bằng (a + b )
Trên cạnh AB dựng điểm E sao cho AE = a, EB = b, trên cạnh BC dựng điểm H sao cho BH = b, HC = a, trên cạnh CD dựng điểm G sao cho CG = b, GD = a, trên cạnh DA dựng điểm K sao cho DK = a, KA = b, GE cắt KH tại F.
Ta có : diện tích hình vuông ABCD bằng a + b 2
Diện tích hình vuông DKFG bằng a 2
Diện tích hình chữ nhật AKFE bằng a.b
Diện tích hình vuông EBHF bằng b 2
Diện tích hình chữ nhật HCGF bằng a.b
S A B C D = S D K F G + S A K E F + S E B H F + S H C G F
Vậy ta có : a + b 2 = a 2 + 2 a b + b 2
Đúng 0
Bình luận (0)
a2 + b2 -2ab ≥ 0
\(\Leftrightarrow\)\((a-b)^{2}\)\(\ge\)0(luôn đúng)
Đúng 0
Bình luận (0)
\(a^2+b^2-2ab=\left(a-b\right)^2\ge0\) với mọi x
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Dùng diện tích để chứng tỏ :
a
-
b
2
a
2
-
2
a
b
+
b
2
với điều kiện b a
Đọc tiếp
Dùng diện tích để chứng tỏ : a - b 2 = a 2 - 2 a b + b 2 với điều kiện b < a
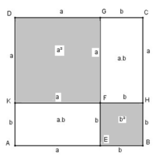
Dựng hình vuông ABCD có cạnh bằng a
Trên cạnh AB lấy điểm E sao cho BE = b
Từ E dựng đường thẳng song song BC cắt CD tại G
Ta có: CG = b, CE = ( a – b ), GD = ( a – b )
Trên cạnh AD lấy điểm K sao cho AK = b
Từ K kẻ đường thẳng song song với AB cắt BC tại H và cắt EG tại F
Ta có: KD = ( a – b ), BH = b
Hình vuông ABCD có diện tích bằng a 2
Hình vuông DKFG có diện tích bằng a - b 2
Hình chữ nhật AEFK có diện tích bằng ( a – b ) b
Hình vuông EBHF có diện tích bằng b 2
Hình chữ nhật HCGF có diện tích bằng ( a – b ).b
S A B C D = S D K F G + S A E F K = S E B H F + S H C G F
nên a - b 2 + a - b b + a - b b + b 2 = a 2
⇒ a - b 2 = a 2 - 2 a b + b 2
Đúng 0
Bình luận (0)
a) Cho m > 0 và m < 1. Chứng minh m 2 < m
b) Cho a > b > 0. Chứng minh a 2 − b 2 > 0 .
a) Ta có M < 1. Mà m > 0 nên m.m < m.1 hay m 2 < m.
b) Từ a > b > 0, ta suy ra được a 2 > ab > b 2 . Sử dụng tính chất bắc cầu và liên hệ giữa thứ tự với phép cộng ta có a 2 - b 2 > 0.
Đúng 0
Bình luận (0)



















