Từ điểm M ở ngoài đường tròn (O) kẻ tiếp tuyến MA, MB với đường tròn. Một đường thẳng (d) cắt đường trong tại C, D (MC<MD). Gọi I là trung điểm của CD. Nối BI cắt đường tròn tại E. CM:
a) MAOB nội tiếp
b) AE//CD
Cho đường tròn (O) và điểm M nằm ngoài đường tròn .Kẻ 2 tiếp tuyến MA , MB với đường tròn (O)
từ điểm A kẻ đường thẳng song song với MB cắt đường tròn tại C ,đường thẳng MC cắt đường tròn tại D
CMR : MD.MC=MA2
Xét ΔMAD và ΔMCA có
góc MAD=góc MCA
góc AMD chung
=>ΔMAD đồng dạng với ΔMCA
=>MA/MC=MD/MA
=>MA^2=MC*MD
cho đường tròn (O) và điểm M nằm ngoài đường tròn .Kẻ 2 tiếp tuyến MA , MB với đường tròn (O)
từ điểm A kẻ đường thẳng song song với MB cắt đường tròn tại C ,đường thẳng MC cắt đường tròn tại D
CMR : đường thẳng AD đi qua trung điểm của MC
Từ một điểm M ở ngoài đường tròn (O) vẽ hai tiếp tuyến MA và MB với đường tròn (A,B là hai tiếp điểm). Qua A vẽ đường thẳng song song với MB và cắt đường tròn tại C ;đoạn thẳng MC cắt đường tròn tại D. Hai đường thẳng AD và MB cắt nhau tại E.
a) CMR: tứ giác MAOB nội tiếp
b) CMR: ∆MED ~ ∆AEM. Từ đó suy ra ME²=ED.AE
c) chứng minh E là trung điểm của đoạn MB
Cho điểm M nằm ngoài đường tròn O,bán kính R.Từ M kẻ hai tiếp tuyến MA,MB với đường tròn O(AB là các tiếp điểm ). Qua A kẻ đường thẳng song song với MB cắt đường tròn (O;R) tại C. Nối MC cắt đường tròn (O;R) tại D. Tia AD cắt MB tại E. Chứng mình:
a. 4 điểm M,A,O,B cùng thuộc một đường tròn
b. EM=EB
giúp mình vs (vẽ hình nữa nha)
a) Xét tứ giác MAOB có
\(\widehat{OAM}\) và \(\widehat{OBM}\) là hai góc đối
\(\widehat{OAM}+\widehat{OBM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: MAOB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Suy ra: M,A,O,B cùng thuộc một đường tròn(đpcm)
cho đường tròn tâm (o) từ điểm M nằm ngoài đường tròn kẻ hai tiếp tuyến MA,MB với đườn tròn (o)(A và B là hai tiếp tuyến).Gọi I là giao điểm của OM và AB; từ B kẻ đườn kính BC của đường tròn(o),đường thẳng MC cắt đường tròn (o) tai D (D khác C)
a)Chứng minh:4 điểm M,A,O,B cùng thuộc một đường tròn
b)Chứng minh:OM vuông với AB và MD.MC=MI.MO
c)Qua O vẽ đường thẳng vuông góc với MC tại E và cắt đường thẳng BA tại F. Chứng minh: FC là tiếp tuyến của đường tròn (O)
cho đường tròn tâm I,đường kinh AC. Từ điểm M nằm ngoài đường tròn kẻ các tiếp tuyến MA,MB (A,B là tiếp điểm ),tiếp tuyến tại C cắt đường thẳng AB tại D. Chứng minh rằng ID vuông góc với MC
Cho đường tròn (O) và một điểm M nằm ngoài đường tròn . Từ M kẻ 2 tiếp tuyến MA;MB ( A;B là tiếp điểm ) . Gọi I là giao điểm của MO và AB .
a) Từ B kẻ đường kính BC của (O) , MC cắt (O) tại D ( D khác C) Chứng minh MD.MC=MI.MO
b) Từ O kẻ đường thẳng vuông góc với MC cắt BA tại F . Chứng minh FC là tiếp tuyến của (O)
a.Vì MA,MB là tiếp tuyến của (O)
→ˆMAO=ˆMBO=90o→MAO^=MBO^=90o
→M,A,O,B→M,A,O,B thuộc đường tròn đường kình OM
b.Vì MA,MBMA,MB là tiếp tuyến của (O)→MO⊥AB=I→MO⊥AB=I
→OA2=OI.OM→OA2=OI.OM
C
Vì OF⊥CM=EOF⊥CM=E
→ˆFAC=ˆFEC=90o→◊AFCE,◊MAEO→FAC^=FEC^=90o→◊AFCE,◊MAEO nội tiếp
→M,A,E,O,B→M,A,E,O,B cùng thuộc một đường tròn
→ˆFCA=ˆFEA=ˆFBO→FCA^=FEA^=FBO^
→FC→FC là tiếp tuyến của (O)
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
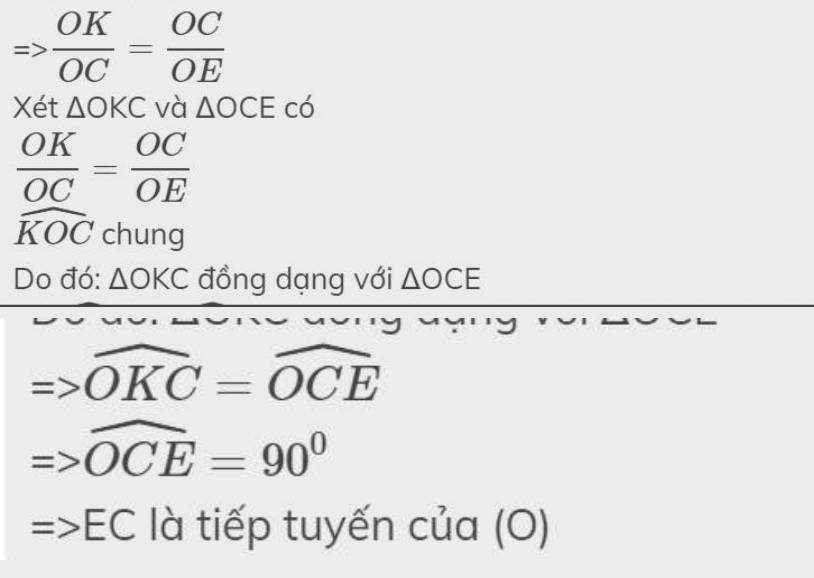
c) Chứng minh EC là tiếp tuyến của (O).
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
c) Chứng minh EC là tiếp tuyến của (O).
giải chi tiết giúp mik vs nhé
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
c) Chứng minh EC là tiếp tuyến của (O).
giúp mik vs ah , mik đang cần gấppppp

b: Xét (O) có
ΔCAB nội tiếp
CB là đường kính
Do đó: ΔCAB vuông tại A
=>CA\(\perp\)AB tại A
=>CA\(\perp\)BE tại A
Ta có: \(\widehat{OAE}=\widehat{OAC}+\widehat{EAC}=\widehat{OAC}+90^0\)
\(\widehat{MAC}=\widehat{MAO}+\widehat{OAC}=\widehat{OAC}+90^0\)
Do đó: \(\widehat{OAE}=\widehat{MAC}\)
Xét tứ giác CKAE có \(\widehat{CKE}=\widehat{CAE}=90^0\)
nên CKAE là tứ giác nội tiếp
=>\(\widehat{ACK}=\widehat{AEK}\)
=>\(\widehat{ACM}=\widehat{AEO}\)
Xét ΔAMC và ΔAOE có
\(\widehat{ACM}=\widehat{AEO}\)
\(\widehat{MAC}=\widehat{OAE}\)
Do đó: ΔAMC đồng dạng với ΔAOE
=>\(\dfrac{AM}{AO}=\dfrac{AC}{AE}\)
=>\(AM\cdot AE=AO\cdot AC\)