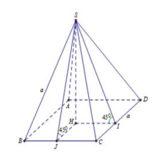
Cho hình lập phương ABCD.A'B'C'D' cạnh a, M \(\in\) BC', N \(\in\) AB'. MN tạo với mặt đáy ABCD một góc \(\alpha\) . CMR: MN \(\ge\) $\dfrac{a}{\sqrt{2}\cos{\(\alpha\)}+\sin{\(\alpha\)}}$

Những câu hỏi liên quan
Cho hình chóp ABCD có đáy ABCD là cạnh a,hình chiếu vuông góc của S lên mặt đáy là trung điểm M của cạnh AB,SMfrac{asqrt{3}}{2}.Gọi N,Q lần lượt là trung điểm của SC,DC.
a/ CMR BC vuông góc với mp SAB
b/CM mp SDC vuông với mp SMQ
c/Xác định và tính cos của góc giữa hai mp ABN và SDC
Mn gỉải hộ mình câu 4C với ,mình cần gấp ạ.Cảm ơn mn nhiều
Đọc tiếp
Cho hình chóp ABCD có đáy ABCD là cạnh a,hình chiếu vuông góc của S lên mặt đáy là trung điểm M của cạnh AB,SM=\(\frac{a\sqrt{3}}{2}\).Gọi N,Q lần lượt là trung điểm của SC,DC.
a/ CMR BC vuông góc với mp SAB
b/CM mp SDC vuông với mp SMQ
c/Xác định và tính cos của góc giữa hai mp ABN và SDC
Mn gỉải hộ mình câu 4C với ,mình cần gấp ạ.Cảm ơn mn nhiều
Đáy ABCD là hình gì cạnh a bạn? Hình vuông hay hình thoi?
Đúng 0
Bình luận (1)
Hình chắc bạn có rồi nên ko cần vẽ nữa
Qua N kẻ đường thẳng song song CD cắt SD tại E \(\Rightarrow NE//AB\Rightarrow E\in\left(ABN\right)\)
Nối SQ cắt NE tại F \(\Rightarrow SQ\perp NE\) (do \(SQ\perp CD\)) (1)
\(AB\perp SM\Rightarrow NE\perp SM\) (do \(NE//AB\) ) (2)
(1);(2) \(\Rightarrow NE\perp\left(SMQ\right)\Rightarrow\left(ABNE\right)\perp\left(SMQ\right)\)
Lại có \(\left(SMQ\right)\perp\left(SCD\right)\Rightarrow\widehat{SFM}\) là góc giữa (ABN) và (SCD)
Đến đoạn tính toán:
\(SQ=\sqrt{SM^2+MQ^2}=...\) (MQ=BC=a)
\(\Rightarrow SF=\frac{1}{2}SQ=...\)
Gọi O là tâm đáy \(\Rightarrow OF=\frac{1}{2}SM=...\) (t/c đường trung bình)
\(\Rightarrow MF=\sqrt{OF^2+OM^2}=...\) (\(OM=\frac{1}{2}BC=...\))
Áp dụng định lý hàm cos:
\(cos\widehat{SFM}=\frac{SF^2+MF^2-SM^2}{2SF.MF}=...\)
Đúng 0
Bình luận (2)
Cho hình chóp tứ giác đều SABCD có đáy ABCD là hình vuông cạnh bằng a, mặt bên hợp với mặt đáy góc 60 độ. Gọi M,N là trung điểm các cạnh AB và SD. Tính theo a thể tích của khối chóp SABCD và khoảng cách giữa MN,CD.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a (a 0). Hai mặt phẳng (SBC) và (SCD) cùng tạo với mặt phẳng (ABCD) một góc
45
∘
. Biết SB a và hình chiếu của S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính thể tích khối chóp S.ABCD
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a (a > 0). Hai mặt phẳng (SBC) và (SCD) cùng tạo với mặt phẳng (ABCD) một góc 45 ∘ . Biết SB = a và hình chiếu của S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính thể tích khối chóp S.ABCD
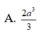
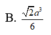


Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a
a
0
. Hai mặt phẳng (SBC) và
S
C
D
cùng tạo với mặt phẳng (ABCD) một góc
45
°
. Biết
S
B
a
và hình chiếu của S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính thể tí...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a a > 0 . Hai mặt phẳng (SBC) và S C D cùng tạo với mặt phẳng (ABCD) một góc 45 ° . Biết S B = a và hình chiếu của S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính thể tích khối chóp S.ABCD
A. 2 a 3 3
B. 2 a 3 6
C. a 3 4
D. 2 a 3 9
Cho \(\alpha\) , \(\beta\in\left(0;\dfrac{\pi}{2}\right)\) và sin \(\alpha\) = \(\dfrac{1}{\sqrt{5}}\) ; Cos \(\alpha\) = \(\dfrac{1}{\sqrt{10}}\) . Tính Cos \(\left(\alpha+\beta\right)\)
Kiểm tra lại đề bài, \(cosa=\dfrac{1}{\sqrt{10}}\) hay \(cos\beta=\dfrac{1}{\sqrt{10}}\)?
Đúng 0
Bình luận (1)
a) Cho $\cos \alpha=\dfrac{3}{4}$ với $0^{\circ}<\alpha<90^{\circ}$. Tính $A=\dfrac{\tan \alpha+3 \cot \alpha}{\tan \alpha+\cot \alpha}$.
b) Cho $\tan \alpha=\sqrt{2}$. Tính $B=\dfrac{\sin \alpha-\cos \alpha}{\sin ^{3} \alpha+3 \cos ^{3} \alpha+2 \sin \alpha}$.
Cho \(\sin\alpha+\cos\alpha=\frac{\sqrt{6}}{2},a\in\left(0;\frac{\pi}{4}\right)\)
Tính giá trị biểu thức: \(P=\cos\left(\alpha+\frac{\pi}{4}\right)+\sqrt{2\left(1-\sin\alpha\cos\alpha+\sin\alpha-\cos\alpha\right)}\)
\(F=\dfrac{\sin\alpha-2\sin\left(2\alpha\right)+\sin\left(3\alpha\right)}{\cos\alpha-3\cos\left(2\alpha\right)+\cos\left(3\alpha\right)}\)
Mn rút gọn giùm mình biểu thức này với. Mình cảm ơn ạ :<
Mẫu số là \(-3cos2a\) hay \(-2cos2a\) vậy bạn? -3 không hợp lý
Đúng 0
Bình luận (0)
1/ Cho \(cot\alpha=\sqrt{5}\) . Tính \(C=sin^2\alpha-sin\alpha cos\alpha+cos^2\alpha\)
2/ Cho \(tan\alpha=3\) . Tính \(B=\dfrac{sin\alpha-cos\alpha}{sin^3\alpha+3cos^3\alpha+2sin\alpha}\)
1) \(cot\alpha=\sqrt[]{5}\Rightarrow tan\alpha=\dfrac{1}{\sqrt[]{5}}\)
\(C=sin^2\alpha-sin\alpha.cos\alpha+cos^2\alpha\)
\(\Leftrightarrow C=\dfrac{1}{cos^2\alpha}\left(tan^2\alpha-tan\alpha+1\right)\)
\(\Leftrightarrow C=\left(1+tan^2\alpha\right)\left(tan^2\alpha-tan\alpha+1\right)\)
\(\Leftrightarrow C=\left(1+\dfrac{1}{5}\right)\left(\dfrac{1}{5}-\dfrac{1}{\sqrt[]{5}}+1\right)\)
\(\Leftrightarrow C=\dfrac{6}{5}\left(\dfrac{6}{5}-\dfrac{\sqrt[]{5}}{5}\right)=\dfrac{6}{25}\left(6-\sqrt[]{5}\right)\)
Đúng 1
Bình luận (0)
1: \(cota=\sqrt{5}\)
=>\(cosa=\sqrt{5}\cdot sina\)
\(1+cot^2a=\dfrac{1}{sin^2a}\)
=>\(\dfrac{1}{sin^2a}=1+5=6\)
=>\(sin^2a=\dfrac{1}{6}\)
\(C=sin^2a-sina\cdot\sqrt{5}\cdot sina+\left(\sqrt{5}\cdot sina\right)^2\)
\(=sin^2a\left(1-\sqrt{5}+5\right)=\dfrac{1}{6}\cdot\left(6-\sqrt{5}\right)\)
2: tan a=3
=>sin a=3*cosa
\(1+tan^2a=\dfrac{1}{cos^2a}\)
=>\(\dfrac{1}{cos^2a}=1+9=10\)
=>\(cos^2a=\dfrac{1}{10}\)
\(B=\dfrac{3\cdot cosa-cosa}{27\cdot cos^3a+3\cdot cos^3a+2\cdot3\cdot cosa}\)
\(=\dfrac{2\cdot cosa}{30cos^3a+6cosa}=\dfrac{2}{30cos^2a+6}\)
\(=\dfrac{2}{3+6}=\dfrac{2}{9}\)
Đúng 1
Bình luận (0)