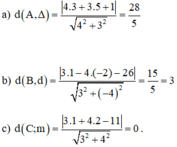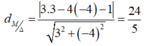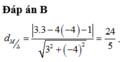Tìm M thuộc Oy sao khoảng cách từ M đến Δ: 3x+4y-6=0 bằng \(\frac{7}{5}\)

Những câu hỏi liên quan
Tìm khoảng cách từ một điểm đến đường thẳng trong các trường hợp sau:
a, A(3; 5) và Δ : 4x + 3y +1 = 0
b, B(1; -2) và d: 3x – 4y -26 = 0
c, C(1; 2) và m: 3x + 4y -11 = 0
Cho M(2;5) và đường thẳng delta : 3x+4y-m=0 . Tìm m sao cho khoảng cách từ M đến đường thẳng delta bằng 1
\(d\left(M;\Delta\right)=\dfrac{\left|3.2+4.5-m\right|}{\sqrt{3^2+4^2}}=1\)
\(\Leftrightarrow\left|26-m\right|=5\Rightarrow\left[{}\begin{matrix}m=21\\m=31\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho đường thẳng d: y=x-5
a) Tìm các điểm M thuộc trục Ox sao cho khoảng cách từ M đến đường thẳng d bằng 2.
b) Tìm các điểm N thuộc trục Oy sao cho khoảng cách từ N đến đường thẳng d bằng 2.
cho đường thẳng Δ : x + y - 2 = 0 và điểm A( 2; 2). Tìm tọa độ điểm M thuộc đường thẳng Δ sao cho khoảng cách từ A đến M nhỏ nhất.
Khoảng cách AM là nhỏ nhất khi và chỉ khi M là hình chiếu vuông góc của A lên \(\Delta\)
Gọi d là đường thẳng qua A và vuông góc \(\Delta\Rightarrow\) d nhận \(\left(1;-1\right)\) là 1 vtpt
Phương trình d:
\(1\left(x-2\right)-1\left(y-2\right)=0\Leftrightarrow x-y=0\)
M là giao điểm của d và \(\Delta\) nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x+y-2=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\) \(\Rightarrow M\left(1;1\right)\)
Đúng 1
Bình luận (0)
Khoảng cách từ điểm M (3;-4) đến đường thẳng
△
:
3
x
-
4
y
-
1
0
bằng A.
8
5
B.
24
5
C.
5
D.
7
5
Đọc tiếp
Khoảng cách từ điểm M (3;-4) đến đường thẳng △ : 3 x - 4 y - 1 = 0 bằng
A. 8 5
B. 24 5
C. 5
D. 7 5
Khoảng cách từ điểm M(3;-4) đến đường thẳng D: 3x-4y-1=0 bằng
A. 8 5
B. 24 5
C. 5
D. 7 5
Khoảng cách từ điểm M(1;-1) đến đường thẳng Δ: 3x + y + 4 = 0 là:
A. 2 10
B. 3 10 5
C. 5 2
D. 1
Chọn B.
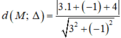
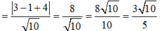
Vậy khoảng cách từ điểm M(1;-1) đến đường thẳng Δ: 3x + y + 4 = 0 là 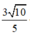
Đúng 0
Bình luận (0)
Trong không gian Oxyz, đường thẳng Δ qua điểm A(2;1;5) và song song với mặt phẳng (P):3x-y-z+30 sao cho khoảng cách từ điểm M(1;2;−1) đến đường thẳng Δ nhỏ nhất, biết
u
⇀
a
;
1
;
b
là một véctơ chỉ phương của đường thẳng Δ. Giá trị của a+b bằng A.
-
81
13
B.
-...
Đọc tiếp
Trong không gian Oxyz, đường thẳng Δ qua điểm A(2;1;5) và song song với mặt phẳng (P):3x-y-z+3=0 sao cho khoảng cách từ điểm M(1;2;−1) đến đường thẳng Δ nhỏ nhất, biết u ⇀ a ; 1 ; b là một véctơ chỉ phương của đường thẳng Δ. Giá trị của a+b bằng
A. - 81 13
B. - 9 4
C. 9 4
D. 81 13
Vì 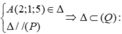
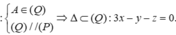
Gọi
![]()
![]()
![]()
Dấu bằng đạt tại
![]()
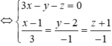
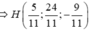
Vì vậy
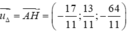
![]()
![]()
Chọn đáp án A.
Đúng 0
Bình luận (0)
Một (E) có độ dài trục lớn bằng 6, tâm sai bằng \(\dfrac{1}{2}\), khoảng cách từ M thuộc (E) đến tiêu điểm F1 (có hoành độ âm) bằng 7.
a. Tìm khoảng cách từ M đến F2
b. Viết PTCT (E) và tìm M