cho hình vuông ABCD có cạnh bằng a ,M là 1 điểm di động trên cạnh BC(M khác B và C),tia AM cắt DC tại E .Trên tia đối của tia DC lấy N sao cho DN=BM,tia NA cắt CB tại F chứng minh:BM.DE=DN.BF=\(^{a^2}\)

Những câu hỏi liên quan
Cho hình vuông abcd, trên cạnh bc lấy M (M khác B, M khác C). Tia AM cắt tia DC tại E, trên tia DC lấy điểm N sao cho ND = BM. a) C/m tam giác AMN là tam giác vuông cân. b) tia NA cắt đường thẳng CB tại P, đoạn thẳng MN cắt AD tại I. Từ A vẽ đường thẳng vuông góc với MN tại H và cắt cạnh CD tại K. C/m: tam giác ADK đồng dạng tam giác MHK. c) C/m: NDxNE=NCxNK.
Cho hình vuông ABCD cố định, M là 1 điểm lấy trên cạnh BC (M B). Tia AM cắt DC tại P. Trên tia đối của tia DC lấy điểm N sao cho DN BM. a. Chứng minh: AND ABM và MAN là vuông cân.b. Chứng minh: ABM và PDA đồng dạng và BC2 BM . DP. c. Qua A vẽ đường thẳng vuông góc với MN tại H và cắt CD tại Q, MN cắt AD ở I. Chứng minh: AH . AQ AI . AD và DÂQ HMQ.d. Chứng minh: NDH và NIQ đồng dạng
Đọc tiếp
Cho hình vuông ABCD cố định, M là 1 điểm lấy trên cạnh BC (M B). Tia AM cắt DC tại P. Trên tia đối của tia DC lấy điểm N sao cho DN = BM.
a. Chứng minh: AND = ABM và MAN là vuông cân.
b. Chứng minh: ABM và PDA đồng dạng và BC2 = BM . DP.
c. Qua A vẽ đường thẳng vuông góc với MN tại H và cắt CD tại Q, MN cắt AD ở I. Chứng minh: AH . AQ = AI . AD và DÂQ = HMQ.
d. Chứng minh: NDH và NIQ đồng dạng
cho hình vuông ABCD có cạnh bằng a ,M là 1 điểm di động trên cạnh BC(M khác B và C),tia AM cắt DC tại E .Trên tia đối của tia DC lấy N sao cho DN=BM,tia NA cắt CB tại F.Chứng minh:tam giác AMN vuông cân
Xét Δ ABM và Δ ADN có:
BM = DN (gt)
\(\widehat{ABC}\)= \(\widehat{ADN}=90^0\) ( góc ADN kề bù với góc ADE ( E∈DC)
AB = AD ( ABCD là hình vuông)
=> Δ ABM = Δ ADN ( c-g-c)
=> AM = AN ( hai cạnh tương ứng )
=> Δ NAM cân tại A
Xét Δ ANH và Δ AMH có:
AM = AN (cmt)
AH cạnh chung
\(\widehat{AHN}=\widehat{AHM}=90^0\)
=> Δ AHN = ΔAHM ( cạnh huyền - cạnh góc vuông)
=> HN = HM ( hai cạnh tương ứng )
Xét Δ cân NAM có:
AH vừa là đường cao vừa là đường trung tuyến
=> ΔNAM vuông cân tại A.
Đúng 0
Bình luận (0)
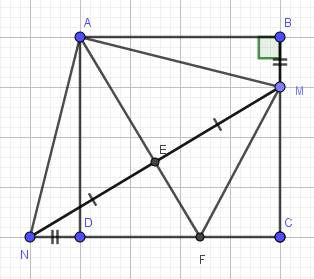
Bài 1. Cho hình vuông ABCD có cạnh bằng a. Trên cạnh BC lấy điểm M, trên tia đối của tia DC lấy điểm N sao cho BM = DN. a) Chứng minh tam giác AMN là tam giác vuông cân. b) Gọi E là trung điểm của MN. Tia AE cắt CD tại F. Chứng minh tam giác FAN = tam giác FAM.
a) Do ABCD là hình vuông (gt)
\(\Rightarrow AB=AD\)
\(\widehat{ABM}=\widehat{ADN}=90^0\)
Xét hai tam giác vuông: \(\Delta ABM\) và \(\Delta ADN\) có:
\(AB=AD\left(cmt\right)\)
\(BM=DN\left(gt\right)\)
\(\Rightarrow\Delta ABM=\Delta ADN\) (hai cạnh góc vuông)
\(\Rightarrow AM=AN\) (hai cạnh tương ứng)
\(\widehat{BAM}=\widehat{DAN}\) (hai góc tương ứng)
Ta có:
\(\widehat{BAM}+\widehat{DAM}=90^0\)
\(\Rightarrow\widehat{DAN}+\widehat{DAM}=90^0\)
\(\Rightarrow\widehat{MAN}=90^0\)
\(\Delta AMN\) có:
\(AM=AN\left(cmt\right)\)
\(\Rightarrow\Delta AMN\) cân tại A
Mà \(\widehat{MAN}=90^0\left(cmt\right)\)
\(\Rightarrow\Delta AMN\) vuông cân tại A
b) Do \(\Delta AMN\) cân tại A
E là trung điểm của MN
\(\Rightarrow AE\) là đường trung tuyến, cũng là đường cao của \(\Delta AMN\)
\(\Rightarrow AE\perp MN\)
\(\Rightarrow EF\perp MN\)
Xét hai tam giác vuông: \(\Delta FEM\) và \(\Delta FEN\) có:
\(EM=EN\left(gt\right)\)
\(EF\) là cạnh chung
\(\Rightarrow\Delta FEM=\Delta FEN\) (hai cạnh góc vuông)
\(\Rightarrow FM=FN\) (hai cạnh tương ứng)
Xét \(\Delta FAN\) và \(\Delta FAM\) có:
\(FA\) là cạnh chung
\(FN=FM\left(cmt\right)\)
\(AN=AM\left(cmt\right)\)
\(\Rightarrow\Delta FAN=\Delta FAM\left(c-c-c\right)\)
Đúng 3
Bình luận (0)
Cho hình vuông ABCD nhất định M là 1 điểm lấy trên cạnh BC tia AM cắt DC tại P trên tia đối tia DC lấy điểm N sao cho DN=BM
Chứng minh tam giác AND=ABM và tam giác MAN vuông cân
Chứng minh tam giác ABM và tam giác PAD đồng dạng và BC^2=BM.DP
Qua A vẽ đường thẳng vuông góc với MN tại H và cắt CD tại Q ,MN cắt AD ở I chứng minh AH.AQ=AI.AD và góc DAQ=HMQ
a: Xét ΔAND và ΔABM có
góc A chung
AN=DM
AB=AD
=>ΔAND=ΔABM
=>AN=AM
góc NAD=góc BAM
=>góc NAD+góc DAM=góc DAM+góc BAM=90 độ
=>góc NAM=90 độ
=>ΔNAM vuông cân tại A
b: Xét ΔABM và ΔPDA có
góc B=góc D
góc BAM=góc APD
=>ΔABM đồng dạng với ΔPDA
=>AB/BM=PD/AD
=>AB*AD=BM*PD=BC^2
c: Xét ΔAIH và ΔAQD có
góc A chung
góc H=góc D
=>ΔAIH đồng dạng với ΔAQD
=>AI*AD=AH*AQ
Đúng 1
Bình luận (0)
cho hình vuông ABCD có cạnh bằng a. Trên BC là M, trên tia đối của tia DC lấy N sao cho BM=DN. Vẽ AH vuông góc với NM (H thuộc NM), AH cắt DC tại E. Gọi G là giao điểm của MN với AD. a. Chứng minh tam giác NAM vuông cân và D,H,B thẳng hàng.
Mọi Người giúp em chi tiết với ạ Cho hình vuông ABCD cạnh a. Lấy điểm M bất kì trên BC. Trên tia đối của tia DC lấy điểm N sao cho DNBM.a ) Chứng minh ANAM.b ) Kẻ AI MN tại I, tia AI cắt DC tại F. Lấy E đối xứng với F qua I. Chứng minh NEMF là hình thoic ) Đường vuông góc với AM tại M cắt đường vuông góc với AN tại N ở H. Chứng minh : AN AM và ba điểm A, I, H thẳng hàng.d ) Chứng minh rằng khi M thay đổi vị trí trên BC thì chu vi tam giác MFC luôn không đổi.
Đọc tiếp
Mọi Người giúp em chi tiết với ạ
Cho hình vuông ABCD cạnh a. Lấy điểm M bất kì trên BC. Trên tia đối của tia DC lấy điểm N sao cho DN=BM.
a ) Chứng minh AN=AM.
b ) Kẻ AI MN tại I, tia AI cắt DC tại F. Lấy E đối xứng với F qua I. Chứng minh NEMF là hình thoi
c ) Đường vuông góc với AM tại M cắt đường vuông góc với AN tại N ở H. Chứng minh : AN= AM và ba điểm A, I, H thẳng hàng.
d ) Chứng minh rằng khi M thay đổi vị trí trên BC thì chu vi tam giác MFC luôn không đổi.
Cho hình vuông ABCD cố định. Một điểm I di động trên cạnh AB (I khác A và B). Tia DI cắt đường thẳng CB tại E. Đường thẳng CI cắt AE tại M. Đường thẳng BM cắt đường thẳng DE tại F.1. Chứng minh rằng BI^2/BE^2 AI/CE.2. Trên tia đối của tia AB lấy điểm P sao cho AP BE. Đường thẳng AE cắt CP tại H. Chứng minh rằng DH song song CI.3. Tìm quỹ tích điểm F khi I di động trên cạnh AB.
Đọc tiếp
Cho hình vuông ABCD cố định. Một điểm I di động trên cạnh AB (I khác A và B). Tia DI cắt đường thẳng CB tại E. Đường thẳng CI cắt AE tại M. Đường thẳng BM cắt đường thẳng DE tại F.
1. Chứng minh rằng BI^2/BE^2 = AI/CE.
2. Trên tia đối của tia AB lấy điểm P sao cho AP = BE. Đường thẳng AE cắt CP tại H. Chứng minh rằng DH song song CI.
3. Tìm quỹ tích điểm F khi I di động trên cạnh AB.
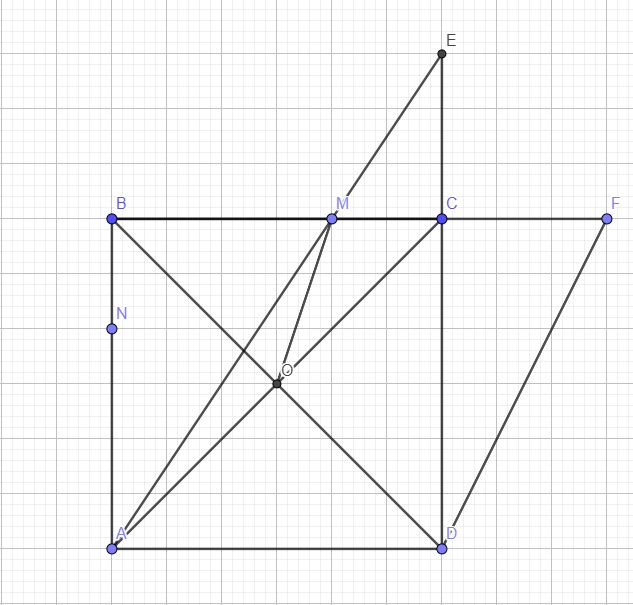
Cho hình vuông ABCD . Trên cạnh BC lấy điểm M (khác B và C) . Trên cạnh AB lấy điểm N sao cho: BN CM . Đường thẳng AM cắt CD tại E .Trên tia đối của tia CB lấy điểm F sao cho CF CE. Gọi O là giao điểm của AC và BD .Chứng minh hai tam giác BOM và BFD đồng dạng.
Đọc tiếp
Cho hình vuông ABCD . Trên cạnh BC lấy điểm M (khác B và C) . Trên cạnh AB lấy điểm N sao cho: BN = CM . Đường thẳng AM cắt CD tại E .Trên tia đối của tia CB lấy điểm F sao cho CF = CE. Gọi O là giao điểm của AC và BD .
Chứng minh hai tam giác BOM và BFD đồng dạng.
Đặt cạnh hình vuông là a, ta có \(BD=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(\Rightarrow BO=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}\Rightarrow BO.BD=a^2\)
Xét 2 tam giác vuông AED và MAB có:
\(\left\{{}\begin{matrix}\widehat{ADE}=\widehat{MBA}=90^0\\\widehat{AED}=\widehat{MAB}\left(slt\right)\end{matrix}\right.\) \(\Rightarrow\Delta AED\sim\Delta MAB\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{BM}=\dfrac{ED}{AB}\Rightarrow BM.ED=AD.AB=a^2\)
\(\Rightarrow BM.ED=BO.BD\)
Mà \(ED=BF\) (do \(BC=CD\) và \(CE=CF\))
\(\Rightarrow BM.BF=BO.BD\Rightarrow\dfrac{BM}{BD}=\dfrac{BO}{BF}\)
Xét hai tam giác BOM và BFD có:
\(\left\{{}\begin{matrix}\dfrac{BM}{BD}=\dfrac{BO}{BF}\\\widehat{OBM}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta BOM\sim\Delta BFD\left(c.g.c\right)\)
Đúng 2
Bình luận (2)