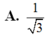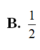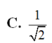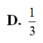Cho hình chóp đều SABCD các cạnh điều bằng a.
a) Tính góc giữa cạnh bên và mặt đáy.
b) Tính góc giữa mặt bên và mặt đáy.
GIÚP EM VỚI Ạ !!
cho hình chóp SABCD đều cạnh đáy a, góc giữa mặt bên và đáy bằng 45°. Tính khoảng cách từ A đến (SBD)
Bạn kiểm tra lại đề, chắc là đề đúng chứ? (SBD) hay (SBC)?
Nếu đề đúng thế này thì gọi O là tâm đáy
Vì \(AC\perp BD\Rightarrow AO\perp\left(SBD\right)\Rightarrow AO=d\left(A;\left(SBD\right)\right)\)
\(AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
Cho hình chóp đều SABCD có cạnh đáy bằng 2a,góc giữa cạnh bên và mặt phẳng đáy bằng 45°.Tính độ dài đường cao hình chóp đã cho
(SA;(ABCD))=45 độ
=>(AS;(AO)=45 độ
=>góc SAO=45 độ
AC=2a*căn 2
=>AO=a*căn 2
=>SO=a*căn 2
Cho hình chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b.
a) Tính sin của góc tạo bởi cạnh bên và mặt đáy.
b) Tính tang của góc giữa mặt phẳng chứa mặt đáy và mặt phẳng chứa mặt bên.
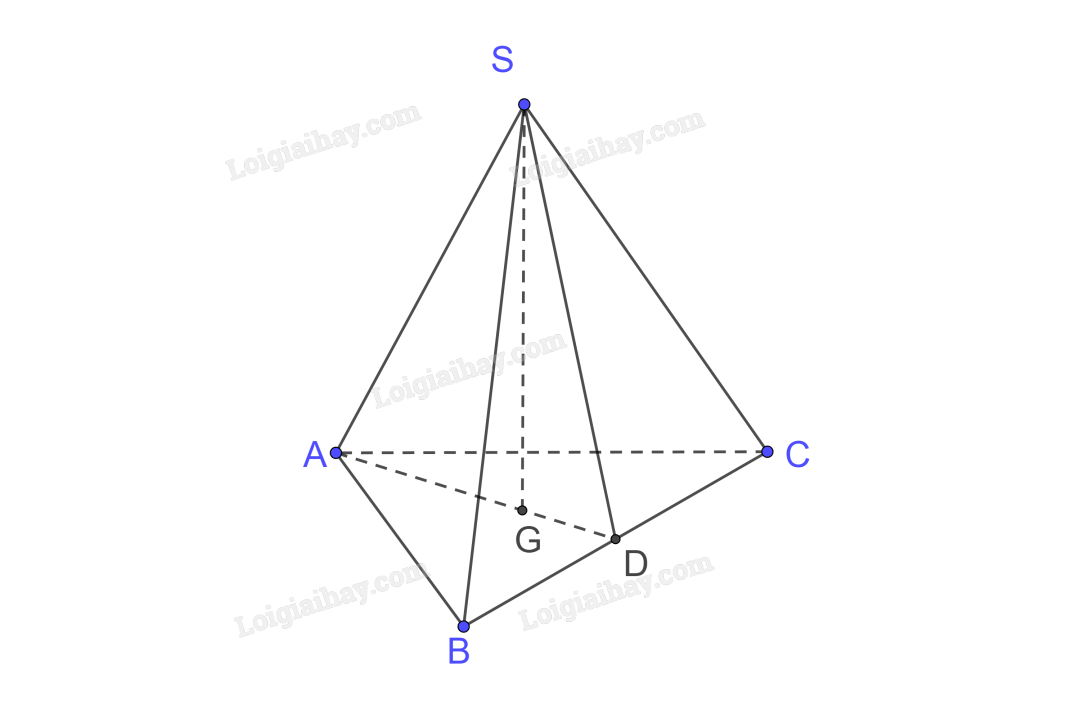
Vì hình chóp S.ABC đều, gọi G là hình chiếu của S trên (ABC) nên G là tâm của đáy ABC là tam giác đều do đó G cũng là trọng tâm hay trực tâm của tam giác ABC.
Gọi AG cắt BC tại D
a) Ta có A là hình chiếu của A trên (ABC)
G là hình chiếu của S trên (ABC)
\( \Rightarrow \) AG là hình chiếu của SA trên (ABC)
\( \Rightarrow \left( {SA,\left( {ABC} \right)} \right) = \left( {SA,AG} \right) = \widehat {SAG}\)
Tam giác ABC đều cạnh a nên \(AD = \frac{{a\sqrt 3 }}{2}\)
Mà G là trọng tâm nên \(AG = \frac{2}{3}AD = \frac{{a\sqrt 3 }}{3}\)
Xét tam giác SAG vuông tại G có
\(SG = \sqrt {S{A^2} - A{G^2}} = \sqrt {{b^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} \)
\(\sin \widehat {SAG} = \frac{{SG}}{{SA}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} :b = \sqrt {1 - \frac{{{a^2}}}{{3{b^2}}}} \)
b) Ta có \(AG \bot BC,SG \bot BC \Rightarrow BC \bot \left( {SAD} \right);SD \subset \left( {SAD} \right) \Rightarrow BC \bot SD\)
\(BC \bot AD\) (G là trực tâm)
\(\begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\ \Rightarrow \left( {\left( {SBC} \right),\left( {ABC} \right)} \right) = \left( {AD,SD} \right) = \widehat {SDA}\end{array}\)
Mà G là trọng tâm nên \(GD = \frac{1}{3}AD = \frac{{a\sqrt 3 }}{6}\)
Xét tam giác SGD vuông tại G có
\(\tan \widehat {SGD} = \frac{{SG}}{{GD}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} :\frac{{a\sqrt 3 }}{6} = \frac{6}{{a\sqrt 3 }}.\sqrt {{b^2} - \frac{{{a^2}}}{3}} \)
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa cạnh bên với mặt phẳng đáy bằng ∝
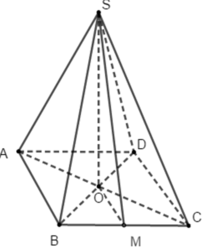
Tan của góc giữa mặt bên và mặt đáy bằng:
A. tan α
B. c o t α
C. 2 tan α
D. 2 2 tan α
Chân đường cao hình chóp đều S.ABCD trùng với tâm O của đáy ABCD. AO là hình chiếu của SA lên (ABCD)
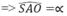
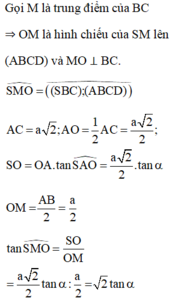
Đáp án C
Cho hình chóp tam giác đều có góc giữa cạnh bên và mặt đáy bằng 45 0 . Tính sin góc giữa mặt bên và mặt đáy.
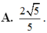
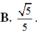
![]()
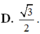
Cho hình chóp SABCD đều. Cạnh đáy a, góc giữa mặt bên và đáy bằng 45°. Tính khoảng cách từ a)A đến (SBD) b)O đến (SAB) c)CD đến (SAB)
Cho hình chóp đều S.ABC có cạnh đáy bằng a, góc giữa mặt bên và mặt đáy bằng \(60^o\). Tính độ dài cạnh bên?
Gọi O là tâm đáy, M là trung điểm AB
Ta có: \(\left\{{}\begin{matrix}SO\perp\left(ABC\right)\\OM\perp AB\end{matrix}\right.\) \(\Rightarrow\widehat{SMO}\) hay là góc giữa mặt bên và mặt đáy
\(\Rightarrow\widehat{SMO}=60^0\) \(\Rightarrow SO=OM.tan60^0=\dfrac{1}{3}CM.tan60^0=\dfrac{1}{3}AB.\dfrac{\sqrt{3}}{2}.tan60^0=\dfrac{a}{2}\)
\(CO=\dfrac{2}{3}CM=\dfrac{2}{3}.AB\dfrac{\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
\(SC=\sqrt{SO^2+OC^2}=\dfrac{a\sqrt{21}}{6}\)
Cho hình chóp tứ giác đều SABCD có cạnh đáy là a góc giữa mặt bên với mặt đáy là 60° tính khoảng cách giữa hai đường thẳng CM và SA biết M là trung điểm của SD
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính côsin của góc giữa mặt bên và mặt đáy.