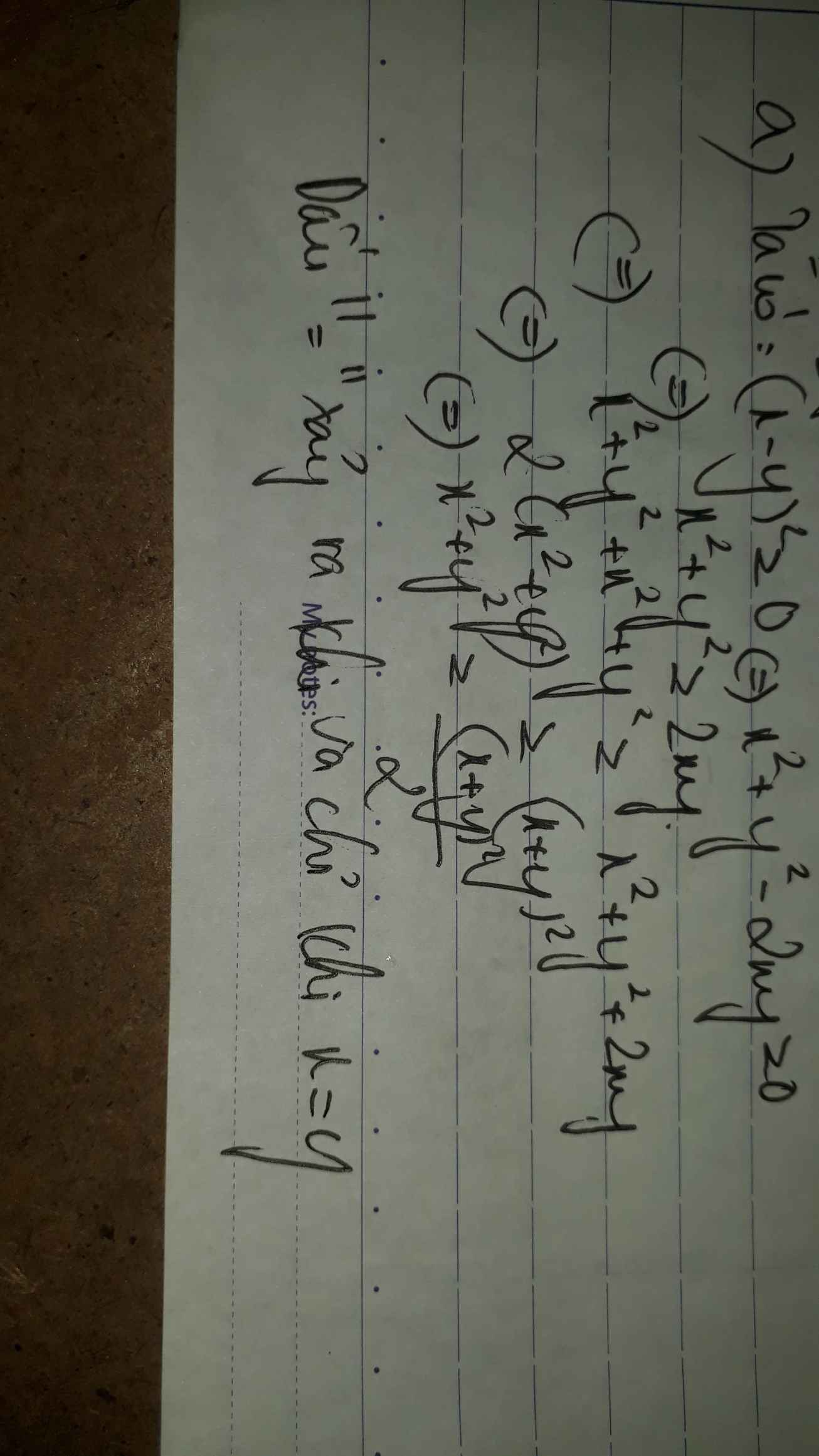Chứng minh BĐT \(2\left(x^2+y^2\right)\ge\left(x+y\right)^2\)

Những câu hỏi liên quan
ta có bđt cần chứng minh frac{sqrt{xy+z}+sqrt{2x^2+2y^2}}{1+sqrt{xy}}ge1Leftrightarrowsqrt{xy+z}+sqrt{2left(x^2+y^2right)}ge1+sqrt{xy}Áp dụng bđt bu nhi ta có sqrt{2left(x^2+y^2right)}ge x+y (1)mà x+y+z1Rightarrow xy+zxy+zleft(x+y+zright)left(z+xright)left(z+yright)áp dụng bu nhi a ta có sqrt{left(z+xright)left(z+yright)}ge z+sqrt{xy} (2)từ (1) và (2) sqrt{xy+z}+sqrt{2x^2+2y^2}ge x+y+z+sqrt{xy}1+sqrt{xy}
Đọc tiếp
ta có bđt cần chứng minh
\(\frac{\sqrt{xy+z}+\sqrt{2x^2+2y^2}}{1+\sqrt{xy}}\ge1\Leftrightarrow\sqrt{xy+z}+\sqrt{2\left(x^2+y^2\right)}\ge1+\sqrt{xy}\)
Áp dụng bđt bu nhi ta có
\(\sqrt{2\left(x^2+y^2\right)}\ge x+y\) (1)
mà x+y+z=1\(\Rightarrow xy+z=xy+z\left(x+y+z\right)=\left(z+x\right)\left(z+y\right)\)
áp dụng bu nhi a ta có \(\sqrt{\left(z+x\right)\left(z+y\right)}\ge z+\sqrt{xy}\) (2)
từ (1) và (2) => \(\sqrt{xy+z}+\sqrt{2x^2+2y^2}\ge x+y+z+\sqrt{xy}=1+\sqrt{xy}\)
Cho các số dương x,y,z . Chứng minh BĐT :
\(\frac{\left(x+1\right)\left(y+1\right)^2}{3\sqrt[3]{z^2x^2}+1}+\frac{\left(y+1\right)\left(z+1\right)^2}{3\sqrt[3]{x^2y^2}+1}+\frac{\left(z+1\right)\left(x+1\right)^2}{3\sqrt[3]{y^2z^2}+1}\ge x+y+z+3\)
ko bt lm thi đừng CMT tầm bậy nhé !
bài lớp 10 bất đẳng thức mấy chú k hiểu là đúng r -______-''
Đúng 0
Bình luận (0)
hc o nha cho đó mk dg hc chi vaxma tốc độ
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
ta có:(vế phải)2le3left(frac{x^3}{y+z}+frac{y^3}{z+x}+frac{z^3}{x+y}right)cần chứng minh:(vế trái)2/3gefrac{x^3}{y+z}+frac{y^3}{z+x}+frac{z^3}{x+y}Leftrightarrowfrac{x}{y+z}left(frac{x^3+frac{1}{3}}{y+z}-x^2right)+...ge0Leftrightarrowfrac{x^2}{y+z}left(x-yright)left(x-zright)+frac{y^2}{z+x}left(y-xright)left(y-zright)+frac{z^2}{x+y}left(z-xright)left(z-yright)ge0bđt luôn đúng vì là bđt schur mở rộng
Đọc tiếp
ta có:(vế phải)2\(\le3\left(\frac{x^3}{y+z}+\frac{y^3}{z+x}+\frac{z^3}{x+y}\right)\)
cần chứng minh:
(vế trái)2/3\(\ge\frac{x^3}{y+z}+\frac{y^3}{z+x}+\frac{z^3}{x+y}\)
\(\Leftrightarrow\frac{x}{y+z}\left(\frac{x^3+\frac{1}{3}}{y+z}-x^2\right)+...\ge0\)
\(\Leftrightarrow\frac{x^2}{y+z}\left(x-y\right)\left(x-z\right)+\frac{y^2}{z+x}\left(y-x\right)\left(y-z\right)+\frac{z^2}{x+y}\left(z-x\right)\left(z-y\right)\ge0\)
bđt luôn đúng vì là bđt schur mở rộng
Chứng minh BĐT sau: \(\frac{1}{x^2}+\frac{1}{y^2}\ge\frac{8}{\left(x+y\right)^2}\) với x khác y khác 0
Áp dụng bất đẳng thức \(\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\)
\(\frac{1}{x^2}+\frac{1}{y^2}\ge\frac{4}{x^2+y^2}=\frac{8}{2x^2+2y^2}\)
Mặt khác:
\(2x^2+2y^2\ge x^2+y^2+2xy=\left(x+y\right)^2\)
=>\(\frac{1}{x^2}+\frac{1}{y^2}\ge\frac{8}{\left(x+y\right)^2}\)
Ai thấy mình làm đúng thì tích nha.Ai tích mình mình tích lại
Đúng 0
Bình luận (0)
Khánh làm sai rồi
\(2x^2+2y^2\ge x^2+2xy+y^2\Rightarrow\frac{8}{2x^2+2y^2}\le\frac{8}{\left(x+y\right)^2}\)
Đúng 0
Bình luận (0)
\(\Leftrightarrow\frac{x^2+2xy+y^2}{x^2}+\frac{x^2+2xy+y^2}{y^2}\ge8\)
\(\Leftrightarrow\frac{2y}{x}+\frac{2x}{y}+\frac{x^2}{y^2}+\frac{y^2}{x^2}\ge6\)-> là bđt đúng => đpcm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh các bất đẳng thức sau với x, y, z > 0
a) \(x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)
b) \(x^3+y^3\ge\dfrac{\left(x+y\right)^3}{4}\)
c) \(x^4+y^4\ge\dfrac{\left(x+y\right)^4}{8}\)
e) \(x^2+y^2+z^2\ge\dfrac{\left(x+y+z\right)^2}{3}\)
f) \(x^3+y^3+z^3\ge3xyz\)
a) \(x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)
\(\Leftrightarrow2x^2+2y^2\ge\left(x+y\right)^2\Leftrightarrow x^2+y^2\ge2xy\)
\(\Leftrightarrow x^2-2xy+y^2\ge0\Leftrightarrow\left(x-y\right)^2\ge0\left(đúng\right)\)
b) \(x^3+y^3\ge\dfrac{\left(x+y\right)^3}{4}\)
\(\Leftrightarrow4x^3+4y^3\ge\left(x+y\right)^3\Leftrightarrow3x^3+3y^3\ge3x^2y+3xy^2\)
\(\Leftrightarrow3x^2\left(x-y\right)-3y^2\left(x-y\right)\ge0\)
\(\Leftrightarrow3\left(x-y\right)\left(x^2-y^2\right)\ge0\Leftrightarrow3\left(x-y\right)^2\left(x+y\right)\ge0\left(đúng\right)\)
Đúng 1
Bình luận (0)
a: Ta có: \(x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)
\(\Leftrightarrow2x^2+2y^2-x^2-2xy-y^2\ge0\)
\(\Leftrightarrow x^2-2xy+y^2\ge0\)
\(\Leftrightarrow\left(x-y\right)^2\ge0\)(luôn đúng)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Chứng minh BĐT\(4\left(x^3-y^3\right)\ge\left(x-y\right)^3\) với x,y thuộc R
Có thánh nào giúp tui chứng minh BĐT schwarz với
\(\frac{x^2}{a}+\frac{y^2}{b}+\frac{z^2}{c}\ge\frac{\left(x+y+z\right)^2}{\left(a+b+c\right)}\)
Dấu "=" xảy ra khi nào
BĐT tương đương
\(\left(\frac{x^2}{a}+\frac{y^2}{b}+\frac{z^2}{c}\right)\left(a+b+c\right)\ge\left(x+y+z\right)^2\)
sau đó nhân phá ra và đưa về dạng tổng các bình phương
Đúng 0
Bình luận (0)
Chứng minh BĐT sau:
Với a,b>0 thì: \(\frac{x^2}{a}+\frac{y^2}{b}\ge\frac{\left(x+y\right)^2}{a+b}\)
Áp dụng BĐT Cauchy-Schwarz,ta có:\(\left(\frac{x^2}{a}+\frac{y^2}{b}\right)\left(a+b\right)\ge\left(x+y\right)^2\). Chia hai vế cho a, b.Ta được:
\(\frac{x^2}{a}+\frac{y^2}{b}\ge\frac{\left(x+y\right)^2}{a+b}^{\left(đpcm\right)}\)
Dấu "=" xảy ra \(\Leftrightarrow\frac{x}{a}=\frac{y}{b}\)
Đúng 0
Bình luận (0)
Chứng minh BĐT \(\sqrt[3]{\left(x^2+1\right)\left(y^2+1\right)\left(z^2+1\right)}\le\dfrac{\left(x+y+z\right)^2}{3}+1\)
với x,y,z>0 và \(Min\left\{xy,yz,zx\right\}\ge1\)
@Ace Legona: sir tra hộ e câu này đúng hay sai đề vs ,nhẩm mãi không ra điểm rơi
Đúng 0
Bình luận (3)