cho mk hỏi
Cho x,y là hai số thực dương thỏa. mãn x+y>hoặc bằng 5 tìm Pmin của 16/x cộng 1/4y
thanks nhiều lắm ạ
Những câu hỏi liên quan
Cho x,y là 2 số thực dương thỏa mãn x+y=\(\frac{5}{4}\).
Tìm min của A=\(\frac{4}{x}\)+\(\frac{1}{4y}\)
Giúp mình với ạ, cảm ơn nhiều! :))))
A (min) khi
\(\frac{4}{x}=\frac{1}{4y}=>x=16y\)
\(y=\frac{5}{4.17};x=\frac{5.16}{4.17}\)\(x.y=\frac{5.5}{17.17}\)
A(min)=2.\(2\sqrt{\frac{1}{xy}}=2.\frac{17}{5}=\frac{34}{5}\)
Đúng 0
Bình luận (0)
Bạn có thể giải thích rõ hơn cho mình dc ko?? Mình ko hiểu cho lắm!
Đúng 0
Bình luận (0)
Xét các số thực dương x, y thỏa mãn
2018
2
(
x
2
-
y
+
1
)
2
x
+
y...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn 2018 2 ( x 2 - y + 1 ) = 2 x + y ( x + 1 ) 2 . Tìm giá trị nhỏ nhất P m i n của P = 2y - 3x.
A. P m i n = 1 2
B. P m i n = 7 8
C. P m i n = 3 4
D. P m i n = 5 6
Xét các số thực dương x, y thỏa mãn
ln
1
-
2
x
x
+
y
3
x
+
y
-
1
. Tìm giá trị nhỏ nhất
P
m
i
n
của
P
1...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn ln 1 - 2 x x + y = 3 x + y - 1 . Tìm giá trị nhỏ nhất P m i n của P = 1 x + 1 x y
Xét các số thực dương x, y thỏa mãn
ln
(
1
-
2
x
x
+
y
)
3
x
+
y
-
1
.
Tìm giá trị nhỏ nhất
P
m
i
n
của
P
1...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn ln ( 1 - 2 x x + y ) = 3 x + y - 1 . Tìm giá trị nhỏ nhất P m i n của P = 1 x + 1 x y
A . P m i n
B . P m i n
C . P m i n
D . P m i n
Xét các số thực dương x, y thỏa mãn
log
3
1
-
y
x
+
3
x
y
3
x
y
+
x
+
3
y
-
4
. Tìm giá trị nhỏ nhất
P
m
i
n...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn log 3 1 - y x + 3 x y = 3 x y + x + 3 y - 4 . Tìm giá trị nhỏ nhất P m i n của P = x + y
A. P m i n = 4 3 + 4 3
B. P m i n = 4 3 - 4 3
C. P m i n = 4 3 - 4 9
D. P m i n = 4 3 + 4 9
Xét các số thực dương x, y thỏa mãn
log
3
1
-
y
x
+
3
x
y
3
x
y
+
x
+
3
y
-
4
. Tìm giá trị nhỏ nhất
P
m
i
n...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn log 3 1 - y x + 3 x y = 3 x y + x + 3 y - 4 . Tìm giá trị nhỏ nhất P m i n của P = x + y
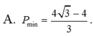
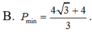
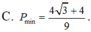
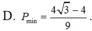
Cho hai số thực dương x,y thỏa mãn x+y lớn hơn hoặc bằng 10. Tìm GTNN:
P=\(2x+y+\frac{30}{x}+\frac{5}{y}\)
\(P=2x+y+\frac{30}{x}+\frac{5}{y}\)
\(=\frac{10x}{5}+\frac{5y}{5}+\frac{30}{x}+\frac{5}{y}\)
\(=\frac{6x}{5}+\frac{4x}{5}+\frac{y}{5}+\frac{4y}{5}+\frac{30}{x}+\frac{5}{y}\)
\(=\left(\frac{6x}{5}+\frac{30}{x}\right)+\left(\frac{4x}{5}+\frac{4y}{5}\right)+\left(\frac{y}{5}+\frac{5}{y}\right)\)
Áp dụng bất đẳng thức cô-si cho hai số không âm
\(\frac{6x}{5}+\frac{30}{x}\ge2\sqrt{\frac{6x}{5}.\frac{30}{x}}=2\sqrt{36}=2.6=12\) (1)
\(\frac{y}{5}+\frac{5}{y}\ge2\sqrt{\frac{y}{5}.\frac{5}{y}}=2\) (2)
Theo đề \(x+y\ge10\) suy ra
\(\frac{4x}{5}+\frac{4y}{5}=\frac{4\left(x+y\right)}{5}\ge\frac{4.10}{5}=8\) (2)
Cộng (1); (2) ; (3) vế theo vế ta được:
\(\frac{6x}{5}+\frac{30}{x}+\frac{y}{5}+\frac{5}{y}+\frac{4x}{5}+\frac{4y}{5}\ge12+2+8=22\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}\frac{6x}{5}=\frac{30}{x}\\\frac{y}{5}=\frac{5}{y}\end{cases}\Rightarrow\hept{\begin{cases}x^2=25\\y^2=25\end{cases}}}\)
Vì x;y dương nên (x;y) = (5;5)
Đúng 0
Bình luận (0)
\(P=2x+y+\frac{30}{x}+\frac{5}{y}\)
\(\Leftrightarrow P=0,8\left(x+y\right)+\left(1,2x+\frac{30}{x}\right)+\left(0,2y+\frac{5}{y}\right)\)
Áp dụng BĐT AM-GM ta có:
\(P\ge0,8\left(x+y\right)+2.\sqrt{1,2x.\frac{30}{x}}+2.\sqrt{0,2y.\frac{5}{y}}=8+12+2=22\)
Dấu " = " xảy ra <=> x=y=5
Vậy \(P_{min}=22\Leftrightarrow x=y=5\)
Đúng 1
Bình luận (0)
Xét các số thực dương x;y thỏa mãn
log
3
1
-
y
x
+
3
x
y
3
x
y
+
x
+
3
y
-
4
. Tìm giá trị nhỏ nhất
P...
Đọc tiếp
Xét các số thực dương x;y thỏa mãn log 3 1 - y x + 3 x y = 3 x y + x + 3 y - 4 . Tìm giá trị nhỏ nhất P m i n của biểu thức P=x+y..
A. P m i n = 4 3 - 4 3
B. P m i n = 4 3 + 4 3
C. P m i n = 4 3 + 4 9
D. P m i n = 4 3 - 4 9
ĐK:
Ta có
log 3 1 - y x + 3 x y = 3 x y + x + 3 y - 4
Xét hàm số f ( x ) = log 3 t + 3 t t > 0
có f ' ( t ) = 1 t ln 3 + 3 > 0 ; ∀ t > 0 nên hàm số đồng biến trên 0 ; + ∞
Kết hợp (*) suy ra
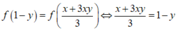
Xét P = x + y ⇒ x = P - y thay vào (**) ta được
Ta tìm giá trị nhỏ nhất của g ( y ) = 3 y 2 - 2 y + 3 3 y + 1 trên (0;1)
Ta có
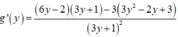
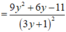
Giải phương trình
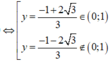
Lại có g ' ( y ) < 0 ∀ y ∈ 0 ; - 1 + 2 3 3
và g ' ( y ) > 0 ∀ y ∈ - 1 + 2 3 3 ; 1
Hay g'(y) đổi dấu từ âm sang dương tại y = - 1 + 2 3 3 nên
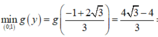
⇒ P m i n = 4 3 - 4 3
Chọn đáp án A.
Đúng 0
Bình luận (0)
Xét các số thực dương x;y thỏa mãn
log
3
1
-
y
x
+
3
x
y
3
x
y
+
x
+
3
y
-
4
. Tìm giá trị nhỏ nhất
P...
Đọc tiếp
Xét các số thực dương x;y thỏa mãn log 3 1 - y x + 3 x y = 3 x y + x + 3 y - 4 . Tìm giá trị nhỏ nhất P m i n của biểu thức P = x + y.
A. P m i n = 4 3 - 4 3
B. P m i n = 4 3 + 4 3
C. P m i n = 4 3 + 4 9
D. P m i n = 4 3 - 4 9
