a)

\(\left[\left(x-81\right)^3:5^3\right]-2^3=0\\ =>\left(x-81\right)^3:5^3=2^3\\ =>\left(x-81\right)^3=2^3.5^3=10^3\\ =>x-81=10\\ =>x=91\)

b) 

\(3^{n+1}.3^{n+3}=18^{10}:6^{10}\\ =>3^{n+1+n+3}=3^{10}\\ =>2n+4=10\\ =>2n=6=>n=3\)

a) \(\left[\left(x+81\right)^3:5^3\right]-2^3=0\)

\(\Rightarrow\left(\dfrac{x+81}{5}\right)^3=2^3\)

\(\Rightarrow\dfrac{x-81}{5}=2\)

\(\Rightarrow x-81=10\)

\(\Rightarrow x=91\)

b) \(3^{n+1}\cdot3^{n+3}=18^{10}:6^{10}\)

\(\Rightarrow3^{2n+4}=3^{10}\)

\(\Rightarrow2n+4=10\)

\(\Rightarrow2n=6\)

\(\Rightarrow n=3\)

\(\Leftrightarrow n^3+n^2-n^2-n-2n-2+6⋮n+1\)

\(\Leftrightarrow n+1\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)

hay \(n\in\left\{0;-2;1;-3;2;-4;5;-7\right\}\)

Ta có :

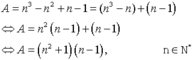
Nếu n = 1 suy ra A = 0

Nếu n = 2 suy ra A = 5 là số nguyên tố

Nếu n>2 thì A là tích của hai thừa số mà mỗi thừa số đều lớn hơn hai . Vậy A là hợp số

Vậy để A = n³ – n² + n – 1 là số nguyên tố thì n = 2.

`P=n^3-n^2+n-1`

`=n^2(n-1)+(n-1)`

`=(n-1)(n^2+1)`

Vì n là stn thì p là snt khi

`n-1=1=>n=2`

Vậy n=2

\(2,\\ n=0\Leftrightarrow A=1\left(loại\right)\\ n=1\Leftrightarrow A=3\left(nhận\right)\\ n>1\Leftrightarrow A=n^{2012}-n^2+n^{2002}-n+n^2+n+1\\ \Leftrightarrow A=n^2\left[\left(n^3\right)^{670}-1\right]+n\left[\left(n^3\right)^{667}-1\right]+\left(n^2+n+1\right)\)

Ta có \(\left(n^3\right)^{670}-1⋮\left(n^3-1\right)=\left(n-1\right)\left(n^2+n+1\right)⋮\left(n^2+n+1\right)\)

Tương tự \(\left(n^3\right)^{667}⋮\left(n^2+n+1\right)\)

\(\Leftrightarrow A⋮\left(n^2+n+1\right);A>1\)

Vậy A là hợp số với \(n>1\)

Vậy \(n=1\)

\(3,\)

Đặt \(A=n^4+n^3+1\)

\(n=1\Leftrightarrow A=3\left(loại\right)\\ n\ge2\Leftrightarrow\left(2n^2+n-1\right)^2\le4A\le\left(2n^2+n\right)^2\\ \Leftrightarrow4A=\left(2n^2+n\right)^2\\ \Leftrightarrow4n^2+4n^3+4=4n^2+4n^3+n^2\\ \Leftrightarrow n^2=4\Leftrightarrow n=2\)

Vậy \(n=2\)

a: \(n^3-2⋮n-2\)

=>\(n^3-8+6⋮n-2\)

=>\(6⋮n-2\)

=>\(n-2\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)

=>\(n\in\left\{3;1;4;0;5;-1;8;-4\right\}\)

b: \(n^3-3n^2-3n-1⋮n^2+n+1\)

=>\(n^3+n^2+n-4n^2-4n-4+3⋮n^2+n+1\)

=>\(3⋮n^2+n+1\)

=>\(n^2+n+1\in\left\{1;-1;3;-3\right\}\)

mà \(n^2+n+1=\left(n+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}\forall n\)

nên \(n^2+n+1\in\left\{1;3\right\}\)

=>\(\left[{}\begin{matrix}n^2+n+1=1\\n^2+n+1=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}n^2+n=0\\n^2+n-2=0\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}n\left(n+1\right)=0\\\left(n+2\right)\left(n-1\right)=0\end{matrix}\right.\Leftrightarrow n\in\left\{0;-1;-2;1\right\}\)

\(P=\dfrac{n^3+3n^2+2n}{6}+\dfrac{2n+1}{1-2n}\)

Vì n^3+3n^2+2n=n(n+1)(n+2) là tích của 3 số liên tiếp

nên n^3+3n^2+2n chia hết cho 3!=6

=>Để P nguyên thì 2n+1/1-2n nguyên

=>2n+1 chia hết cho 1-2n

=>2n+1 chia hết cho 2n-1

=>2n-1+2 chia hết cho 2n-1

=>\(2n-1\in\left\{1;-1;2;-2\right\}\)

=>\(n\in\left\{1;0;\dfrac{3}{2};-\dfrac{1}{2}\right\}\)

Đáp án B.

Ta có u n = u n − 1 + n − 1 3 ⇔ u n − u n − 1 = n − 1 3 ⇒ u n − 1 − u n − 2 = n − 2 3 .

Tương tự, ta được u 2 − u 1 = 1 3 .  Cộng trừ 2 vế suy ra u n − u 1 = 1 3 + 2 3 + ... + n − 1 3  

⇔ u n − 1 = n n − 1 2 2 ⇒ u n − 1 = n n − 1 2 ≥ 2039190 ⇔ n ≥ 2020.