Cho 2 điểm M(−2;3;1),N(5;6;−2) có hình chiếu vuông góc lên trục Ox lần lượt là A,B khi đó tỷ số:

Những câu hỏi liên quan
Vẽ hai đường thẳng a, b và hai điểm M, N sao cho M ∈ a, M ∈ b, N ∈ b. Vẽ điểm P sao cho 2 điểm N và P nằm khác phía so với điểm M. Vẽ 2 điểm K và F thuộc đường thẳng a sao cho 2 điểm K và F cùng phía so với điểm M.
1}Cho 2 tia chung gốc O là Ox và Oy .Trên đường thẳng x lấy điểm O . Trên tia Ox lấy điểm M sao cho OM bằng 2 cm . Trên tia Oy lấy điểm N sao cho ON 2 cm và OPa2cma) Chứng tỏ rằng O là trung điểm của MNb)Tìm giá trị của a sao cho N là trung điểm của OP2}Cho ddoanj thẳng AB 2^10 cm . Gọi M-1 là trung điểm của đoạn thẳng AB ; M-2 là trung điểm của doạn thẳng M-1B ; M-3 là trung điểm của đoạn thẳng M-2B ; ... ;M-10 là trung điểm của đoạn thẳng M-9B.Tính độ dài đoạn thẳng M-1;M-9;M-10 .
Đọc tiếp
1}Cho 2 tia chung gốc O là Ox và Oy .Trên đường thẳng x lấy điểm O . Trên tia Ox lấy điểm M sao cho OM bằng 2 cm . Trên tia Oy lấy điểm N sao cho ON = 2 cm và OP=a>2cm
a) Chứng tỏ rằng O là trung điểm của MN
b)Tìm giá trị của a sao cho N là trung điểm của OP
2}Cho ddoanj thẳng AB = 2^10 cm . Gọi M-1 là trung điểm của đoạn thẳng AB ; M-2 là trung điểm của doạn thẳng M-1B ; M-3 là trung điểm của đoạn thẳng M-2B ; ... ;M-10 là trung điểm của đoạn thẳng M-9B.Tính độ dài đoạn thẳng M-1;M-9;M-10 .
1. Cho AB2 ,I là trung điểm AB. Tìm tập hợp các điểm M sao cho MA^2-MB^282. Trg mp vs hệ tọa độ Oxy , cho 2 điểm A(1;-2) và B (2;3). Gọi M (a;0) là điểm sao cho tứ giác OABM là hình thang . Tìm a3. Tìm tất cả các gtri của m để pt sqrt{2x^2-x-2m}m-2 có nghiệm 4. Tìm tất cả giá trị của m để pt x^2-2x-3-m0 có nghiệm xin[0;4]Help me
Đọc tiếp
1. Cho AB=2 ,I là trung điểm AB. Tìm tập hợp các điểm M sao cho \(MA^2-MB^2=8\)
2. Trg mp vs hệ tọa độ Oxy , cho 2 điểm A(1;-2) và B (2;3). Gọi M (a;0) là điểm sao cho tứ giác OABM là hình thang . Tìm a
3. Tìm tất cả các gtri của m để pt \(\sqrt{2x^2-x-2m}=m-2\) có nghiệm
4. Tìm tất cả giá trị của m để pt \(x^2-2x-3-m=0\) có nghiệm \(x\in[0;4]\)
Help me
Cho \(\left(P\right):y=x^2\) và (d):\(y=2.\left(m-1\right)x+m^2+2m\). Tìm 2 điểm thuộc (P) sao cho 2 điểm đó đối xứng với nhau qua M(-1;5)
Gọi \(A\left(x_1;x_1^2\right)\) và \(B\left(x_2;x_2^2\right)\) là 2 điểm thuộc (P) và đối xứng qua M
Do A; B đối xứng qua M
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=2.\left(-1\right)\\x_1^2+x_2^2=2.5\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_2=-2-x_1\\x_1^2+x_2^2=10\end{matrix}\right.\)
\(\Rightarrow x_1^2+\left(-2-x_1\right)^2=10\)
\(\Rightarrow2x_1^2+4x_1-6=0\Rightarrow\left[{}\begin{matrix}x_1=1\\x_1=-3\end{matrix}\right.\)
Vậy 2 điểm đó là \(\left(1;1\right)\) và \(\left(-3;9\right)\)
Đúng 1
Bình luận (0)
Cho điểm O nằm giữa 2 điểm A và B. Điểm M nằm giữa 2 điểm O và A, điểm N nằm giữa 2 điểm O và B.
A) CMR: Điểm O nằm giữa 2 điểm M và N.
B) CMR: Điểm M nằm giữa 2 điểm A và N
Cho 4 điểm A,B,C,M trong đó điểm B nằm giữa 2 điểm A,C; điểm M nằm giữa 2 điểm A,B; Hỏi trong 3 điểm B,C,M điểm nào nằm giữa 2 điểm còn lại?
Cho hai điểm A(-3; 2), B(4; 3). Biết có 2 điểm M trên trục Ox sao cho tam giác MAB vuông tại M. Tính tổng hoành độ 2 điểm đó.
A. -1
B. 0
C. 1
D. 2
Chọn C.
Điểm M ∈ Ox ⇒ M(x; 0).
Khi đó ![]()
ΔMAB vuông tại M nên ![]()
Hay (–3 – x)(4 – x) + 2.3 = 0
⇔ –12 + 3x – 4x + x2 + 6 = 0
⇔ x2 – x – 6 = 0 ⇔ 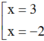 .
.
Vậy: M1(3; 0), M2(-2; 0) và tổng hoành độ của chúng là : 3 + (-2) = 1.
Đúng 0
Bình luận (0)
1. cho hàm số y(m - 1)x2+2mx -3m + 1(1+�)�2−2(�−1)2 +�−3 (Pm) (��). tìm điểm cố định2. cho hàm sốym^2x^2+2left(m-1right)+m^2-1left(P_mright) . tìm điểm cố định
Đọc tiếp
1. cho hàm số . tìm điểm cố định
2. cho hàm số
\(y=m^2x^2+2\left(m-1\right)+m^2-1\left(P_m\right)\) . tìm điểm cố định
Bài 1:
\(y=\left(m-1\right)x^2+2mx-3m+1\)
\(=mx^2-x^2+2mx-3m+1\)
\(=m\left(x^2+2x-3\right)-x^2+1\)
Tọa độ điểm cố định mà (Pm) luôn đi qua là:
\(\left\{{}\begin{matrix}x^2+2x-3=0\\y=-x^2+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x+3\right)\left(x-1\right)=0\\y=-x^2+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x+3=0\\x-1=0\end{matrix}\right.\\y=-x^2+1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x+3=0\\y=-x^2+1\end{matrix}\right.\\\left\{{}\begin{matrix}x-1=0\\y=-x^2+1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=-3\\y=-\left(-3\right)^2+1=-9+1=-8\end{matrix}\right.\\\left\{{}\begin{matrix}x=1\\y=-1^2+1=0\end{matrix}\right.\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho điểm O nằm giữa 2 điểm A và B :
Điểm M nằm giữa 2 điểm A và O, Điểm N nằm giữa 2 điểm O và B.
Chứng minh rằng :
a) M nằm giữa 2 điểm A và B
b) O nằm giữa 2 điểm M và N
c) N nằm giữa 2 điểm M và B
Cho góc bẹt xOy, trên tia Ox lấy điểm A sao cho OA = 2cm, trên tia Oy lấy 2 điểm M và B sao cho OM = 1cm; OB = 4cm. a) Chứng tỏ : Điểm M nằm giữa 2 điểm O và B và điểm M là trung điểm của đoạn thẳng AB. b) Từ O kẻ 2 tia Ot và Oz sao cho tOy = 130 độ ; zOy= 30 độ.Tính tOy Các bn chỉ cần làm phần b thôi (nhé vẽ hình)
a: Trên tia Oy, ta có: OM<OB
nên điểm M nằm giữa hai điểm O và B
=>BM+MO=BO
hay BM=3(cm)
Ta có: OM và OA là hai tia đối nhau
nên điểm O nằm giữa hai điểm A và M
=>OA+OM=AM
hay AM=3(cm)
Ta có: điểm M nằm giữa hai điểm A và B
mà MA=MB
nên M là trung điểm của AB
b: \(\widehat{tOy}=130^0\)
Đúng 0
Bình luận (0)
a: Trên tia Oy, ta có: OM<OB
nên điểm M nằm giữa hai điểm O và B
=>BM+MO=BO
hay BM=3(cm)
Ta có: OM và OA là hai tia đối nhau
nên điểm O nằm giữa hai điểm A và M
=>OA+OM=AM
hay AM=3(cm)
Ta có: điểm M nằm giữa hai điểm A và B
mà MA=MB
nên M là trung điểm của AB
b: \(\widehat{tOy}\) = \(130^{o}\)
Đúng 0
Bình luận (0)
















