Giải phương trình lượng giác bậc nhất đối với hàm số lượng giác
3cos x - 3 =0
Giải phương trình lượng giác đối với hàm số lượng giác
3cos x - 3=0
Giải phương trình lượng giác bậc nhất đối với sinx và cosx:
\(cos3x-sinx=\sqrt{3}\left(cosx-sin3x\right)\)
\(\Leftrightarrow cos3x+\sqrt{3}sin3x=\sqrt{3}cosx+sinx\)
\(\Leftrightarrow\dfrac{1}{2}cos3x+\dfrac{\sqrt{3}}{2}sin3x=\dfrac{\sqrt{3}}{2}cosx+\dfrac{1}{2}sinx\)
\(\Leftrightarrow cos\left(3x-\dfrac{\pi}{3}\right)=cos\left(x-\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\dfrac{\pi}{3}=x-\dfrac{\pi}{6}+k2\pi\\3x-\dfrac{\pi}{3}=\dfrac{\pi}{6}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{12}+k\pi\\x=\dfrac{\pi}{8}+\dfrac{k\pi}{2}\end{matrix}\right.\)
Câu 1: Phương trình lượng giác: sin^2 x - 3cos x - 4 = 0 có nghiệm là: A. x=- pi 2 +k 2 pi B. x=- pi+k2 pi C. x = pi/6 + k*pi D.Vô nghiệm
1.D
sin2x - 3cosx - 4 = 0
1-cos2x - 3cosx - 4 = 0
cos2x + 3 cosx + 3 = 0
Vô nghiệm
Giải phương trình lượng giác sau: ( dạng pt bậc nhất theo sin và cos )
3cosx + 4sinx + 6/3cosx+ 4sinx+1 =2
Đề như vậy hả bạn: \(\frac{3cosx+4sinx+6}{3cosx+4sinx+1}=2\)
Cho hàm số f(x) = sin2x + 2cosx. Số điểm biểu diễn nghiệm của phương trình f’(x)=0 trên đường tròn lượng giác là:
A. 2
B. 3
C. 4
D. Vô số
Cho hàm số f(x)=sin2x+2cosx. Số điểm biểu diễn nghiệm của phương trình f ' ( x ) = 0 trên đường tròn lượng giác là:
A. 2
B. 3
C. 4
D. Vô số
Giải phương trình 2sinx – 3 = 0 là phương trình bậc nhất đối với sinx.
2sinx – 3 = 0 ⇔ sin x = 3/2 , vô nghiệm vì |sinx| ≤ 1
Giải phương trình lượng giác 2 co s x 2 + 3 = 0 có nghiệm là
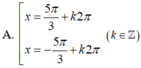
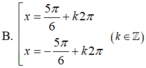
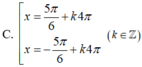
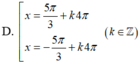
\(cos2x+2cosx-sin^2\dfrac{x}{2}=0\)
Giải phương trình lượng giác
\(\Leftrightarrow2cos^2x-1+2cosx-\left(\dfrac{1}{2}-\dfrac{1}{2}cosx\right)=0\)
\(\Leftrightarrow2cos^2x+\dfrac{5}{2}cosx-\dfrac{3}{2}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\dfrac{-5+\sqrt{73}}{8}\\cosx=\dfrac{-5-\sqrt{73}}{8}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x=\pm arccos\left(\dfrac{-5+\sqrt{73}}{8}\right)+k2\pi\)