Cho hình chóp S.ABCD, SA ⊥(ABCD). ABCD là hình vuông:
a)CM BC ⊥(SAB)
b)CM (SBD) ⊥ (SAC)
Những câu hỏi liên quan
cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với đáy SA=a căn 3 a)cm SAC vuông góc với SBD b)gọi AH là đg cao của tam giác SAB . cmr AK vuông góc với (SBC) c) tính góc giữa đg thẳng SC và mặt đáy ABC d) tính khoảng cách từ a đến mp (SCD)
a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>BC vuông góc AK
mà AK vuông góc SB
nên AK vuông góc (SBC)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật ACa căn 3, BC 2a, SA vuông góc (ABCD), SA3a. Gọi O là giao điểm của AC và BD.a) Cmr: CD vuông góc mp (SAD)b) Cmr: (SAC) vuông góc mp (SBD)c) Tính góc giữa SC v à mp (ABCD)d) Tính góc giữa mp ( SAB) và mp (SBC).e) Tính khoảng cách từ A đến mp ( SBD)
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AC=a căn 3, BC = 2a, SA vuông góc (ABCD), SA=3a. Gọi O là giao điểm của AC và BD.
a) Cmr: CD vuông góc mp (SAD)
b) Cmr: (SAC) vuông góc mp (SBD)
c) Tính góc giữa SC v à mp (ABCD)
d) Tính góc giữa mp ( SAB) và mp (SBC).
e) Tính khoảng cách từ A đến mp ( SBD)
a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
c: (SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=căn 3
=>góc SCA=60 độ
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B;
A
B
B
C
1
,
A
D
2.
Các mặt chéo
S
A
C
và
S
B
D
cùng vuông góc với mặt đáy
A
B
C
D...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B; A B = B C = 1 , A D = 2. Các mặt chéo S A C và S B D cùng vuông góc với mặt đáy A B C D . Biết góc giữa hai mặt phẳng S A B và A B C D bằng 60 0 (tham khảo hình vẽ bên). Khoảng cách từ điểm D đến mặt phẳng S A B là
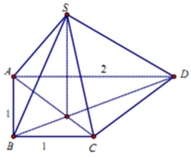
A. 2 3 3
B. 3
C. 2 3
D. 3 3
Hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB 3cm, BC 4 cm, SC 5 cm. Tam giác SAC nhọn và nằm trong mặt phẳng vuông góc với (ABCD). Các mặt (SAB) và (SAC) tạo với nhau một góc
α
sao cho
α
3
29
. Tính thể tích khối chóp S.ABCD
A
.
16
c
m
2
B
.
15
29...
Đọc tiếp
Hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 3cm, BC = 4 cm, SC = 5 cm. Tam giác SAC nhọn và nằm trong mặt phẳng vuông góc với (ABCD). Các mặt (SAB) và (SAC) tạo với nhau một góc α sao cho α = 3 29 . Tính thể tích khối chóp S.ABCD
A . 16 c m 2
B . 15 29 c m 2
C . 20 c m 2
D . 18 5 c m 2
Đáp án A
Gọi chiều cao của hình chóp là h => h < SC = 5 cm
Đúng 0
Bình luận (0)
cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, SA vuông góc (ABCD), SA=a căn 2
1.chứng minh : các mặt bên của hình chóp là tam giác vuông
2. (SAC) vuông góc (SBD)
3.Tính (SC,(SAB))
4.tan ((SBD),(ABCD))
5.d(A,(SBC)),d(A,(SCD))
6.d(SC,BD)
7.Hãy chỉ ra điểm I cách đều S,A,B,C,D. tính SI
1.SA \(\perp\)AB , SA\(\perp\)AD =>SAB vuông tại A, SAD vuông tại A
\(\begin{cases}AB\perp BC\left(hvABCD\right)\\SA\perp BC\left(SA\perp mpABCD\right)\end{cases}\) =>(SAB)\(\perp\)BC =>SB\(\perp\)BC =>SBC vuông tại B
\(\begin{cases}AD\perp CD\\SA\perp CD\end{cases}\) =>(SAD)\(\perp\)CD =>SD\(\perp\)CD =>SCD vuông tại D
Đúng 0
Bình luận (1)
SGK Chân trời sáng tạo
20 tháng 8 2023 lúc 21:49
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, \(SA\) vuông góc với mặt đáy. Đường thẳng \(C{\rm{D}}\) vuông góc với mặt phẳng nào sau đây?
A. \(\left( {SAD} \right)\).
B. \(\left( {SAC} \right)\).
C. \(\left( {SAB} \right)\).
D. \(\left( {SBD} \right)\).
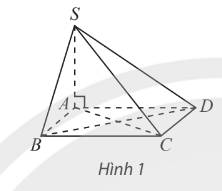
Ta có:\(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD.\)
\(ABCD\) là hình vuông \(\Rightarrow CD\perp AD.\)
\(\Rightarrow CD\perp\left(SAD\right).\)
\(\Rightarrow A\)
Đúng 1
Bình luận (0)
cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh AB=2a, SI vuông góc ( ABCD) vs I là trung điểm canh AB và SI=a√5. Gọi M là trung điểm của BC. a) CM BC vuông góc (SAB) và IM vuông góc (SBD) b) tính góc giữa SC và (ABCD)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và S A = a 15 Gọi M, N lần lượt là trung điểm của BC và CD: Chứng minh (SAC) ⊥ (SBD).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SASBSCSDa√2; O là tâm của hình vuông ABCD.a) C/m (SAC) và (SBD) cùng vuông góc với (ABCD). b) C/m (SAC) ⊥(SBD)c) Tính khoảg cách từ S đến (ABCD)d) Tính góc giữa đường SB và (ABCD).e) Gọi M là trung điểm của CD, hạ OH⊥SM, chứng minh H là trực tâm tam giác SCDf) Tính góc giưa hai mặt phẳng (SCD) và (ABCD)g) Tính khoảng cách giữa SM và BC; SM và AB.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA=SB=SC=SD=a√2; O là tâm của hình vuông ABCD.
a) C/m (SAC) và (SBD) cùng vuông góc với (ABCD).
b) C/m (SAC) ⊥(SBD)
c) Tính khoảg cách từ S đến (ABCD)
d) Tính góc giữa đường SB và (ABCD).
e) Gọi M là trung điểm của CD, hạ OH⊥SM, chứng minh H là trực tâm tam giác SCD
f) Tính góc giưa hai mặt phẳng (SCD) và (ABCD)
g) Tính khoảng cách giữa SM và BC; SM và AB.
a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, S A = a 2 . Chứng minh rằng: (SAC) ⊥ (SBD).
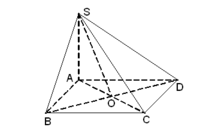
● BD ⊥ AC, BD ⊥ SA
⇒ BD ⊥ (SAC) ⇒ (SBD) ⊥ (SAC).
Đúng 0
Bình luận (0)