Cho tam giác ABC~tam giác DEF có AB/DE=2/3 và Diện tích DEF=45cm².Khi đó ta có
a)Sabc=20cm²
b)Sabc=30cm²
c)Sabc=35cm²
d)Sabc=40cm²
Những câu hỏi liên quan
tam giác abc có góc a<90 trên cạnh ab lấy d trên cạnh ac lấy e gọi diện tích tam abc là Sabc diện tích tam ade là Sade a ,chứng minh Sade/Sabc =ad.ae/ab.ac b, cho de //bc xác định vị trí của d để diện tích tam giác bde lớn nhất
dễ thấy Sabc =\(\frac{1}{2}\) AB.AC.sinA; Sade= \(\frac{1}{2}\)AD.AE.sinA
=> Sabc/Sade=ad.ae/ab.ac
de//bc thì \(\frac{AD}{AB}=\frac{DE}{BC}=>\frac{BD}{AB}=\frac{BC-DE}{BC}=>BD=\frac{AB\left(BC-DE\right)}{BC}\)
SBDE = \(\frac{1}{2}BD.DEsin\widehat{BDE}=\frac{1}{2}\frac{AB\left(BC-DE\right)}{BC}.DE.cos\widehat{ABC}=\)\(\frac{AB.cos\widehat{ABC}}{2BC}\left(BC.DE-DE^2\right)\)
BC.DE - DE2 = \(\frac{BC^2}{4}-\)(\(\frac{BC}{2}-DE\))2 \(\le\frac{BC^2}{4}\)
vậy SBDE đạt GTLN khi DE= \(\frac{BC}{2}\)hay \(\frac{DE}{BC}=\frac{1}{2}=\frac{AD}{AB}\) hay D là trung điểm AB
6 tháng 12 2021 lúc 19:31
1 đường thẳng song song với BC của tam giác ABC cát AB, AC lần lượt tại D và E. CMR: Mọi điểm F trên BC ta luôn có SDEF ≤ \(\dfrac{1}{4}\) SABC. Dường thẳng DE ở vị trí nào thì tam giác DEF có S lớn nhất.
cho tam giác ABC vuông tại A có AB=30cm, AC=40cm. a) Tính Sabc. b) Gọi M,N trung điểm AB, AC. Tính Smncb
Giúp mình vs mn ơi.!
Xem chi tiết
Lời giải:
a) Do tam giác $ABC$ vuông tại $A$ nên:
$S_{ABC}=\frac{AB.AC}{2}=\frac{30.40}{2}=600$ (cm2)
b) Do $M,N$ lần lượt là trung điểm của $AB, AC$ nên:
$AM=\frac{1}{2}AB=\frac{1}{2}.30=15$ (cm)
$AN=\frac{1}{2}AC=\frac{1}{2}.40=20$ (cm)
$S_{AMN}=\frac{AM.AN}{2}=\frac{15.20}{2}=150$ (cm2)
$S_{MNCB}=S_{ABC}-S_{AMN}=600-150=450$ (cm2)
Đúng 1
Bình luận (0)
Cho tam giác vuông cân ABC có cạnh huyền AB = 2a. Trên đường thẳng d đi qua A và vuông góc với mặt phẳng (ABC), lấy một điểm S khác A, ta được tứ diện SABC. Xác định tâm mặt cầu ngoại tiếp tứ diện SABC.
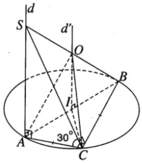
Gọi I là trung điểm của cạnh AB. Vì tam giác ABC vuông cân tại C nên ta có IA = IB = IC. Vậy I là tâm đường tròn ngoại tiếp tam giác ABC. Do đó, tâm mặt cầu ngoại tiếp tứ diện SABC phải nằm trên đường thẳng d’ vuông góc với mặt phẳng (ABC) tại I. Ta suy ra d’ // d. Do đó d’ cắt SB tại trung điểm O của đoạn SB. Ta có OB = OS = OA = OC và như vậy O là tâm đường tròn ngoại tiếp tứ diện SABC.
Đúng 0
Bình luận (0)
1. Cho tam giác ABC cân tại A, đg cao AH, O là tđ của AH, BO và CO cắt AB,AC tại D,E. Tính Sadoe biết Sabc=108cm2
2,Cho tam giác ABC cân tại A, có 2 đg cao AH=10,BD=12. Tính Sabc
3, cho tam giác ABC có AB=20, AC=34,BC=42. Tính Sabc
Bạn nào làm gấp giúp mk vs ạ, thanks trước
Hình chóp SABC có chiều cao ha, diện tích tam giác ABC là
3
a
2
. Tính thể tích hình chóp SABC A.
a
3
3
B.
a
3
C.
3
2
a
3
D.
3
a
3
Đọc tiếp
Hình chóp SABC có chiều cao h=a, diện tích tam giác ABC là 3 a 2 . Tính thể tích hình chóp SABC
A. a 3 3
B. a 3
C. 3 2 a 3
D. 3 a 3
Hình chóp tam giác đều SABC có AB a, (SC;(ABC)) 60
°
. Tính thể tích V của SABC A. V
a
3
4
B. V
a
3
3
12
C. V
a
3
3
4
D. V...
Đọc tiếp
Hình chóp tam giác đều SABC có AB = a, (SC;(ABC)) = 60 ° . Tính thể tích V của SABC
A. V = a 3 4
B. V = a 3 3 12
C. V = a 3 3 4
D. V = a 3 12
1 .Cho tam giác Abc vuông ở A . có chu vi = 24cm . có cạnh Ab = 3/4 Ac ; Bc =10cm . tính Sabc
2. Cho ∆ ABC có cạnh BC = 32cm . nếu kéo dài cạnh AB thêm 4cm thì Sabc sẽ tăng 52cm2 . tính SAbc
3. ∆ abc có ab = 50 cm . nếu kéo dài bc thêm 1 đoạn cd = 30cm thì ∆ abc là ∆ cân vs ab = ad và ∆ acd có chiều cao hạ từ c=18cm . tính S abc biết chu vi ABD là 180cm
Giải hộ ☺
Cho tứ diện SABC có ABC là tam giác vuông cân tại A, đường cao SA. Biết đường cao AH của tam giác ABC bằng a, góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng
60
0
.Tính theo a thể tích khối tứ diện SABC
A
.
a
3
6
3
B
.
a...
Đọc tiếp
Cho tứ diện SABC có ABC là tam giác vuông cân tại A, đường cao SA. Biết đường cao AH của tam giác ABC bằng a, góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng 60 0 .Tính theo a thể tích khối tứ diện SABC
A . a 3 6 3
B . a 3 3 3
C . 2 a 3 6 3
D . a 3 2 3
