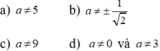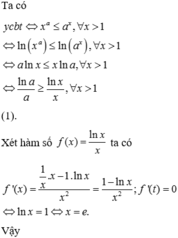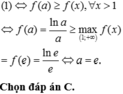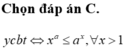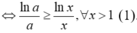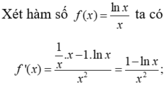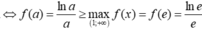giải bất phương trình : (a+1)x +ax-1/a >1/a

Những câu hỏi liên quan
Giải và biện luận các bất phương trình
a) \(\left(m-2\right)\ge\left(2m-1\right)x-3\)
b) \(\frac{ax+1}{a-1}>\frac{ax-1}{a+1}\) với a>1
a. \(m-2\ge\left(2m-1\right)x-3\Leftrightarrow m+1\ge\left(2m-1\right)x\)
Với \(2m-1=0\Rightarrow m=\frac{1}{2},bpt\Leftrightarrow\frac{3}{2}\ge0\) đúng với mọi x.
Với \(2m-1>0\Rightarrow m>\frac{1}{2},bpt\Leftrightarrow x\le\frac{m+1}{2m-1}\)
Với \(2m-1< 0\Rightarrow m< \frac{1}{2},bpt\Leftrightarrow x\ge\frac{m+1}{2m-1}\)
Với \(m>\frac{1}{2},\) S = ( \(-\infty;\frac{m+1}{2m-1}\)]
Vậy với \(m=\frac{1}{2}\Rightarrow S=R.\)
Với \(m< \frac{1}{2},\)S = [ \(\frac{m+1}{2m-1};+\infty\))
b. \(bpt\Leftrightarrow\frac{\left(ax+1\right)\left(a+1\right)-\left(ax-1\right)\left(a-1\right)}{a^2-1}>0\)
\(\Leftrightarrow\frac{2ax+2a}{a^2-1}>0\)
Với a > 1 thì \(a^2-1>0\Rightarrow ax+a>0\Rightarrow x+1>0\Rightarrow x>-1\forall a>1\)
Vậy với a > 1 thì bpt luôn có tập nghiệm \(S=\left(-1;+\infty\right)\)
Đúng 0
Bình luận (0)
Tìm a để các bất phương trình sau là bất phương trình bậc nhất ẩn x:a)
a
−
5
x
6
;
b)
(
2
a
2
−
1
)
x
+
7
≥
0
;
c)
−
a
+
9...
Đọc tiếp
Tìm a để các bất phương trình sau là bất phương trình bậc nhất ẩn x:
a) a − 5 x < 6 ; b) ( 2 a 2 − 1 ) x + 7 ≥ 0 ;
c) − a + 9 3 x − 3 a 5 < 0 ; d) ax − 5 3 − a ≤ 0 .
Giải bất phương trình với a,b là các hằng số( a khác 0).
\(\frac{ax-b}{a}+(a+b+1)x>\frac{2b}{a}\)
\(\frac{ax-b}{a}+(a+b+1)x>\frac{2b}{a}\)
<=> \(x-\frac{b}{a}+\left(a+b+1\right)x>\frac{2b}{a}\)
<=> \(\left(a+b+2\right)x>\frac{3b}{a}\)
Giờ biện luận theo a và b thôi
Bài I: 1) Giải các phương trình a/8 + 4x = 3x – 1
2) Giải các bất phương trình a) 10 - 5(x + 3) > 3(x - 1)
1) Ta có: \(4x+8=3x-1\)
\(\Leftrightarrow4x-3x=-1-8\)
\(\Leftrightarrow x=-9\)
2) Ta có: \(10-5\left(x+3\right)>3\left(x-1\right)\)
\(\Leftrightarrow10-5x-15-3x+3>0\)
\(\Leftrightarrow-8x>2\)
hay \(x< \dfrac{-1}{4}\)
Đúng 1
Bình luận (0)
Cho a 1. Biết khi
a
a
0
thì bất phương trình
x
a
≤
a
x
đúng với mọi
x
∈
1
;
+
∞
. Mệnh đề nào dưới đây đúng? A.
1
a
0
2
B....
Đọc tiếp
Cho a > 1. Biết khi a = a 0 thì bất phương trình x a ≤ a x đúng với mọi x ∈ 1 ; + ∞ . Mệnh đề nào dưới đây đúng?
A. 1 < a 0 < 2
B. e < a 0 < e 2
C. 2 < a 0 < 3
D. e 2 < a 0 < e 3
Cho a 1. Biết khi
a
a
o
thì bất phương trình
x
a
≤
a
x
đúng với mọi
x
∈
1
;
+
∞
Mệnh đề nào dưới đây đúng? A. B. C. D.
Đọc tiếp
Cho a > 1. Biết khi a = a o thì bất phương trình x a ≤ a x đúng với mọi x ∈ 1 ; + ∞ Mệnh đề nào dưới đây đúng?
A.![]()
B. ![]()
C. ![]()
D. ![]()
giải bất
phương trình : ax+1/a-1>ax-1/a+1 với a>1
Giải bất phương trình với a là hằng số x + 1 a + a x > x + 2 a - 2 x
Điều kiện xác định: a ≠ 0.
Ta có: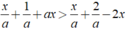
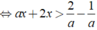
⇔ x( a + 2 ) > 1/a ( 1 )
+ Nếu a > - 2,a ≠ 0 thì nghiệm của bất phương trình là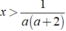
+ Nếu a < - 2 thì nghiệm của bất phương trình là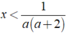
+ Nếu x = - 2 thì ( 1 ) có dạng 0x > - 1/2 luôn đúng với ∀ x ∈ R
Đúng 0
Bình luận (0)
Giải bất phương trình: (a - 2)*X+(aX+2)/a > 3/a - 2X
Pạn nào giải júp mik vs