a. Áp dụng đinh lí Py - ta - go vào Δ ABC vuông tại A:

   BC² = AC² + AB²

   BC² = 12² +  9² =  144 + 81 = 225

=> BC = 15 cm (BC > 0)

câu b mik chưa biết làm. Sorry bạn :(

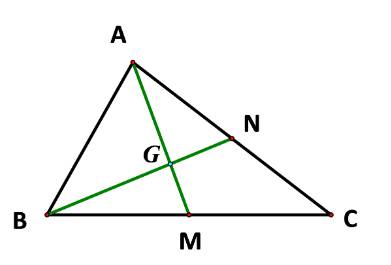
Ta có: \(\overrightarrow {AG} ,\overrightarrow {AM} \)là hai vecto cùng hướng và \(\left| {\overrightarrow {AG} } \right| = \frac{2}{3}\left| {\overrightarrow {AM} } \right|\)

Suy ra \(\overrightarrow {AG}  = \frac{2}{3}\overrightarrow {AM} .\) Vậy \(a = \frac{2}{3}.\)

Ta có: \(\overrightarrow {GN} ,\overrightarrow {GB} \)là hai vecto ngược hướng và \[\left| {\overrightarrow {GN} } \right| = \frac{1}{3}BN = \frac{1}{2}.\left( {\frac{2}{3}BN} \right) = \frac{1}{2}\left| {\overrightarrow {GB} } \right|\]

Suy ra \(\overrightarrow {GN}  =  - \frac{1}{2}\overrightarrow {GB} .\) Vậy \(b =  - \frac{1}{2}.\)

Xét ΔABC có

AM,CP,BN là trung tuyến

AM cắt CP cắt BN tại G

=>G là trọng tâm

=>BG=2/3BN; CG=2/3CP; AG=2/3AM

=>BK=KG=GN=1/3BN

=>GK=1/3BN; GM=1/3AM

Xet ΔBGC có BM/BC=BK/BG

nên MK//GC và MK/GC=BM/BC=1/2

=>MK=1/2GC=1/2*2/3*CP=1/3CP

a/

\(BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5cm\) (Pitago)

b/

Ta có

\(AM=\dfrac{BC}{2}=\dfrac{5}{2}=2,5cm\) (Trong tg vuông trung tuyến thuộc cạnh huyền thì bằng nửa cạnh huyền)

\(AG=\dfrac{2}{3}AM=\dfrac{2}{3}.\dfrac{5}{2}=\dfrac{5}{3}cm\)  (trong tg 3 đường trung tuyến đồng quy tại 1 điểm và điểm đó cách đỉnh 1 khoảng bằng 2/3 độ dài đường trung tuyến mà trung tuyến đó đi qua)

c/

Xét tg ABN và tg CDN có

AN=CN (gt); BN=DN (gt)

\(\widehat{ANB}=\widehat{CND}\) (Góc đối đỉnh)

=> tg ABN=tg CDN (c.g.c)=> \(\widehat{BAN}=\widehat{DCN}=90^o\Rightarrow CD\perp AC\)