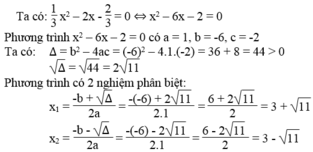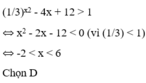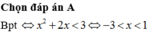Giải phương trình: 1.2x3 - 13x2 + 4 = 0

Những câu hỏi liên quan
Giải phương trình rồi kiểm nghiệm hệ thức vi-ét: 1 3 x 2 + 2 x - 16 3 = 0
Phương trình 1 3 x 2 + 2 x - 16 3 = 0 ⇔ x 2 +6x – 16 = 0 có hệ số a = 1, b = 6, c = -16
∆ '= 3 2 -1(-16) = 9 +16 =25 > 0
∆ ' = 25 =5
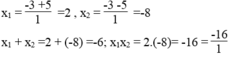
Đúng 0
Bình luận (0)
Xác định các hệ số a, b, c rồi giải phương trình : 1 3 x 2 - 2 x - 2 3 = 0
Giải phương trình
3
x
2
+
2
x
+
4
8
x
3
+
12
x
2
+
8
x
+
1
3...
Đọc tiếp
Giải phương trình 3 x 2 + 2 x + 4 = 8 x 3 + 12 x 2 + 8 x + 1 3 x 2 + 2 x + 5
Ta có: 3 x 2 + 2 x + 4 = 8 x 3 + 12 x 2 + 8 x + 1 3 x 2 + 2 x + 5 = ( 2 x + 1 ) 3 + 2 x + 1 3 x 2 + 2 x + 5 (1)
Dễ thấy 3 x 2 + 2 x + 4 > 0 với mọi x. Đặt u = 3 x 2 + 2 x + 4 v = 2 x + 1 .
Ta có: ( 1 ) ⇔ u = v 3 + v u 2 + 1 ⇔ u 3 + u = v 3 + v ⇔ ( u − v ) ( u 2 + u v + v 2 + 1 ) = 0 ⇔ u = v
(Vì u 2 + u v + v 2 + 1 = u + v 2 2 + 3 4 v 2 + 1 > 0 )
u = v ⇔ 3 x 2 + 2 x + 4 = 2 x + 1 ⇒ 3 x 2 + 2 x + 4 = 4 x 2 + 4 x + 1 x 2 − 2 x − 3 = 0 ⇒ x = 3 h o a c x = − 1.
Thử lại, ta nhận x= 3
Đúng 0
Bình luận (0)
Giải bất phương trình 1 3 x 2 - 4 x - 12 > 1
A. x < -6 hoặc x > 2
B. -6 < x < 2
C. x < -2 hoặc x > 6
D. -2 < x < 6
Tập nghiệm của phương trình
x
+
1
3
x
2
-
3
0
là: A.
S
-
1
3
;
6
B.
S
-
1...
Đọc tiếp
Tập nghiệm của phương trình x + 1 3 x 2 - 3 = 0 là:
A. S = - 1 3 ; 6
B. S = - 1 3 ; 3
C. S = 1 3 ; 3
D. S = 1 3 ; - 3
Tính nhẩm nghiệm của các phương trình: 1 3 x 2 - 3 2 x - 11 6 = 0
⇔ 2 x 2 - 9x - 11 = 0 có hệ số a = 2, b = -9, c = -11
Ta có: a –b +c =2 – (-9) +(-11) =0
Suy ra nghiệm của phương trình là x 1 =-1 , x 2 = -c/a = -(-11)/2 =11/2
Đúng 0
Bình luận (0)
Tính biệt thức từ đó tìm số nghiệm của phương trình
−
13
x
2
+
22
x
−
13
0
A.
∆
654 và phương trình có nghiệm kép B.
∆
−192 và phương trình vô nghiệm C.
∆
− 654 và phương trình vô nghiệm D.
∆
− 654 và phương trình có hai nghiệm phân biệt
Đọc tiếp
Tính biệt thức từ đó tìm số nghiệm của phương trình − 13 x 2 + 22 x − 13 = 0
A. ∆ = 654 và phương trình có nghiệm kép
B. ∆ = −192 và phương trình vô nghiệm
C. ∆ = − 654 và phương trình vô nghiệm
D. ∆ = − 654 và phương trình có hai nghiệm phân biệt
Ta có:
−13x2 + 22x − 13 = 0 (a = −13; b = 22; x = −13)
⇒ ∆ = b2 – 4ac = 222 – 4.(−13). (−13) = −192 < 0
nên phương trình vô nghiệm
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Tập nghiệm của bất phương trình 1 3 x 2 + 2 x > 1 27 là
A. -3 < x < 1
B. 1 < x < 3
C. -1 < x < 3
D. x < -3; x > 1
Số nghiệm nguyên của bất phương trình
1
3
x
2
-
3
x
-
10
1
3
x
-
2
là? A. 1 B. 8 C. 9 D. 10
Đọc tiếp
Số nghiệm nguyên của bất phương trình 1 3 x 2 - 3 x - 10 > 1 3 x - 2 là?
A. 1
B. 8
C. 9
D. 10
Tập nghiệm của hệ phương trình
x
+
y
+
x
y
-
13
x
2
+
y
2...
Đọc tiếp
Tập nghiệm của hệ phương trình x + y + x y = - 13 x 2 + y 2 - x - y = 32 là:
A. - 5 ; 2 ; 5 ; - 3
B. - 5 ; 2 ; 5 ; - 3 ; - 3 ; 5
C. - 5 ; 2 ; - 2 ; 5 ; 5 ; - 3 ; - 3 ; 5
D. - 5 ; 2 ; 2 ; - 5 ; 5 ; - 3 ; - 3 ; 5
t 2
Ta có: x + y + x y = - 13 x 2 + y 2 - x - y = 32 ⇔ x + y + x y = - 13 ( x + y ) 2 - 2 x y - ( x + y ) = 32
Đặt S = x+ y; P = xy . Khi đó, hệ phương trình trên trở thành:
S + P = - 13 ( 1 ) S 2 - 2 P - S = 32 ( 2 )
Từ (1) suy ra: P = -S – 13 thay vào (2) ta được:
S 2 – 2(-S – 13) – S = 32
⇔ S 2 + 2 S + 26 - S - 32 = 0 ⇔ S 2 + S - 6 = 0 ⇔ [ S = 2 S = - 3
* Với S = 2 thì P = -15 . Khi đó , x và y là nghiệm phương trình:
t 2 - 2t – 15 = 0 ⇔ [ t = 5 t = - 3
* Với S = -3 thì P = -10. Khi đó, x và y là nghiệm phương trình:
t 2 + 3t – 10 =0 ⇔ [ t = 2 t = - 5
Vậy hệ phương trình đã cho có 4 nghiệm ( 5; -3); (-3; 5); (2; -5); (-5; 2).
Chọn D.
Đúng 0
Bình luận (0)