Chứng tỏ rằng tỉ số chu vi của hai tam giác đồng dạng bằng tỉ số đồng dạng.

Những câu hỏi liên quan
chứng tỏ :
tỉ số chu vi của 2 tam giác động dạng bằng tỉ số đồng dạng
Cho\(\Delta ABC~\Delta DEF\) với tỉ số đồng dạng:\(\frac{3}{2}\)
Vì\(\Delta ABC~DEF\) theo tỉ số\(\frac{3}{2}\) nên ta có:
\(\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}=\frac{3}{2}\)
Theo tính chất dãy tỉ số bằng nhau ta có:
\(\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}=\frac{AB+AC+BC}{DE+DF+EF}=\frac{3}{2}\)
Suy ra:\(\frac{AB+AC+BC}{DE+DF+EF}=\frac{3}{2}\)
Vậy \(\frac{P_{ABC}}{P_{DEF}}=\frac{3}{2}\)
Hay tỉ số chu vi của 2 tam giác đồng dạng bằng nhau
P:chu vi
#hoktot<3#
Cho hai tam giác A'B'C' và ABC đồng dạng với nhau theo tỉ số k. Chứng minh rằng tỉ số chu vi của hai tam giác cũng bằng k ?
Cho hai tam giác ABC và A'B'C' đồng dạng với nhau theo tỉ số k, chứng minh rằng tỉ số chu vi của hai tam giác ABC và A'B'C' cũng bằng k
Sử dụng tính chất dãy tỉ số bằng nhau để chứng minh
Đúng 0
Bình luận (0)
Cho hai tam giác A'B'C' và ABC đồng dạng với nhau theo tỉ số k. Chứng minh rằng tỉ số hai chu vi tam giác cũng bằng k.
Vì △ A'B'C' đồng dạng △ ABC theo tỉ số k nên ta có:
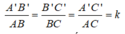
Theo tính chất dãy tỉ số bằng nhau, ta có:
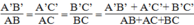
Suy ra: 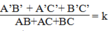
Vậy 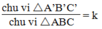
Đúng 0
Bình luận (0)
Cho hai tam giác A'B'C' và ABC đồng dạng với nhau theo tỉ số k. Chứng minh rằng tỉ số hai chu vi tam giác cũng bằng k.
Chứng minh tỉ số 2 chu vi của 2 tam giác đồng dạng bằng tỉ số đồng dạng
Gọi chu vi của tam giác ABC là C1, chu vi của tam giác DEF là C2
và ΔABC∼ΔDEF
=>AB/DE=BC/EF=AC/DF
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AB}{DE}=\dfrac{BC}{EF}=\dfrac{AC}{DF}=\dfrac{AB+BC+AC}{DE+EF+DF}=\dfrac{C_1}{C_2}\)
Do đó: Tỉ số chu vi bằng tỉ số đồng dạng
Đúng 0
Bình luận (0)
1. Hai tam giác ABC và DEF có: AB 12cm, BC 9cm, CA 15cm, DE 16, EF 12cm, FD 20cm
a) Chứng minh hai tam giác này đồng dạng
b) Viết các cặp góc bằng nhau
2. a) Chứng tỏ rằng tỉ số các chu vi của hai tam giác đồng dạng bằng tỉ số đồng dạng
b) Cho ΔABC và ΔABC đồng dạng theo tỉ số k frac{2}{7} . Biết rằng tồng chu vi của hai tam giác bằng 180m. Tính chu vi của mỗi tam giác
Đọc tiếp
1. Hai tam giác ABC và DEF có: AB = 12cm, BC = 9cm, CA = 15cm, DE = 16, EF = 12cm, FD = 20cm
a) Chứng minh hai tam giác này đồng dạng
b) Viết các cặp góc bằng nhau
2. a) Chứng tỏ rằng tỉ số các chu vi của hai tam giác đồng dạng bằng tỉ số đồng dạng
b) Cho ΔABC và ΔA'B'C' đồng dạng theo tỉ số k = \(\frac{2}{7}\) . Biết rằng tồng chu vi của hai tam giác bằng 180m. Tính chu vi của mỗi tam giác
1/
Ta có: \(\frac{12}{16}=\frac{9}{12}=\frac{15}{20}=\frac{3}{4}\Leftrightarrow\frac{AB}{DE}=\frac{BC}{EF}=\frac{CA}{FD}\)
suy ra Tam giác ABC đồng dạng với tam giác DEF
Nên \(\left\{{}\begin{matrix}\widehat{ABC}=\widehat{DEF}\\\widehat{ACB}=\widehat{DFE}\\\widehat{BAC}=\widehat{EDF}\end{matrix}\right.\) (2 góc tương ứng)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh rằng tỉ số hai bán kính của hai đường tròn ngoại tiếp hai tam giác đồng dạng bằng tỉ số đồng dạng
AB/sinC=2R
A'B'/sinC'=2R'
mà AB/A'B'=k
và goc C=góc C'
nên 2R/2R'=AB/A'B'=k
=>R/R'=k(Đpcm)
Đúng 0
Bình luận (0)
Cho 2 tam giác a'b'c' và abc đồng dạng theo tỉ số k. Chứng minh rằng tỉ số 2 chu vi tam giác cũng bằng k.


























