Cho △ABC vuông tại A, BI là đường phân giác (I∈AC). Kẻ CH vuông góc với đường thẳng BI (H∈BI)
a. Chứng minh: △ABI đồng dạng với △HCI.
b. Chứng minh: IBC = ICH.
c. Cho biết AB = 3cm, AC = 4cm. Tính độ dài các cạnh AI, IC.
Cho tam giác ABC vuông tại A, Bi là đường phân giác,I thuộc AC kẻ CH vuông với đường thẳng BI, H thuộc AC.
a,Chứng minh tam giác ABI đồng dạng tam giác HCI
b,Chứng ming góc IBC=góc ICH
Cho tam giác ABC vuông tại A ,BI là đường phân giác (I thuộc AC ) . Kẻ CH vuông góc với đường thẳng BI (H thuộc BI)
a) Chứng minh tam giác ABI đồng dạng với tam giác HCI
b) chứng minh tam giác BHC đồng dạng với tam giác CHI
c)Cho biết AB=6cm , AC=8cm . Tính độ dài các cạnh AI , IC
Cho tam giác ABC vuông tại A, BI là đường phân giác( I thuộc AC). Kẻ CH vuông góc với BI ( H thuộc BI)
A, cm tam giác ABI đồng dạng với tam giác HCI
B, cm : góc IBC = góc ICH
C, biết AB = 6cm ; AC= 8cm ; tính độ dài AI; IC
Cho tam giác ABC vuông góc tại A, BI là đường phan giác ( I thuộc AC ) . Kẻ CK vông góc với BI( K thuộc BI)
a) Chứng minh ∆ ABI đồng dạng ∆ KCI
b) Chứng minh góc IBC = góc ICK
c) Cho biết AB = 3cm,AC =4cm.Tính độ dài của cạnh AI,IC
a,Xét tam giác ABI và tam giác KCI có
góc AIB = góc KIC (đối đỉnh)
góc BAI = góc IKC ( = 90 độ )
=> ABI ~ KCI
b,Từ hai tam giác trên động dạng với nhau,ta suy ra : góc ABI = góc ICK (1)
Mặ khác,BI là phân giác góc ABC nên ABI = góc IBC (2)
Từ (1) và (2) => Góc IBC = góc ICK
c,AB = 3,AB=4 => BC=5(định lý Pytago)
AB:BC=AI:IC(tính chất đường phân giác)
=>AB:(AB+BC) = AI:(AI+IC)=AI:AC
=> 3:8 =AI: 4 => AI = 1,5
IC=AC-AI => IC = 4 - 1,5= 2,5.
Cho tam giác ABC vuông tại A có :AB=6cm; BC=8cm. BI là đường phân giác của góc B(I thuộc AC). Kẻ Ch vuông góc với đường thẳng BI (H thuộc BI)
a.Tính độ dài các cạnh AI,IC
b.C/m: Tam giác ABI đồng dạng với tam giác HCI,từ đó=>AB.CI=HC.BI
c. Tính diện tích HCI
a: Sửa đề: AC=8cm
BC=căn 6^2+8^2=10cm
Xét ΔBAC có BI là phân giác
nên AI/BA=CI/BC
=>AI/3=CI/5=(AI+CI)/(3+5)=8/8=1
=>AI=3cm; CI=5cm
b: Xét ΔABI vuông tại A và ΔHCI vuông tại H có
góc AIB=góc HIC
=>ΔABI đồng dạng với ΔHCI
=>AB/HC=BI/CI
=>AB*CI=BI*HC
Cho tam giác ABC vuông tại A. BI là đường phân giác( I thuộc AC). Kẻ CH vuông góc với đường thẳng BI ( H thuộc BI).
a) Chứng minh tam giác ABI đồng dạng với tam giác HCI.
b) Chứng minh góc IBC = góc ICH
c) Cho AB=6cm, AC= 8cm. Tính AI, IC.
EM ĐANG CẦN GẤP. MN GIÚP EM VỚI NHA Ạ. E CẢM ƠN Ạ.
a) Xét ΔABI và ΔHCI
∠A=∠H=900
∠BIA=∠HIC(đối đỉnh)
⇒ΔABI \(\sim\)ΔHCI(g-g)
b)ta có :ΔABI \(\sim\)ΔHCI(cmt)
⇒∠ABI = ∠ICH(2 góc tương ứng )
Mà ∠ABI = ∠IBC(BI là tia phân giác ∠B)
⇒∠IBC = ∠ICH
c)Xét ΔABC vuông tại A
Nên theo định lí Pi-ta-go ta có :
\(BC^2=AB^2+AC^2\)
\(BC^2=6^2+8^2\)
\(BC^2=36+64\)
\(BC^2=100\)
\(BC=\sqrt{100}=10\)
Ta có :BI là tia phân giác ∠B
Nên theo tính chất tia phân giác
\(\frac{IA}{AB}=\frac{CI}{AC}\)
theo tính chất dãy tỉ số bằng nhau
\(\frac{AI}{AB}=\frac{IC}{BC}=\frac{AI+IC}{AB+BC}=\frac{AC}{6+10}=\frac{8}{16}=\frac{1}{2}\)
*\(\frac{AI}{AB}=\frac{1}{2}\Rightarrow AI=AB\cdot\frac{1}{2}=6\cdot\frac{1}{2}=3\)
*\(\frac{IC}{BC}=\frac{1}{2}\Rightarrow IC=BC\cdot\frac{1}{2}=10\cdot\frac{1}{2}=5\)
Cho tam giác ABC vuông tại A,BI là đường phân giác ( I thuộc AC) kẻ CH vuông với BI (H thuộc BI)
a) chứng minh tam giác ABI đồng dạng tam giác HCI
b) chứng minh góc IBC = góc ICH. Tính các cạnh AI,IC
A)XÉT TAM GIÁC ABI VÀ TAM GIÁC HCI CÓ ;
GÓC A =GÓC CHI (=90 ĐỘ )
GÓC AIB=GÓC HIC (ĐỐI ĐỈNH )
=>TAM GIÁC ABI ĐỒNG DẠNG VỚI TAM HCI (G.G)
B)VÌ TAM GIÁC ABI ĐỒNG DẠNG VỚI TAM GIÁC HCI (THEO CÂU A)
=>GÓC ABI=GÓC HCI (1)
MÀ GÓC ABI BẰNG GÓC CBI(VÌ BI LÀ TIA PHÂN GIÁC ) (2)
TỪ (1) VÀ (2) =>GÓC HCI BĂNG GÓC CBI (DPCM)
Cho ▲ABC vuông tại A, BI là phân giác, kẻ CH vuông góc BI
a)Cho AB=6cm, AC=8cm. Tính AI,IC.
b)Chứng minh:▲ABI đồng dạng với ▲HCI
c)chứng minh:▲BHC đồng dạng với ▲CHI. Tính tỉ số diện tích của 2 ▲.
b) Xét \(\Delta\)ABI vuông tại A và \(\Delta\)HCI vuông tại H có
\(\widehat{AIB}=\widehat{HIC}\)(hai góc đối đỉnh)
Do đó: \(\Delta\)ABI\(\sim\)\(\Delta\)HCI(g-g)
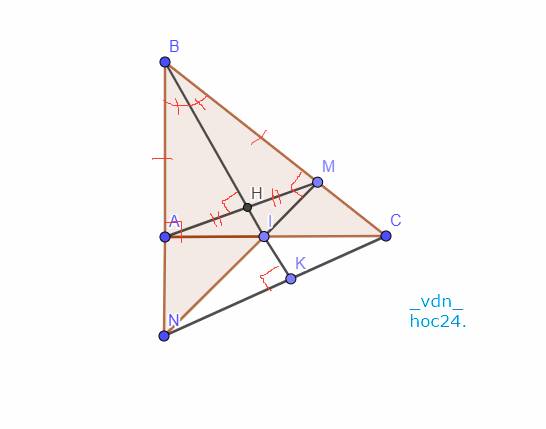
Cho Δ ABC vuông tại A, đường phân giác BI (I ∈ AC). Kẻ IM vuông góc với BC ( M ∈ BC). Gọi N là giao điểm của AB và IM.
a) Chứng minh: Δ ABI =Δ MBI và BI là đường trung trực của đoạn thẳng AM
b) Chứng minh IN = IC
c) Chứng minh BI vuông góc với NC
\(\text{#TNam}\)
`a,`
Xét Tam giác `ABI` và Tam giác `MBI` có:
`\text {BI chung}`
\(\widehat{ABI}=\widehat{MBI} (\text {tia phân giác}\) \(\widehat{ABM} )\)
\(\widehat{BAI}=\widehat{BMI}=90^0\)
`=> \text {Tam giác ABI = Tam giác MBI (ch-gn)}`
`=> BA = BM (\text {2 cạnh tương ứng})`
Gọi `H` là giao điểm của `BI` với `AM`
Xét Tam giác `HAB` và Tam giác `HMB` có:
\(\text{BA = BM (CMT)}\)
\(\widehat{ABH}=\widehat{MBH} (\text {tia phân giác} \widehat{ABM})\)
`\text {BH chung}`
`=> \text {Tam giác HAB = Tam giác HMB (c-g-c)}`
`-> \text {HA = HM (2 cạnh tương ứng)}`
`->`\(\widehat{BHA}=\widehat{BHM} (\text {2 góc tương ứng})\)
Mà `2` góc này nằm ở vị trí kề bù
`->`\(\widehat{BHA}+\widehat{BHM}=180^0\)
`->`\(\widehat{BHA}=\widehat{BHM}=\)`180/2=90^0`
`-> \text {BH} \bot \text {AM}`
Ta có: \(\left\{{}\begin{matrix}BH\perp AM\\HA=HM\end{matrix}\right.\)
`->` \(\text{BI là đường trung trực của AM.}\)
`b,`
Xét Tam giác `BAC` và Tam giác `BMN` có:
\(\widehat{B} \) `\text {chung}`
`BA = BM (a)`
\(\widehat{BAC}=\widehat{BMN}=90^0\)
`=> \text {Tam giác BAC = Tam giác BMN (g-c-g)}`
`-> \text {BN = BC (2 cạnh tương ứng)}`
Xét Tam giác `BIN` và Tam giác `BIC` có:
`BN = BC (CMT)`
\(\widehat{NBI}=\widehat{CBI} (\text {tia phân giác} \widehat{NBC})\)
`\text {BI chung}`
`=> \text {Tam giác BIN = Tam giác BIC (c-g-c)}`
`-> \text {IN = IC (2 cạnh tương ứng)}`
`c,`
Gọi `K` là giao điểm của `BI` và `NC`
Xét Tam giác `NBK` và Tam giác `CBK` có:
`BN = BC (CMT)`
\(\widehat{NBK}=\widehat{CBK} (\text {tia phân giác} \widehat{NBC})\)
`\text {BK chung}`
`=> \text {Tam giác NBK = Tam giác CBK (c-g-c)}`
`->`\(\widehat{BKN}=\widehat{BKC} (\text {2 góc tương ứng})\)
Mà `2` góc này nằm ở vị trí kề bù
`->`\(\widehat{BKN}+\widehat{BKC}=180^0\)
`->`\(\widehat{BKN}=\widehat{BKC}=\)`180/2=90^0`
`-> \text {BK} \bot \text {NC}`
`-> \text {BI} \bot \text {NC (đpcm)}`