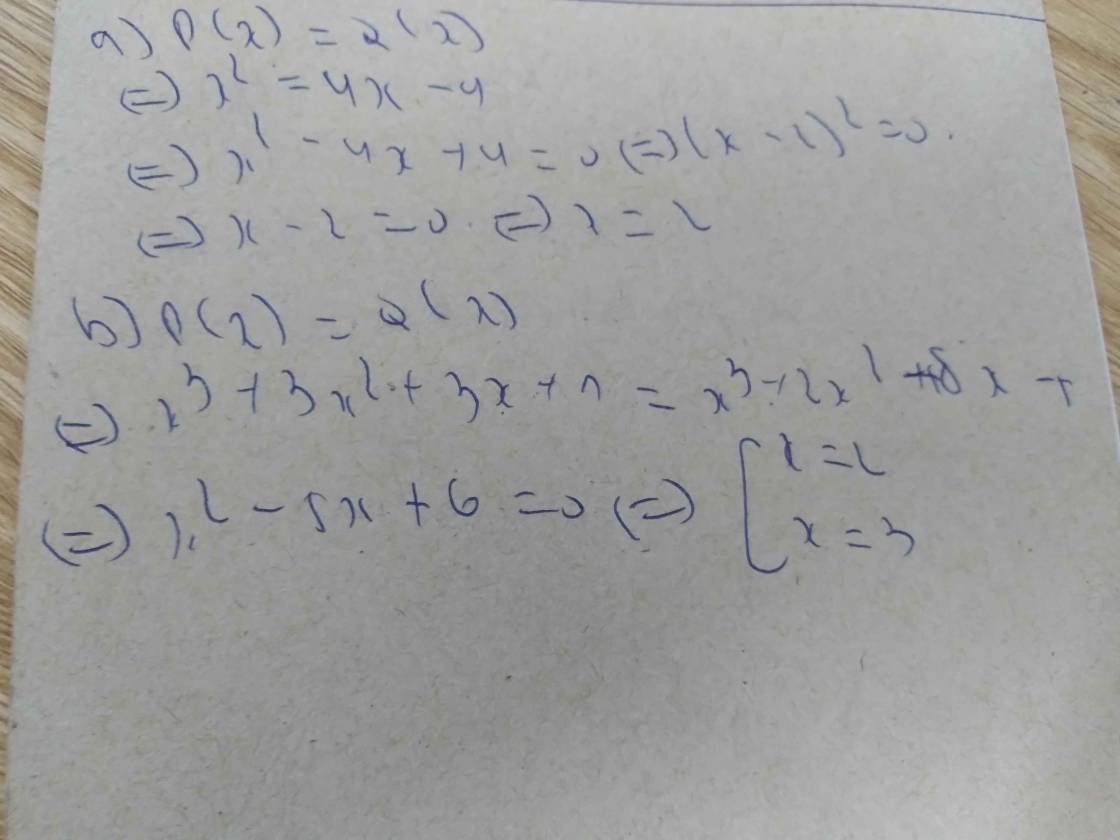Cho đa thức f(x) =x3-3x2+3x-4.Với giá trị nguyên nào của x thì giá trị của đa thức f(x) chia hết cho giá trị của đa thức x2+2

Những câu hỏi liên quan
Cho đa thức f(x) =x3-3x2+3x-4.Với giá trị nguyên nào của x thì giá trị của đa thức f(x) chia hết cho giá trị của đa thức x2+2
x3-3x2+3x-4 x2+2
x3 +2x x-3
_____________
-3x2+x-4
-3x2 -6
_____________
x+2
-Để f(x) chia hết cho đa thức x2+2 thì:
\(x+2=0\Leftrightarrow x=2\)(nhận)
Đúng 0
Bình luận (0)
Cho đa thức \(f\left(x\right)=x^3-3x^2+3x-4\). Với giá trị nguyên nào của x thì giá trị đa thức f(x) chia hết cho giá trị của đa thức \(x^2+2\)
a) cho 2 đa thức P(x)=x2 và đa thức Q(x)=4x-4. với giá trị nào của x thì P(x)=Q(x)
b) a) cho 2 đa thức P(x)=x3+3x2+3x+1 và đa thức Q(x)=x3+2x2+8x-5. với giá trị nào của x thì P(x)=Q(x)Cho đa thức A=x3 + 3x2 + 3x -2 và đa thức B= x+1
a) Thực hiện phép chia đa thức A cho đa thức B.
b) Tìm các giá trị nguyên của x để giá trị của đa thức A chia hết cho giá trị của đa thức B.
a: \(\dfrac{A}{B}=\dfrac{x^3+x^2+2x^2+2x+x+1-3}{x+1}=x^2+2x+1-\dfrac{3}{x+1}\)
b: Để A chia hết cho B thì \(x+1\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{0;-2;2;-4\right\}\)
Đúng 1
Bình luận (0)
Cho đa thức f(x)= x3+3x2+2x
a)phân tích các đa thức f(x) thành nhân tử
b) Tìm x để đa thức f(x)=0
c)tìm x nguyên để giá trị của đa thức f(x) chia hết cho x+3.
a. x3+x2+2x2+2x
= (x3+x2)+(2x2+2x)
= x2(x+1)+2x(x+1)
= (x2+2x)(x+1)
= x(x+2)(x+1)
Đúng 0
Bình luận (0)
Cho đa thức f(x)=x^3-3x^2+2. Với giá trị nguyên nào của a và b thì đa thức f(x) chia hết cho đa thức x^2+ax+b
và đây là cách phân tích duy nhất mà các hệ số của nhân tử đều nguyên.
Do đó f(x) cho hết khi chia hết
Đúng 2
Bình luận (1)
Ta có:
\(f\left(x\right)=\left(x-1\right)\left(x^2-x-2\right)\) và đây là cách phân tích duy nhất mà các hệ số của nhân tử đều nguyên
Do đó f(x) cho hết \(x^2+ax+b\) khi \(x^2-2x-2\) chia hết \(x^2+ax+b\)
=>a=b= -2
Đúng 2
Bình luận (0)
Cho đa thức f(x)=x^3-3x^2+2. Với giá trị nguyên nào của a và b thì đa thức f(x) chia hết cho đa thức x^2+ax+b
\(f\left(x\right)=\left(x-1\right)\left(x^2-2x-2\right)\) và đây là cách phân tích duy nhất mà các hệ số của nhân tử đều nguyên
Do đó f(x) cho hết \(x^2+ax+b\) khi \(x^2-2x-2\) chia hết \(x^2+ax+b\)
\(\Rightarrow a=b=-2\)
Đúng 3
Bình luận (0)
Cho đa thức: \(f\left(x\right)=x^3-3x^2+2\). Với giá trị nguyên nào của a và b thì đa thức f(x) chia hết cho đa thức: \(x^2+ax+b\)
Lời giải:
\(x^3-3x^2+2=x(x^2+ax+b)-(a+3)(x^2+ax+b)+(a^2+3a-b)x+b(a+3)+2\)
Để $f(x)$ chia hết cho $x^2+ax+b$ thì:
\(\left\{\begin{matrix} a^2+3a-b=0\\ b(a+3)+2=0\end{matrix}\right.\)
Với $a,b$ nguyên ta dễ dàng tìm được $a=b=-2$
Đúng 1
Bình luận (0)
1, Tìm các số nguyên x,y thỏa mãn: x2 + 2xy + 7(x+y) +2y2 +10 = 0
2, Cho đa thức f(x) = x3-3x2+3x-4. Với giá trị nguyên nào của x thì giá trị của đa thức f(x) chia hết cho giá trị của đa thức x2 + 2.
mình cần gấpppppppppppppppppppppp, giúp với ạ
Bài 3. Tìm giá trị của a, b để đa thức f(x) chia hết cho đa thức g(x) với
f(x) = x4− 3x3+ 3x2+ ax + b; g(x) = x2− 3x + 4.
\(f\left(x\right)⋮g\left(x\right)\)
\(\Leftrightarrow x^4-3x^3+4x^2-x^2+3x-4+\left(a-3\right)x+\left(b+4\right)⋮x^2-3x+4\)
\(\Leftrightarrow\left(a,b\right)=\left(3;-4\right)\)
Đúng 0
Bình luận (0)