tinh diện tich hình bình hành ABCD , bt \(\widehat{A}\) = \(^{^{ }}45^o\)
AB = 8cm , AD= 10cm
Những câu hỏi liên quan
Bài 4. Cho hình bình hành ABCD có chu vi bằng 60cm, cạnh đáy AB lớn hơn cạnh AD là 10cm, chiều cao DH là 8cm . Tính diện tích hình bình hành ABCD.
\(S_{ABCD}=AB\cdot DH=8\cdot\left(30-10\right)=8\cdot20=160\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có cạnh AB = 10 3 c m , AD = 8cm, A ^ = 60°. Tính diện tích của hình bình hành
Kẻ DH ^ AB tại H
⇒ A H = A D 2 = 4 c m
Áp dụng định lý Pytago trong D vuông ADH Þ DH = 4 3 cm.
ÞSABCD = DH.AB = 120cm2
Đúng 0
Bình luận (0)
cho hình bình hành ABCD (AB<BC) BC=8cm, AB=5cm, kẻ BH vuông góc AD có AH=3cm.
tính diện tích của hình bình hành đó
cho hình bình hành abcd, mbcn. tinh dien tich hinh binh hanh abcd, biet S hinh binh hanh mbcn la 8cm vuong va ab=3*mb
VŨ HUY KHOA 2xy+x+y=23
\(\Leftrightarrow4xy+2x+2y=46\)
\(\Leftrightarrow2x\left(2y+1\right)+2y+1=47\)
\(\Leftrightarrow\left(2x+1\right)\left(2y+1\right)=47\)
\(\Rightarrow2x+1\inƯ\left(47\right)=\left\{\pm1;\pm47\right\}\)
Đúng 0
Bình luận (0)
tính diện tích hình bình hành ABCD có S=30cm2 , AB=10cm,AD=6cm,góc A >góc B
Cho hình bình hành ABCD, AB= 10cm, AD= 6cm, góc A > góc B. Tính số đo các góc của hình bình hành ABCD.
mình dốt hình lắm chỉ biết số học thôi
CHÚC BẠN HỌC GIỎI
TK MÌNH NHÉ
Đúng 0
Bình luận (0)
Cho hình bình hành abcd có góc a = 45 độ, ab=bd=18cm
a) tính ad
b) tính diện tích abcd
Cho hình bình hành ABCD có AB = 4, AD = 6, \(\widehat {BAD} = {60^o}\) (Hình 73).
a) Biểu thị các vecto \(\overrightarrow {BD} ,\overrightarrow {AC} \) theo \(\overrightarrow {AB} ,\overrightarrow {AD} .\)
b) Tính các tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AD} ,\;\overrightarrow {AB} .\overrightarrow {AC} ,\;\overrightarrow {BD} .\overrightarrow {AC} .\)
c) Tính độ dài các đường chéo \(BD,AC.\)
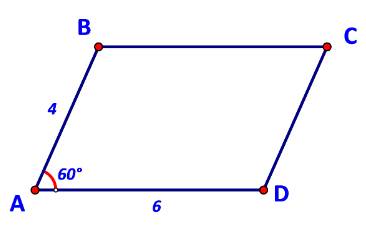
a) \(\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} ;\;\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} .\)
b) \(\overrightarrow {AB} .\overrightarrow {AD} = 4.6.\cos \widehat {BAD} = 24.\cos {60^o} = 12.\)
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} (\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD} = {4^2} + 12 = 28.\\\overrightarrow {BD} .\overrightarrow {AC} = (\overrightarrow {AD} - \overrightarrow {AB} )(\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AD} ^2} - {\overrightarrow {AB} ^2} = {6^2} - {4^2} = 20.\end{array}\)
c) Áp dụng định lí cosin cho tam giác ABD ta có:
\(\begin{array}{l}\quad \;B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos A\\ \Leftrightarrow B{D^2} = {4^2} + {6^2} - 2.4.6.\cos {60^o} = 28\\ \Leftrightarrow BD = 2\sqrt 7 .\end{array}\)
Áp dụng định lí cosin cho tam giác ABC ta có:
\(\begin{array}{l}\quad \;A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {4^2} + {6^2} - 2.4.6.\cos {120^o} = 76\\ \Leftrightarrow AC = 2\sqrt {19} .\end{array}\)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có góc D=30độ , AD=8cm , DC=7.5cm. Tính diện tích hình bình hành ABCD?
