Tìm giá trị m để phương trình có nghiệm : 3sin(-x) +4cosx +1 =m

Những câu hỏi liên quan
Cho phương trình : cos2x+4cosx+m=0 . Tìm tẩ cả các giá trị tham số m để phương trình đã cho có nghiệm
\(\Leftrightarrow2cos^2x+4cosx-1=-m\)
Xét \(f\left(x\right)=2cos^2x+4cosx-1\)
\(f\left(x\right)=2cos^2x+4cosx+2-3=2\left(cosx+1\right)^2-3\ge-3\)
\(f\left(x\right)=2cos^2x+4cosx-6+5=2\left(cosx-1\right)\left(cosx+3\right)+5\le5\)
\(\Rightarrow-3\le-m\le5\Rightarrow-5\le m\le3\)
Đúng 3
Bình luận (0)
Có bao nhiêu giá trị nguyên của m để phương trình cos2x-4cosx-m 0 có nghiệm A. 6 B. 7 C. 9 D. 8
Đọc tiếp
Có bao nhiêu giá trị nguyên của m để phương trình cos2x-4cosx-m= 0 có nghiệm
A. 6
B. 7
C. 9
D. 8
Có bao nhiêu giá trị nguyên của m để phương trình cos 2 x − 4 cos x − m = 0 có nghiệm.
A. 6
B. 7
C. 8
D. 9
Đáp án D
Ta có: P T ⇔ 2 cos 2 x − 1 − 4 cos x = m
→ t − cos x f t = 2 t 2 − 4 t − 1 = m t ∈ − 1 ; 1
Khi đó: f ' t = 4 t − 4 = 0 ⇔ t = 1
Lại có: f 1 = 5 ; f 1 = − 3 do đó PT đã cho có nghiệm
⇔ m ∈ − 3 ; 5 ⇒ có 9 giá trị nguyên của m
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của m để phương trình
cos
2
x
−
4
cos
x
−
m
0
có nghiệm A. 6 B. 7 C. 9 D. 8
Đọc tiếp
Có bao nhiêu giá trị nguyên của m để phương trình cos 2 x − 4 cos x − m = 0 có nghiệm
A. 6
B. 7
C. 9
D. 8
Đáp án C
Ta có
cos 2 x − 4 cos x − m = 0 ⇔ 2 cos 2 x − 1 − 4 cos x − m = 0 ⇔ 2 cos 2 x − 4 cos x − 1 = m *
Đặt t = cos x ∈ − 1 ; 1 , khi đó * ⇔ m = f t = 2 t 2 − 4 t − 1 I .
Suy ra f t là hàm số nghịch biến trên − 1 ; 1 nên để I có nghiệm − 3 ≤ m ≤ 5
Vậy có tất cả 9 giá trị nguyên của tham số m cần tìm
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để phương trình m + 3 m + 3 sin x 3 3 = sin x có nghiệm thực ?
A. 5
B. 7
C. 3
D. 2
Đáp án A
*Phương trình m + 3 m + 3 sin x 3 3 = sin x ⇔ m + 3 m + 3 sin x 3 = sin 3 x
⇔ ( m + 3 sin x ) + 3 m + 3 sin x 3 = sin 3 x + 3 sin x ( 1 )
* Xét hàm số f ( t ) = t 3 + 3 t trên ℝ . Ta có f ' ( t ) = 3 t 2 + 3 > 0 ∀ t ∈ ℝ nên hàm số f(t) đồng biến trên ℝ .
Suy ra (1) f 3 + 3 sin x 3 f ( sin x ) ⇔ 3 + 3 sin x 3 = sin x
Đặt sin x = t, t ∈ [ - 1 ; 1 ] Phương trình trở thành t 3 - 3 t = m
* Xét hàm số g(t) trên t ∈ - 1 ; 1 Ta có g ' ( t ) = 3 t 2 - 3 ≤ 0 , ∀ t ∈ [ - 1 ; 1 ] và g ' ( t ) = 0 ⇔ t = ± 1 Suy ra hàm số g(t) nghịch biến trên [-1;1]
* Để phương trình có nghiệm đã cho có nghiệm thực ⇔ Phương trình t 3 - 3 t = m có nghiệm trên [-1;1]
m i n [ - 1 ; 1 ] g ( t ) ≤ m ≤ m a x [ - 1 ; 1 ] g ( t ) ⇔ g ( 1 ) ≤ m ≤ g ( - 1 ) ⇔ - 2 ≤ m ≤ 2
Vậy có 5 giá trị nguyên của m thỏa mãn là m ∈ - 2 ; - 1 ; 0 ; 1 ; 2
Đúng 0
Bình luận (0)
Cho phương trình m . sin x + 4 cos x = 2 m − 5 với m là tham số. Có bao nhiêu giá trị nguyên của m để phương trình có nghiệm?
A. 4.
B. 7.
C. 6.
D. 5.
Đáp án C.
Áp dụng bất đẳng thức Bunhiacopxki, ta có:
m . s inx+4cosx 2 ≤ m 2 + 4 2 sin 2 x + c os 2 x = m 2 + 16.
Nên để phương trình đã cho có nghiệm ⇔ 3 m − 5 2 ≤ m 2 + 16 ⇔ 3 m 2 20 m + 9 ≤ 0.
Kết hợp với m ∈ ℤ , ta được m = 1 ; 2 ; 3 ; 4 ; 5 ; 6 là giá trị cần tìm.
Đúng 0
Bình luận (0)
Tổng tất cả các giá trị nguyên của m để phương trình 4 sin x + m - 4 cos x - 2 m + 5 = 0 có nghiệm là
A. 5
B. 6
C. 10
D. 3
Cho hàm số yf(x) có đồ thị như hình bên dưới.Có bao nhiêu giá trị nguyên của tham số m để phương trình f(3sinx + 4cosx) f(m) có nghiệm? A. 10 B. 14. C. 9 D. 11.
Đọc tiếp
Cho hàm số y=f(x) có đồ thị như hình bên dưới.
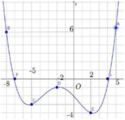
Có bao nhiêu giá trị nguyên của tham số m để phương trình f(3sinx + 4cosx) = f(m) có nghiệm?
A. 10
B. 14.
C. 9
D. 11.
1,phương trình 3sin(2x-η/5)+1=m có nghiệm khi m∈(a,b).Giá trị b-a là
\(3sin\left(2x-\dfrac{\pi}{5}\right)+1=m\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{5}\right)=\dfrac{m-1}{3}\)
Phương trình có nghiệm khi:
\(-1\le\dfrac{m-1}{3}\le1\)
\(\Leftrightarrow-2\le m\le4\)
\(\Rightarrow m\in\left[-2;4\right]\)
\(\Rightarrow b-a=6\)
Đúng 0
Bình luận (0)











