Giải phương trình :
(3x-2)(3x-1)=(3x+1)
1.Giải các phương trình sau : a,7x+35=0 b, 8-x/x-7 -8 =1/x-7 2.giải bất phương trình sau : 18-3x(1-x)_< 3x^2-3x
a: 7x+35=0
=>7x=-35
=>x=-5
b: \(\dfrac{8-x}{x-7}-8=\dfrac{1}{x-7}\)
=>8-x-8(x-7)=1
=>8-x-8x+56=1
=>-9x+64=1
=>-9x=-63
hay x=7(loại)
a, \(7x=-35\Leftrightarrow x=-5\)
b, đk : x khác 7
\(8-x-8x+56=1\Leftrightarrow-9x=-63\Leftrightarrow x=7\left(ktm\right)\)
vậy pt vô nghiệm
2, thiếu đề
1.
\(a,7x+35=0\\ \Rightarrow7x=-35\\ \Rightarrow x=-5\\ b,ĐKXĐ:x\ne7\\ \dfrac{8-x}{x-7}-8=\dfrac{1}{x-7}\\ \Leftrightarrow\dfrac{8-x}{x-7}-\dfrac{8\left(x-7\right)}{x-7}-\dfrac{1}{x-7}=0\\ \Leftrightarrow\dfrac{8-x-8x+56-1}{x-7}=0\\ \Rightarrow-9x+63=0\\ \Leftrightarrow-9x=-63\\ \Leftrightarrow x=7\left(ktm\right)\)
2.đề thiếu
Giúp em giải phương trình 2(3x+1)+1/4-5=2(3x-1)/5-3x+2/10
Giải phương trình
a) 2(9x^2 + 6x + 1) = (3x+1)(x-2)
b) 12/1-9x^2 = 1-3x/1+3x - 1+3x/1-3x
a) \(2\left(9x^2+6x+1\right)=\left(3x+1\right)\left(x-2\right)\)
\(\Leftrightarrow\)\(2\left(3x+1\right)^2-\left(3x+1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\)\(\left(3x+1\right)\left[2\left(3x+1\right)-\left(x-2\right)\right]=0\)
\(\Leftrightarrow\)\(\left(3x+1\right)\left(6x+2-x+2\right)=0\)
\(\Leftrightarrow\)\(\left(3x+1\right)\left(5x+4\right)=0\)
đến đây tự lm nha
b) \(\frac{12}{1-9x^2}=\frac{1-3x}{1+3x}-\frac{1+3x}{1-3x}\) (1)
ĐKXĐ: \(x\ne\pm\frac{1}{3}\)
\(\left(1\right)\)\(\Leftrightarrow\)\(\frac{12}{\left(1-3x\right)\left(1+3x\right)}=\frac{\left(1-3x\right)^2}{\left(1+3x\right)\left(1-3x\right)}-\frac{\left(1+3x\right)^2}{\left(1-3x\right)\left(1+3x\right)}\)
\(\Rightarrow\)\(\left(1-3x\right)^2-\left(1+3x\right)^2=12\)
\(\Leftrightarrow\)\(\left(1-3x-1-3x\right)\left(1-3x+1+3x\right)=12\)
\(\Leftrightarrow\)\(-12x=12\)
\(\Leftrightarrow\)\(x=-1\) (t/m ĐKXĐ)
Vậy....
a) \(2\left(9x^2+6x+1\right)=\left(3x+1\right)\left(x-2\right)\)
\(\Leftrightarrow2\left(3x+1\right)^2-\left(3x+1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left(3x+1\right)\left[2\left(3x+1\right)-\left(x-2\right)\right]=0\)
\(\Leftrightarrow\left(3x+1\right)\left(6x+2-x+2\right)=0\)
\(\Leftrightarrow\left(3x+1\right)\left(5x+4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}3x+1=0\\5x+4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{-1}{3}\\x=-\frac{4}{5}\end{cases}}}\)
b) ĐKXĐ: \(x\ne\pm\frac{1}{3}\)
\(\frac{12}{1-9x^2}=\frac{1-3x}{1+3x}-\frac{1+3x}{1-3x}\)
\(\Leftrightarrow\frac{12}{\left(1-3x\right)\left(1+3x\right)}=\frac{\left(1-3x\right)^2}{\left(1-3x\right)\left(1+3x\right)}-\frac{\left(1+3x\right)^2}{\left(1-3x\right)\left(1+3x\right)}\)
\(\Leftrightarrow\left(1-3x\right)^2-\left(1+3x\right)^2=12\)
\(\Leftrightarrow\left(1-3x-1-3x\right)\left(1-3x+1+3x\right)=12\)
\(\Leftrightarrow-12x=12\)
\(\Leftrightarrow x=-1\) (thỏa mãn)
Vậy x = -1
Giải phương trình: (3x – 1)(x2 + 2) = (3x – 1)(7x – 10).
(3x – 1)(x2 + 2) = (3x – 1)(7x – 10)
⇔ (3x – 1)(x2 + 2) – (3x – 1)(7x – 10) = 0
⇔ (3x – 1)(x2 + 2 – 7x + 10) = 0
⇔ (3x – 1)(x2 – 7x + 12) = 0
⇔ (3x – 1)(x2 – 4x – 3x + 12) = 0
⇔ (3x – 1)[(x2 – 4x) – (3x - 12)] = 0
⇔ (3x – 1)[x(x – 4) – 3(x – 4)] = 0
⇔ (3x – 1)(x – 3)(x – 4) = 0
⇔ 3x – 1 = 0 hoặc x – 3 = 0 hoặc x – 4 = 0
+ 3x – 1 = 0 ⇔ 3x = 1 ⇔ x = 1/3.
+ x – 3 = 0 ⇔ x = 3.
+ x – 4 = 0 ⇔ x = 4.
Vậy phương trình có tập nghiệm là 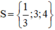
GIẢI PHƯƠNG TRÌNH
a,
b, (3x-1)(4x+3)=2(3x-1)
a) \(6x^2-5x+3=2x-3x\left(3-2x\right)\)
\(\Leftrightarrow6x^2-5x+3=2x-9x+6x^2\)
\(\Leftrightarrow2x=-3\Leftrightarrow x=-\dfrac{3}{2}\)
b) \(\left(3x-1\right)\left(4x+3\right)=2\left(3x-1\right)\)
\(\Leftrightarrow\left(3x-1\right)\left(4x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=-\dfrac{1}{4}\end{matrix}\right.\)
Giải các phương trình sau:
a,|-5x|+|7-x|=27
b,|3x-1|+|x+4|=21
c,2|3x|-5|x+2|=-7
d,|3x-5|+2=|15-3x|
e,|2x+1|-|5-3x|=2
giải phương trình (3x-2)((x+1)^2)(3x+8)= -16
=>(9x^2+24x-6x-16)(x^2+2x+1)=-16
=>(9x^2+18x-16)(x^2+2x+1)=-16
=>(9x^2+18x+9-25)(x^2+2x+1)=-16
=>[9(x+1)^2-25](x+1)^2=-16
=>9(x+1)^4-25(x+1)^2+16=0
Đặt (x+1)^2=a
=>9a^2-25a+16=0
=>a=1 hoặc a=16/9
=>(x+1)^2=1 hoặc (x+1)^2=16/9
=>\(x\in\left\{0;-2;\dfrac{1}{3};-\dfrac{7}{3}\right\}\)
giải phương trình;(3x-1)(x^2+2)=(3x-1)(7x-10)
\(\left(3x-1\right)\left(x^2+2\right)=\left(3x-1\right)\left(7x-10\right)\)
\(\Leftrightarrow\left(3x-1\right)\left(x^2+2\right)-\left(3x-1\right)\left(7x-10\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(x^2+2-7x+10\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(x^2-7x+12\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(x^2-4x-3x+12\right)=0\)
\(\Leftrightarrow\left(3x-1\right)[x\left(x-4\right)-3\left(x-4\right)]=0\)
\(\Leftrightarrow\left(3x-1\right)\left(x-4\right)\left(x-3\right)=0\)
Tương đương với 1 trong 3 biểu thức trên bằng 0.
Giải ra 3 nghiệm là \(x=\frac{1}{3};x=4;x=3\)
giải phương trình: √(3x^2+5x-8)-√(3x^2+5x+1)=1
Đặt\(3x^2+5x-8=a\)\(\Rightarrow3x^2+5x+1=a+9\), từ đó phương trình có dạng \(\sqrt{a}-\sqrt{a+9}=1\), bn giải phương trình bình thường tìm ra a, rồi suy ra x nha!. Học tốt
Giải phương trình:
(3x-1)2 -3(3x-2)=9(x+1)(x-3)
PT \(\Leftrightarrow9x^2-6x+1-9x+6=9x^2-18x-27\)
\(\Leftrightarrow9x^2-6x+1-9x+6-9x^2+18x+27=0\)
\(\Leftrightarrow3x+34=0\)
\(\Leftrightarrow x=-\dfrac{34}{3}\)
Vậy ...
Ta có: \(\left(3x-1\right)^2-3\left(3x-2\right)=9\left(x+1\right)\left(x-3\right)\)
\(\Leftrightarrow9x^2-6x+1-9x+6=9\left(x^2-3x+x-3\right)\)
\(\Leftrightarrow9x^2-15x+7=9x^2-18x-27\)
\(\Leftrightarrow9x^2-15x+7-9x^2+18x+27=0\)
\(\Leftrightarrow3x+34=0\)
\(\Leftrightarrow3x=-34\)
\(\Leftrightarrow x=-\dfrac{34}{3}\)
Vậy: \(S=\left\{-\dfrac{34}{3}\right\}\)