Bài 1. Trong mặt phẳng toạ độ Oxy cho tam giác ABC với A(-1;1); B(3;1);C(2;4)
a. Tính chu vi của tam giác ABC và tính góc giữa hai vectơ \(\overrightarrow{AB},\overrightarrow{CA}\)
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC với A(6;2), B(-4;-3) và C(0;5)
1, Chứng minh tam giác ABC vuông. Tính diện tích tam giác ABC
2, Tìm toạ độ giao điểm của đường tròn ngoại tiếp tam giác ABC và trục tung
3, Tìm toạ độ tâm đường tròn nội tiếp tam giác ABC
1: \(\overrightarrow{AB}=\left(-10;-5\right)\)
\(\overrightarrow{AC}=\left(-6;3\right)\)
\(\overrightarrow{BC}=\left(4;8\right)\)
Vì \(\overrightarrow{AC}\cdot\overrightarrow{BC}=0\) ΔABC vuông tại C
\(AC=\sqrt{\left(-6\right)^2+3^2}=3\sqrt{5}\)
\(BC=\sqrt{4^2+8^2}=4\sqrt{5}\)
Do đó: \(S_{ABC}=\dfrac{AC\cdot BC}{2}=\dfrac{3\sqrt{5}\cdot4\sqrt{5}}{2}=3\sqrt{5}\cdot2\sqrt{5}=30\)
Trong mặt phẳng với hệ toạ độ Oxy cho tam giác ABC. Hai điểm M 4 ; - 1 , N 0 ; - 5 lần lượt thuộc AB, AC và phương trình đường phân giác trong góc A là x - 3 y + 5 = 0 , trọng tâm của tam giác ABC là G. Tìm toạ độ các đỉnh của tam giác ABC
A. A 1 ; 2 , B - 2 ; 5 , C - 1 ; 12
B. A 1 ; 2 , B - 2 ; 5 , C 0 ; 1
C. A 1 ; 0 , B - 2 ; 5 , C - 1 ; 12
D. A 1 ; 2 , B - 1 ; 5 , C - 1 ; 12
Đáp án A
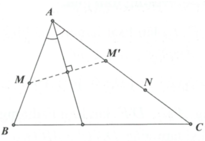
Phân tích.
- Ta thấy A thuộc đường phân giác trong góc A: x - 3 y + 5 = 0 giờ chỉ cần viết được phương trình AC là tìm được A.
- Trên AC đã có một điểm N, cần tìm thêm một điểm nữa. Chú ý khi lấy M’ đối xứng với M qua phân giác trong ta có M’ thuộc cạnh AC.
- Tìm M’ viết được phương trình AC từ đó suy ra A. Có A, M viết được phương trình AB.
- Gọi B, C và tham số hóa dựa vào B thuộc AB, C thuộc AC. Áp dụng công thức trọng tâm sẽ tìm ra được tọa độ B, C.
Hướng dẫn giải.
Gọi M ' ∈ A C là điểm đối xứng của M qua phân giác trong góc A, gọi I là giao điểm của MM' với phân giác trong góc A → I là trung điểm MM’.
Phương trình MM’ là: 3 x + y - 11 = 0
Toạ độ điểm I là nghiệm của hệ:
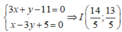
M’ đối xứng với M qua
![]()
Đường thẳng AC qua N và M’ nên có phương trình:
![]()
Tọa độ A là nghiệm của hệ:
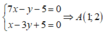
Đường thẳng AB đi qua A, M nên có phương trình:
x + y - 3 = 0
Gọi
![]()
Do G là trọng tâm tam giác ABC nên ta có:
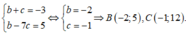
Vậy tọa độ các đỉnh của tam giác ABC là:
![]()
Trong mặt phẳng toạ độ Oxy cho tam giác ABC có A(1;1) , B(2;-1) , C(3;3) . Toạ độ điểm E để tứ giác ABCE là hình bình hành là
Gọi E(x;y) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(1;-2\right)\\\overrightarrow{EC}=\left(3-x;3-y\right)\end{matrix}\right.\)
Tứ giác ABCE là hbh khi \(\overrightarrow{AB}=\overrightarrow{EC}\)
\(\Leftrightarrow\left\{{}\begin{matrix}3-x=1\\3-y=-2\end{matrix}\right.\) \(\Rightarrow E\left(2;5\right)\)
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(6,0); B(3,1); C(-1,-1).Tính số đo góc B của tam giác đã cho
\(\left\{{}\begin{matrix}\overrightarrow{BA}=\left(3;-1\right)\\\overrightarrow{BC}=\left(-4;-2\right)\end{matrix}\right.\)
\(\Rightarrow cos\widehat{ABC}=cos\left(\overrightarrow{BA};\overrightarrow{BC}\right)=\dfrac{3.\left(-4\right)+1.2}{\sqrt{3^2+1^2}.\sqrt{\left(-4\right)^2+\left(-2\right)^2}}=-\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{ABC}=135^0\)
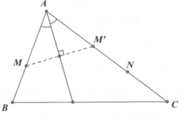
Trong mặt phẳng với hệ toạ độ Oxy cho tam giác ABC. Hai điểm M(4;-1),N(0;-5) lần lượt thuộc AB, AC và phương trình đường phân giác trong góc A là x- 3y+5 = 0, trọng tâm của tam giác ABC là G. Tìm toạ độ các đỉnh của tam giác ABC.
![]()
![]()
![]()
![]()
Chọn A
Phân tích.
- Ta thấy A thuộc đường phân giác trong góc A:x-3y+5=0 , giờ chỉ cần viết được phương trình AC là tìm được A.
- Trên AC đã có một điểm N, cần tìm thêm một điểm nữa. Chú ý khi lấy M’ đối xứng với M qua phân giác trong ta có M’ thuộc cạnh AC.
- Tìm M’ viết được phương trình AC từ đó suy ra A. Có A, M viết được phương trình AB.
- Gọi B, C và tham số hóa dựa vào B thuộc AB, C thuộc AC. Áp dụng công thức trọng tâm sẽ tìm ra được tọa độ B, C.



Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(-3,0); B(3,0); và C(2,6). Tìm toạ độ trục tâm H của tam giác ABC
Gọi \(H\left(x;y\right)\) là trực tâm tam giác
\(\Rightarrow\overrightarrow{AH}=\left(x+3;y\right)\) ; \(\overrightarrow{BH}=\left(x-3;y\right)\); \(\overrightarrow{BC}=\left(-1;6\right)\) ; \(\overrightarrow{AC}=\left(5;6\right)\)
Do H là trực tâm tam giác \(\Rightarrow\left\{{}\begin{matrix}AH\perp BC\\BH\perp AC\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{AC}=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-\left(x+3\right)+6y=0\\5\left(x-3\right)+6y=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-x+6y=3\\5x+6y=15\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{5}{6}\\\end{matrix}\right.\) \(\Rightarrow H\left(2;\dfrac{5}{6}\right)\)
Giúp em với ạ em cảm ơn!
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(6;-1) B(-1;2) C(2;5)
a) tính độ dài 3 cạnh vf số đo 3 góc của tam giác ABC
b)Tính chu vi và diện tích của tam giác ABC
c) Tìm toạ độ trực tâm , trọng tâm tam giác ABC.
Gợi ý thôi nhé.
a) Có \(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}=\sqrt{\left(\left(-1\right)-6\right)^2+\left(2-\left(-1\right)\right)^2}=\sqrt{58}\)
Tương tự như vậy, ta tính được AC, BC.
Tính góc: Dùng \(\cos A=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}\)
b) Chu vi thì bạn lấy 3 cạnh cộng lại.
Diện tích: Dùng \(S_{ABC}=\dfrac{1}{2}AB.AC.\sin A\)
c) Gọi \(H\left(x_H,y_H\right)\) là trực tâm thì \(\left\{{}\begin{matrix}AH\perp BC\\BH\perp AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{AC}=0\end{matrix}\right.\)
Sau đó dùng: \(\overrightarrow{u}\left(x_1,y_1\right);\overrightarrow{v}\left(x_2,y_2\right)\) thì \(\overrightarrow{u}.\overrightarrow{v}=x_1x_2+y_1y_2\) để lập hệ phương trình tìm \(x_H,y_H\)
Trọng tâm: Gọi \(G\left(x_G,y_G\right)\) là trọng tâm và M là trung điểm BC. Dùng \(\left\{{}\begin{matrix}x_M=\dfrac{x_B+x_C}{2}\\y_M=\dfrac{y_B+y_C}{2}\end{matrix}\right.\) để tìm tọa độ M.
Dùng \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\) để lập hpt tìm tọa độ G.
Trong mặt phẳng toạ độ Oxy, cho 2 điểm A(1,2) và B(-3,1). Tìm toạ độ điểm C thuộc trục tung sao cho tam giác ABC vuông tại A. Tính diện tích tam giác ABC
Do C thuộc trục tung nên tọa độ có dạng \(C\left(0;c\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-4;-1\right)\\\overrightarrow{AC}=\left(-1;c-2\right)\end{matrix}\right.\)
Do tam giác ABC vuông tại A \(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=0\)
\(\Rightarrow4-\left(c-2\right)=0\Rightarrow c=6\)
\(\Rightarrow C\left(0;6\right)\)
\(\Rightarrow\overrightarrow{AC}=\left(-1;4\right)\Rightarrow\left\{{}\begin{matrix}AB=\sqrt{\left(-4\right)^2+\left(-1\right)^2}=\sqrt{17}\\AC=\sqrt{\left(-1\right)^2+4^2}=\sqrt{17}\end{matrix}\right.\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{17}{2}\)
Trong mặt phẳng toạ độ Oxy cho tam giác ABC nội tiếp đường tròn tâm I và D là chân đường phân giác trong đỉnh A của tam giác ABC biết toạ độ các đieemr A(2;6) I(-1/2;1) D(2;-3/2) biết phương trình tổng quát của đường thẳng BC
Trong mặt phẳng toạ độ oxy cho A(-1;-2)B(3;2)C(4;1) A gpij I là trung điểm của AB tìm toạ độ của I B gọi G là trọng tâm của tam giác ABC tìm toạ độ trọng tâm
a) Ta có: I là trung điểm AB
\(\Rightarrow\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=\dfrac{-1+3}{2}=1\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{-2+2}{2}=0\end{matrix}\right.\)
\(\Rightarrow I\left(1;0\right)\)
b) Ta có: G là trọng tâm tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}x_G=\dfrac{x_A+x_B+x_C}{3}=\dfrac{-1+3+4}{3}=2\\y_G=\dfrac{y_A+y_B+y_C}{3}=\dfrac{-2+2+1}{3}=\dfrac{1}{3}\end{matrix}\right.\)
\(\Rightarrow G\left(2;\dfrac{1}{3}\right)\)