B9 Tam giác ABC có \(BC=5\sqrt{5}\) ,\(AC=5\sqrt{2}\) AB=5 Tính \(\widehat{A}\)
cho tam giác ABC có BC=2, hc=\(\sqrt{2}\), R = \(\sqrt{5}\). Tính AB, AC
tam giác ABC có BC=\(\sqrt{5}\), AC=3 và cotC=2. tính cạnh AB.
cot C=2
=>\(tanC=\dfrac{1}{cotC}=\dfrac{1}{2}\)
\(1+tan^2C=\dfrac{1}{cos^2C}\)
=>\(cos^2C=1+\dfrac{1}{4}=\dfrac{5}{4}\)
=>\(cosC=\dfrac{2}{\sqrt{5}}\) hoặc \(cosC=-\dfrac{2}{\sqrt{5}}\)
TH1: \(cosC=\dfrac{2}{\sqrt{5}}\)
=>\(\dfrac{BC^2+AC^2-AB^2}{2\cdot BC\cdot AB}=\dfrac{2}{\sqrt{5}}\)
=>\(\dfrac{5+9-AB^2}{6\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)
=>\(14-AB^2=12\)
=>AB^2=2
=>\(AB=\sqrt{2}\)
TH2: \(cosC=-\dfrac{2}{\sqrt{5}}\)
=>\(\dfrac{5+9-AB^2}{6\sqrt{5}}=-\dfrac{2}{\sqrt{5}}\)
=>\(14-AB^2=\dfrac{-2}{\sqrt{5}}\cdot6\sqrt{5}=-12\)
=>AB^2=26
=>\(AB=\sqrt{26}\)
Tam giác ABC có: AB=\(a\sqrt{5}\);BC=\(a\sqrt{3}\);AC=\(a\sqrt{2}\)
a) Chứng minh tam giác ABC vuông
b) Tính các tỉ số lượng giác của \(\widehat{B}\).Từ đó suy ra các tỉ số lượng giác của \(\widehat{A}\)
Mọi người giải giúp mik vs mik đang cần gấp.Thanks mọi người nhìu <3
a. Ta thấy \(\left(a\sqrt{5}\right)^2=\left(a\sqrt{3}\right)^2+\left(a\sqrt{2}\right)^2\Rightarrow AB^2=BC^2+AC^2\)
\(\Rightarrow\Delta ABC\)vuông tại C
b. \(\sin B=\frac{AC}{AB}=\frac{\sqrt{2}}{\sqrt{5}}=\frac{\sqrt{10}}{5};\cos B=\frac{CB}{AB}=\frac{\sqrt{3}}{\sqrt{5}}=\frac{\sqrt{15}}{5}\)
\(\tan B=\frac{AC}{AB}=\frac{\sqrt{6}}{3};\cot B=\frac{\sqrt{6}}{2}\)
\(\sin A=\cos B=\frac{\sqrt{15}}{5};\cos A=\sin B=\frac{\sqrt{10}}{5}\)
\(\tan A=\cot B=\frac{\sqrt{6}}{2};\cot A=\tan B=\frac{\sqrt{6}}{3}\)
Cho tam giác ABC vuông tại A có\(\widehat{B}\)= 2.\(\widehat{C}\)
a) Tính \(\widehat{B}\)và \(\widehat{C}\)
b) Biết BC = 5cm; AC = \(\frac{5\sqrt{3}}{2}\). Tính AB
Cho tam giác ABC vuông tại A tính BH,CH, AC ,AH biết:
1, AB =12 cm BC= 13cm
AB =5 cm BC= 1dm
AB =3\(\sqrt{3}\) cm BC= 9cm
2,Tính BC ,AH, BH ,CH
AB =24 cm AC= 18cm
AB =2\(\sqrt{2}\) cm AC= 2\(\sqrt{2}\)cm
AB =3\(\sqrt{3}\) cm AC= 9cm
Cho tam giác ABC; biết AB = 6a,AC = 8a, BC \(4\sqrt{5}a\) . Tính \(\overrightarrow{AB}.\overrightarrow{AC}\) . theo a
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=\dfrac{5}{24}\)
\(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.cosA=10a^2\)
Cho tam giác ABC vuông tại A có I là giao điểm 3 đường phân giác của tam giác ABC.
a) Trong đó AB = 5 cm IC =6 cm.Tính BC
b)IB =\(\sqrt{5}\) IC =\(\sqrt{10}\) Tính AB, AC
Cho tam giác ABC có \(\widehat{C}\)= 30o và BC=\(\sqrt{3}\);AC=2.Tính cạnh AB bằng?
Cho tam giác ABC có \(AB = 5,BC = 7,\widehat A = {120^o}.\) Tính độ dài cạnh AC.
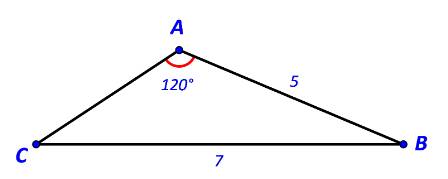
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow \sin C = \sin A.\frac{{AB}}{{BC}} = \sin {120^o}.\frac{5}{7} = \frac{{5\sqrt 3 }}{{14}}\)
\( \Rightarrow \widehat C \approx 38,{2^o}\) hoặc \(\widehat C \approx 141,{8^o}\) (Loại)
Ta có: \(\widehat A = {120^o},\widehat C = 38,{2^o}\)\( \Rightarrow \widehat B = {180^o} - \left( {{{120}^o} + 38,{2^o}} \right) = 21,{8^o}\)
Áp dụng định lí cosin trong tam giác ABC ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {5^2} + {7^2} - 2.5.7.\cos 21,{8^o}\\ \Rightarrow A{C^2} \approx 9\\ \Rightarrow AC = 3\end{array}\)
Vậy độ dài cạnh AC là 3.