Cho tam giác IAB có IA =IB M là trung điểm AB
a) IM là tia phân giác của góc AIB
help vs
Những câu hỏi liên quan
Cho tam giác IAB có IA =IB M là trung điểm AB
a) IM vuông góc với AB giúp
=) giúp nốt ik
a: Ta có: ΔIAB cân tại I
mà IM là đường trung tuyến ứng với cạnh đáy AB
nên IM là đường cao ứng với cạnh AB
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, M là trung điểm của Bc. Tia phân giác của góc ABC cắt AC tại I. Biết BI vuông góc với AM tại H.
a) Chứng minh IA = IM
b) Trên tia đối của tia HB lấy điểm K sao cho HK = HB. Chứng minh tam giác AIB = tam giác KIC
cho tam giác abc có góc a bằng 90 độ i là trung điểm của bc trên tia đối của tia ia lấy điểm k sao cho ia bằng ik CMR
a, tam giác iab bằng tam giác ikc
b, kc vuông góc với ac
c,bk song song vs ac
a: Xét ΔIAB và ΔIKC có
IA=IK
góc AIB=góc KIC
IB=IC
=>ΔIAB=ΔIKC
b: ΔIAB=ΔIKC
=>góc IAB=góc IKC
=>AB//KC
=>KC vuông góc AC
c: Xét tứ giác ABKC có
I là trung điểm chung của AK và BC
=>ABKC là hfinh bình hành
=>BK//AC
Đúng 0
Bình luận (0)
Cho tam giác ABC ( AB< AC ) Trên tia CA lấy điểm D sao cho CD= AB . Các đường trung trực của doạn thẳng BC và AC cắt nhau tại I
a) IA = ID; IB=IC
b) Tam giác IAB = TAM GIÁC IDC
c) AI là phân giác của góc BAC
a: Sửa đề; IA=IC
Ta có: I nằm trên đường trung trực của AC
nên IA=IC
Ta có: I nằm trên đường trung trực của BC
nên IB=IC
b: Xét ΔIAB và ΔIDC có
IA=ID
IB=IC
AB=DC
Do đó: ΔIAB=ΔIDC
Đúng 2
Bình luận (0)
a: Sửa đề; IA=IC
Ta có: I nằm trên đường trung trực của AC
nên IA=IC
Ta có: I nằm trên đường trung trực của BC
nên IB=IC
b: Xét ΔIAB và ΔIDC có
IA=ID
IB=IC
AB=DC
Do đó: ΔIAB=ΔIDC
Đúng 0
Bình luận (1)
cho tam giác ABC, góc A>90 độ. I là trung điểm AC. Trên tia đối tia IB lấy D sao IB=ID
a) CM tam giác AIB= tam giác CID
b) CM AD=BC
c) Gọi M là trung điểm BC , N là trung đểm AD.
CM IM=IN
d) CM I là trung điểm MN
e) CM góc AIB < góc BIC
a: Xet ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
=>ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
=>ABCD là hình bình hành
=>AD=BC và AD//CB
c,d: Xét tứ giác ANCM có
AN//CM
AN=CM
=>ANCM là hìnhbình hành
=>AC cắt NM tại trung điểm của mỗi đường
=>I là trung điểm của MN
=>IM=IN
Đúng 0
Bình luận (0)
Cho tam giác ABC có số đo góc A=90 độ, gọi I là trung điểm của BC. Trên tia đối của tia IA lấy điểm M sao cho IM=IA
a) Chứng minh tam giác AIB = tam giác MIC
b) Chứng minh AB // CM
c) Chứng minh AI = 1/2 BC
4)cho tam giác ABC ( AB AC ). Trên tia đối của tia CA lấy điểm D sao cho CDAB. Các đường trung trực của các đoạn thẳng BC và AD cắt nhau tại I. chứng minh rằng: a) IAID;IBIC b) tam giác IAB tam giác IDC c)AI là tia phân giác cảu góc BAC5)cho tỉ lệ thức: dfrac{a}{b}dfrac{c}{d}. chứng minh rằng ta có tỉ lệ thức sau : left(dfrac{a+b}{c+d^{ }}right)^2 dfrac{a^2+b^2}{c^2+d^2}
Đọc tiếp
4)cho tam giác ABC ( AB <AC ). Trên tia đối của tia CA lấy điểm D sao cho CD=AB. Các đường trung trực của các đoạn thẳng BC và AD cắt nhau tại I. chứng minh rằng:
a) IA=ID;IB=IC
b) tam giác IAB= tam giác IDC
c)AI là tia phân giác cảu góc BAC
5)cho tỉ lệ thức: \(\dfrac{a}{b}=\dfrac{c}{d}\). chứng minh rằng ta có tỉ lệ thức sau : \(\left(\dfrac{a+b}{c+d^{ }}\right)^2\)= \(\dfrac{a^2+b^2}{c^2+d^2}\)
5. ta có:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\) \(a.b=c.d\)
\(\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{\left(a+b\right)^2-2ab}{\left(c+d\right)^2-2cd}\)
Mà a+b = c+ d; ab = cd
=> đfcm
Đúng 1
Bình luận (0)
Bài 4:
a: Ta có: I nằm trên đường trung trực của AD
nên IA=ID
Ta có: I nằm trên đường trung trực của BC
nên IB=IC
b: Xét ΔIAB và ΔIDC có
IA=ID
\(\widehat{AIB}=\widehat{DIC}\)
IB=IC
Do đó: ΔIAB=ΔIDC
Đúng 0
Bình luận (0)
Câu 5:
Đặt $\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk; c=dk$
Khi đó:
$(\frac{a+b}{c+d})^2=(\frac{bk+b}{dk+d})^2=[\frac{b(k+1)}{d(k+1)}]^2=\frac{b^2}{d^2}(1)$
$\frac{a^2+b^2}{c^2+d^2}=\frac{(bk)^2+b^2}{(dk)^2+d^2}=\frac{b^2(k^2+1)}{d^2(k^2+1)}=\frac{b^2}{d^2}(2)$
Từ $(1); (2)\Rightarrow (\frac{a+b}{c+d})^2=\frac{a^2+b^2}{c^2+d^2}$ (đpcm)
Đúng 0
Bình luận (0)
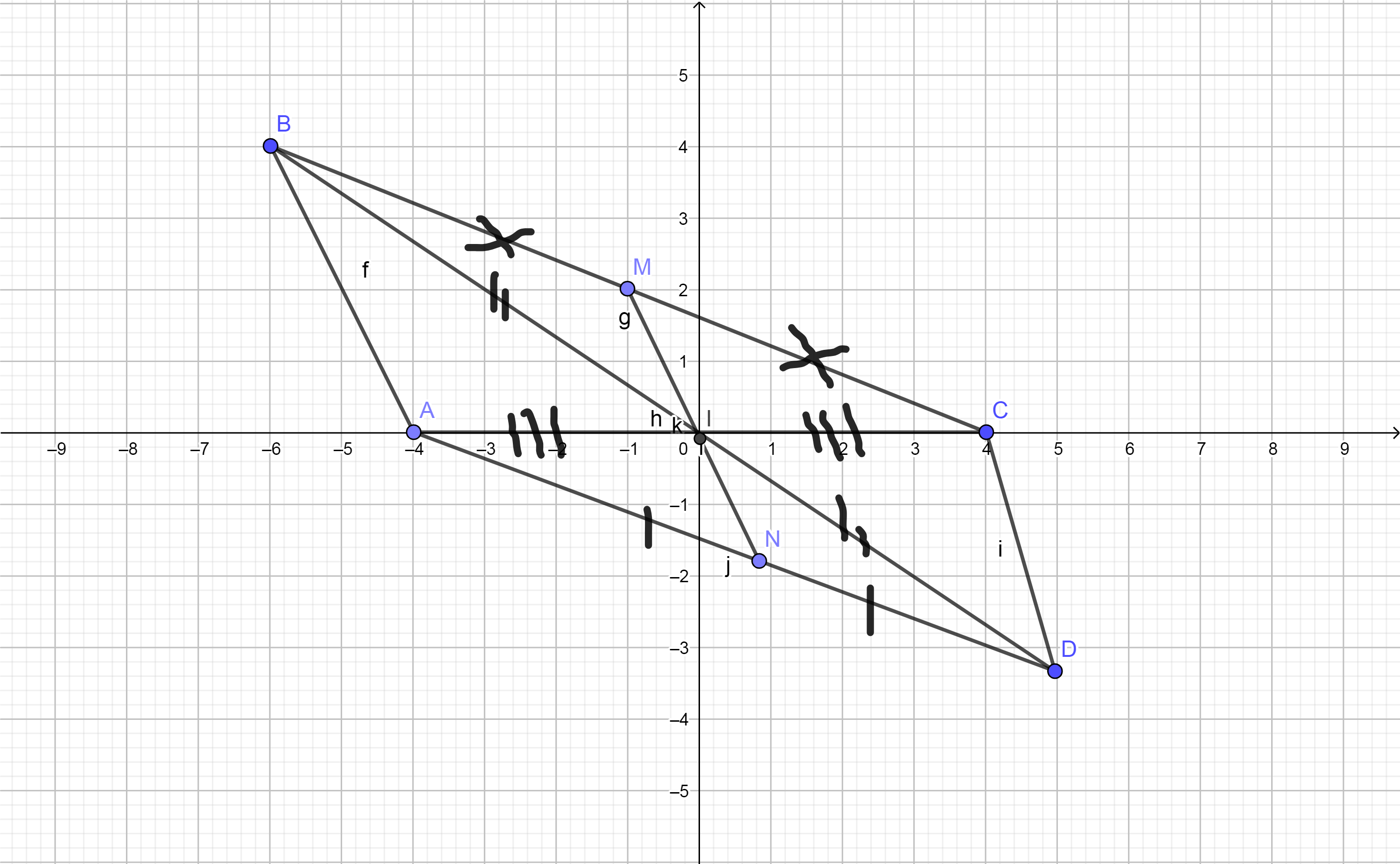
Cho tam giác ABC có góc A>90 độ. Gọi I là trung điểm AC, trên tia đối của tia IB lấy điểm D sao cho IB=ID. Nối C vs D. Chứng minh
a, Tam giác AIB= tam giác CID
b, Gọi M là trung điểm BC, N là trung điểm AD chứng minh I là trung điểm MN
c, Chứng minh góc AlB< góc BlC
Cho tam giác ABC có góc A lớn hơn 90độ. Gọi I là trung điểm của cạnh AC. Trên tia đối của tia IB lấy điểm D sao cho IBIDa/CM: tam giác AIBtám giác CIDb/CM:ADBCc/Gọi M trung điểm của BC, N trung điểm của AD. CM: I trung điểm của MNd/CM: Góc AIB bé hơn góc BICe/Tìm điều kiện tam giác ABC để AC vuông góc CDPS:làm nhanh giúp mình với mình cần rất rất gấp
Đọc tiếp
Cho tam giác ABC có góc A lớn hơn 90độ. Gọi I là trung điểm của cạnh AC. Trên tia đối của tia IB lấy điểm D sao cho IB=ID
a/CM: tam giác AIB=tám giác CID
b/CM:AD=BC
c/Gọi M trung điểm của BC, N trung điểm của AD.
CM: I trung điểm của MN
d/CM: Góc AIB bé hơn góc BIC
e/Tìm điều kiện tam giác ABC để AC vuông góc CD
PS:làm nhanh giúp mình với mình cần rất rất gấp
a.Xét tam giác AIBAIB và tam giác CIDCID có:
IA=ICIA=IC ( gt )
Góc CIDCID = Góc AIBAIB (ĐỐI ĐỈNH)
ID=IBID=IB ( gt )
⇒Tam giác AIBAIB = Tam giác CIDCID
b.Ta có Tam giác ABIABI = tam giác CDICDI
nên khoảng cách trung tuyến của MIMI và NINI đều bằng nhau.
⇒ II là trung điểm của đoạn MN.MN.
c.Xét góc AIBAIB và góc BICBIC ta có:
IA<ICIA<IC ( gt )
Góc BICBIC > Góc AIBAIB
IC>IBIC>IB ( gt )
⇒Góc AIBAIB < góc BICBIC
d.Điều kiện : Góc AA = 90o
Đúng 0
Bình luận (1)
a, Xét tam giác AIB và tam giác CID có:
AI=CI (gt)
BI=DI(gt)
gócBIA=gócCID (đối đỉnh)
=>tam giác AIB=tam giác CID(c.g.c)
b, Xét tam giác BIC và tam giác DIA có:
BI=DI(gt)
AI=IC(gt)
góc BIC=gócDIA(đối đỉnh)
=>tam giác BIC= tam giác DIA(c.g.c)
=>AD=BC(2 cạnh tương ứng)
c, Do tam giác BIC=tam giác DIA( câu b)
=> góc BCI=góc DAI (2 góc tương ứng)
Do BC=AD(câu b)
=> MC=AN ( đều là trung điểm của BC và AN)
Xét tam giác AIN và tam giác CIM có:
AI=IC (gt)
AN=MC(cm trên)
góc DAI=góc BCI (cm trên)
=>tam giác AIN=tam giác CIM(c.g.c)
=>IM=IN ( 2 cạnh tương ứng)
=> góc AIN= góc CIM ( 2 góc tương ứng)
Mà góc ÂIN+ góc NIC=180 độ ( 2 góc kề bù)
Do 3 điểm A,I,c thẳng hàng
=> góc CIM+NIC=180 độ ( vì góc AIN=CIM)
=> 3 điểm M,I,N thẳng hàng(1)
MI=NI ( câu c) (2)
từ (1) và (2) suy ra I là trung điểm của MN
d, Xét tam giác AIB có BIC là góc ngoài của tam giác AIB
=> góc BIC >Â>90 độ
=> góc BIC>90 độ
=> góc BIC > góc AIB
hay góc AIB<BIC
e,Xét tam giác ABI và tam giác CDI có:
AI=CI (gt)
góc BIA= góc CID (đối đỉnh)
BI=DI ( gt)
=> góc BAI=DCI ( 2 góc tương ứng)
nên để AC vuông góc CD hay DCI=90 độ thì BAI=90 độ
hay tam giác AIB vuông ở A.
Đúng 0
Bình luận (0)
🙄😀😁😂🤣😃😄😅😆