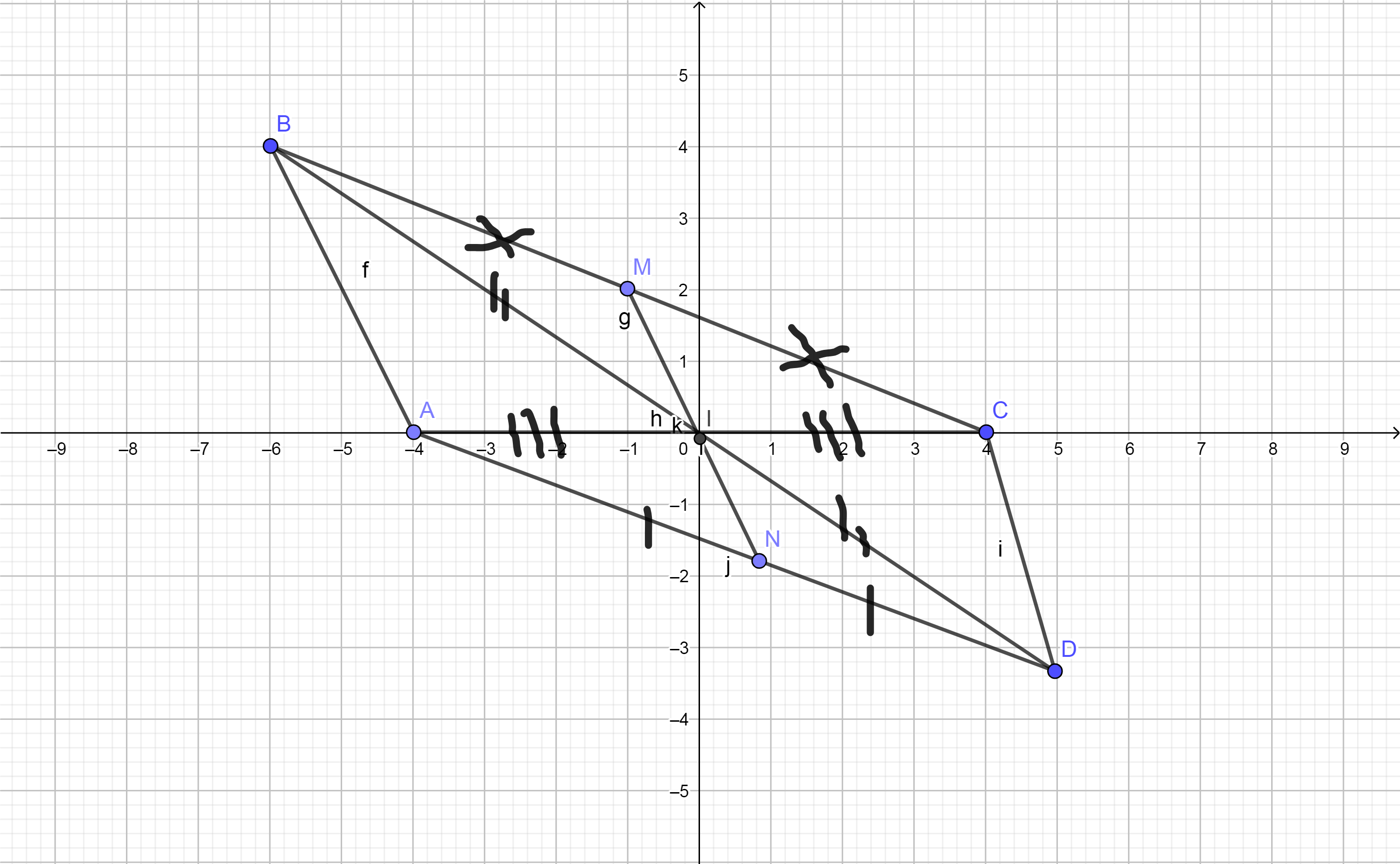
a, Xét tam giác AIB và tam giác CID có:
AI=CI (gt)
BI=DI(gt)
gócBIA=gócCID (đối đỉnh)
=>tam giác AIB=tam giác CID(c.g.c)
b, Xét tam giác BIC và tam giác DIA có:
BI=DI(gt)
AI=IC(gt)
góc BIC=gócDIA(đối đỉnh)
=>tam giác BIC= tam giác DIA(c.g.c)
=>AD=BC(2 cạnh tương ứng)
c, Do tam giác BIC=tam giác DIA( câu b)
=> góc BCI=góc DAI (2 góc tương ứng)
Do BC=AD(câu b)
=> MC=AN ( đều là trung điểm của BC và AN)
Xét tam giác AIN và tam giác CIM có:
AI=IC (gt)
AN=MC(cm trên)
góc DAI=góc BCI (cm trên)
=>tam giác AIN=tam giác CIM(c.g.c)
=>IM=IN ( 2 cạnh tương ứng)
=> góc AIN= góc CIM ( 2 góc tương ứng)
Mà góc ÂIN+ góc NIC=180 độ ( 2 góc kề bù)
Do 3 điểm A,I,c thẳng hàng
=> góc CIM+NIC=180 độ ( vì góc AIN=CIM)
=> 3 điểm M,I,N thẳng hàng(1)
MI=NI ( câu c) (2)
từ (1) và (2) suy ra I là trung điểm của MN
d, Xét tam giác AIB có BIC là góc ngoài của tam giác AIB
=> góc BIC >Â>90 độ
=> góc BIC>90 độ
=> góc BIC > góc AIB
hay góc AIB<BIC
e,Xét tam giác ABI và tam giác CDI có:
AI=CI (gt)
góc BIA= góc CID (đối đỉnh)
BI=DI ( gt)
=> góc BAI=DCI ( 2 góc tương ứng)
nên để AC vuông góc CD hay DCI=90 độ thì BAI=90 độ
hay tam giác AIB vuông ở A.