xét tam giác OAM và tam giác OBM có

OA  = OB

OM chung 

OAM= BOM

=> 2 tam giác = nhau

=> AM = MB

b, tam giác AOB coa AO = OB=> tam giác AOB cân tại 0 

=> Om là phân giác đồng thời là đường cao

=> OM vuông gó vs AB

cái câu a là cánh góc cạnh phải ko bạn

đúng rồi đó !

ccau a la canh gac canh !

Vì thế ....

tk tớ nha

1/

Xét tam giác OAM và tam giác OBM,ta có:

Cạnh OM là cạnh chung

OA = OB (gt)

góc AOM = góc BOM ( vì Ot là tia phân giác của góc xOy)

=> Tam giác OAM = tam giác OBM (c.g.c)

=> MA = MB ( 2 cạnh tương ứng)

2/

Ta có: MA = MB (cmt)

=> Tam giác AMB là tam giác cân

=> Góc MAH = góc MBH

Xét tam giác AMH và tam giác BMH,ta có:

góc MAH = góc MBH ( cmt)

MA = MB ( cmt)

góc AMH = góc BMH ( vì tam giác OAM = tam giác OBM)

=> tam giác AMH và tam giác BMH ( g.c.g)

=> AH = HB ( 2 cạnh tương ứng)

=> H là trung điểm của AB (1)

Vì tam giác AMH = tam giác BMH (cmt)

=>góc MHA = góc MHB ( 2 góc tương ứng)

mà góc MHA + góc MHB = 180 độ ( 2 góc kề bù)

=> góc MHA = góc MHB= 180 độ : 2 = 90 độ

=> MH vuông góc với AB (2)

Từ (1) và (2) => MH là đường trung trực của AB

=> OM là đường trung trực của AB ( vì H thuộc OM )

3/

Vì H là trung điểm của AB (cmt)

=> AH =HB = AB : 2 = 6 :2 = 3 (cm)

Xét tam giác OAH vuông tại H

Ta có: OA² = OH² + AH² ( định lí Py-ta-go)

=> 5² = OH² + 3²

=> 25 = OH² + 9

=> OH² = 25 - 9

=> OH² = 16 

=> OH = \(\sqrt{16}\)

=> OH = 4 cm

bạn làm đúng rồi đó mk xin tặng bạn 1 tk

oh=4cm

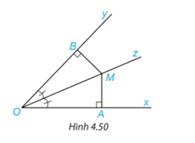
Xét hai tam giác vuông OBM và OAM có:

OM chung

\(\widehat {BOM} = \widehat {AOM}\) (gt)

\( \Rightarrow \Delta OBM = \Delta OAM\)(cạnh huyền – góc nhọn)

Suy ra MB=MA ( 2 cạnh tương ứng)

a:Xét ΔOAM và ΔOBM có 

OA=OB

\(\widehat{AOM}=\widehat{BOM}\)

OM chung

Do đó: ΔOAM=ΔOBM

Suy ra: MA=MB

b: Ta có: OA=OB

nên O nằm trên đường trung trực của AB(1)

Ta có: MA=MB

nên M nằm trên đường trung trực của AB(2)

Từ (1) và (2) suy ra MO là đường trung trực của AB

hay MO\(\perp\)AB