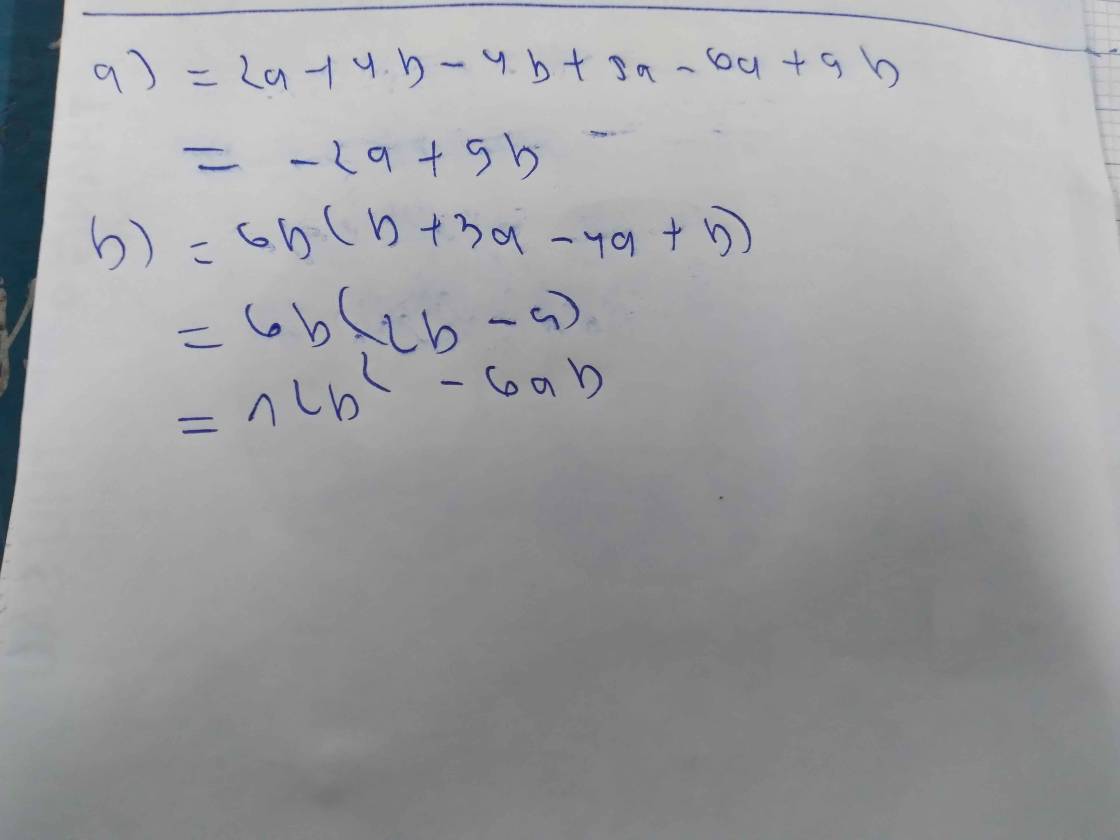Cho a2+ b2 +9= 6a+4b. Tìm Min, Max của S= 3a+4b
Những câu hỏi liên quan
Cho a2+b2+9=6a+4b. tìm max và min của E=3a+4b
Cho \(a^2+b^2+9=6a+4b\) Tìm Min, Max của \(Q=3a +4b\)
cho a,b,c >=0 thảo mãn 2a+b=6-3c và 3a+4b=3c+4
tìm MIN và MAX của B = 2a+3b-4c
24 tháng 12 2021 lúc 9:14
Câu 4: Giả sử cần tìm giá trị lớn nhất trong các ô A2, B2 và C2. Hàm nào sau đây là đúng?
A. max(A2,B2,C2) B. =max(A2,B2,C2) C. min(A2,B2,C2) D. =min(A2,B2,C2)
Xem thêm câu trả lời
Cho ba số thực dương a,b,c thỏa mãn
a
2
+
b
2
+
c
2
-
2
a
+
4
b
-
6
c
10
và a + c2 . Tính giá trị biểu thức P 3a + 2b + c khi
Q
a
2
+
b...
Đọc tiếp
Cho ba số thực dương a,b,c thỏa mãn a 2 + b 2 + c 2 - 2 a + 4 b - 6 c = 10 và a + c=2 . Tính giá trị biểu thức P = 3a + 2b + c khi Q = a 2 + b 2 + c 2 - 14 a - 8 b + 18 c đạt giá trị lớn nhất.
A. 10
B. -10
C. 12
D. -12
Đáp án D
Bài toán trở thành: Tìm M nằm trên đường tròn giao tuyến của mặt cầu (S) và mặt phẳng (P) sao cho KM lớn nhất
Đúng 0
Bình luận (0)
21 tháng 10 2021 lúc 14:01
Cho ab + bc + ac = 9 , a≥1 , b≥1 , c≥1
tìm min và max của bt P = a2+b2+c2
tìm a,b,c biết 4a-b2=4b-c2=4c-a2=1
Hai số tự nhiên a và b khi chia cho 2 dư lần lượt là 7 và 4.Tìm số dư khi chia cho 9 của 2a,3a,a+b,a.b,6a+5b,a2+b2.
Bài 2: tính
a) 2a + 4b + ( -4b + 5a) - (6a - 9b)
b) 6a [b + 3a - ( 4a - b )]
\(a.2a+4b+\left(-4b+5a\right)-\left(6a-9b\right)\)
\(=2a+4b-4b+5a-6a+9b\)
\(=\left(2a+5a-6a\right)+\left(4b-4b+9b\right)\)
\(=a+9b\)
\(b.6a\left[b+3a-\left(4a-b\right)\right]\)
\(=6a\left[b+3a-4a+b\right]\)
\(=6a\left[4a-a+b+b\right]\)
\(=6a\left(3a-2b\right)\)
Đúng 0
Bình luận (0)