a: Xét (O) có 

MA là tiếp tuyến có A là tiếp điểm

MB là tiếp tuyến có B là tiếp điểm

Do đó: MA=MB

Xét ΔMAB có MA=MB

nên ΔMAB cân tại M

Suy ra: \(\widehat{MAB}=\widehat{MBA}\)

Xét ΔDAB vuông tại D và ΔEBA vuông tại E có 

BA chung

\(\widehat{DBA}=\widehat{EAB}\)

Do đó: ΔDAB=ΔEBA

Suy ra: \(\widehat{DAB}=\widehat{EBA}\)

hay \(\widehat{HAB}=\widehat{HBA}\)

Xét ΔHBA có \(\widehat{HAB}=\widehat{HBA}\)

nên ΔHBA cân tại H

Suy ra: HA=HB

hay H nằm trên đường trung trực của AB(1)

Ta có:MA=MB

nên M nằm trên đường trung trực của AB(2)

Ta có: OA=OB

nên O nằm trên đường trung trực của AB(3)

Từ (1), (2) và (3) suy ra O,H,M thẳng hàng

a, Chú ý:  A M O ^ = A I O ^ = A N O ^ = 90 0

b,  A M B ^ = M C B ^ = 1 2 s đ M B ⏜

=> DAMB ~ DACM (g.g)

=> Đpcm

c, AMIN nội tiếp => A M N ^ = A I N ^

BE//AM => A M N ^ = B E N ^

=>   B E N ^ = A I N ^ => Tứ giác BEIN nội tiếp =>  B I E ^ = B N M ^

Chứng minh được:  B I E ^ = B C M ^ => IE//CM

d, G là trọng tâm DMBC Þ G Î MI

Gọi K là trung điểm AO Þ MK = IK = 1 2 AO

Từ G kẻ GG'//IK (G' Î MK)

=>  G G ' I K = M G M I = M G ' M K = 2 3 I K = 1 3 A O  không đổi   (1)

MG' =  2 3 MK => G' cố định (2). Từ (1) và (2) có G thuộc (G'; 1 3 AO)

Diện tích toàn phần của khối nhựa hình lập phương là:

10 x 10 x 6 = 600 (cm²)

Cạnh khối gỗ hình lập phương là:

10 : 2 = 5 (cm)

Diện tích toàn phần của khối gỗ hình lập phương là:

5 x 5 x 6 = 150 (cm²)

Diện tích toàn phần của khối nhựa gấp diện tích toàn phần của khối gấp số lần là:

600 : 150 = 4 (lần)

help me 

Tham khảo:

a) Ta có: \(\overrightarrow {MA}  + \overrightarrow {MB}  + 2\overrightarrow {MC}  = \overrightarrow 0  \Leftrightarrow \overrightarrow {MA}  + \left( {\overrightarrow {MA}  + \overrightarrow {AB} } \right) + 2\left( {\overrightarrow {MA}  + \overrightarrow {AC} } \right) = \overrightarrow 0 \)

\(\begin{array}{l} \Leftrightarrow 4\overrightarrow {MA}  + \overrightarrow {AB}  + 2\overrightarrow {AC}  = \overrightarrow 0 \\ \Leftrightarrow 4\overrightarrow {AM}  = \overrightarrow {AB}  + 2\overrightarrow {AC} \\ \Leftrightarrow \overrightarrow {AM}  = \frac{1}{4}\overrightarrow {AB}  + \frac{1}{2}\overrightarrow {AC} \end{array}\)

Trên cạnh AB, AC lấy điểm D, E sao cho \(AD = \frac{1}{4}AB;\;\,AE = \frac{1}{2}AC\)

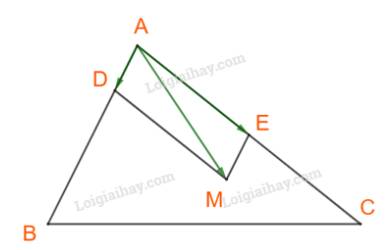
Khi đó \(\overrightarrow {AM}  = \overrightarrow {AD}  + \overrightarrow {AE} \) hay M là đỉnh thứ tư của hình bình hành AEMD.

b) Chứng minh rằng với mọi điểm O, ta có \(\overrightarrow {OA}  + \overrightarrow {OB}  + 2\overrightarrow {OC}  = 4\overrightarrow {OM} \)

Với mọi điểm O, ta có: \(\left\{ \begin{array}{l}\overrightarrow {OA}  = \overrightarrow {OM}  + \overrightarrow {MA} ;\;\\\overrightarrow {OB}  = \overrightarrow {OM}  + \overrightarrow {MB} ;\;\,\\\overrightarrow {OC}  = \overrightarrow {OM}  + \overrightarrow {MC} \end{array} \right.\)

\(\begin{array}{l} \Rightarrow \overrightarrow {OA}  + \overrightarrow {OB}  + 2\overrightarrow {OC}  = \left( {\overrightarrow {OM}  + \overrightarrow {MA} } \right) + \left( {\overrightarrow {OM}  + \overrightarrow {MB} } \right) + 2\left( {\overrightarrow {OM}  + \overrightarrow {MC} } \right)\\ = 4\overrightarrow {OM}  + \left( {\overrightarrow {MA}  + \overrightarrow {MB}  + 2\overrightarrow {MC} } \right) = 4\overrightarrow {OM}  + \overrightarrow 0  = 4\overrightarrow {OM} .\end{array}\)

Vậy với mọi điểm O, ta có \(\overrightarrow {OA}  + \overrightarrow {OB}  + 2\overrightarrow {OC}  = 4\overrightarrow {OM} \).

Tham khảo cách 2 câu a: 

Cách 2:

Ta có: \(\overrightarrow {MA}  + \overrightarrow {MB}  + 2\overrightarrow {MC}  = \overrightarrow 0  \Leftrightarrow \left( {\overrightarrow {MC}  + \overrightarrow {CA} } \right) + \left( {\overrightarrow {MC}  + \overrightarrow {CB} } \right) + 2\overrightarrow {MC}  = \overrightarrow 0 \)

\(\begin{array}{l} \Leftrightarrow 4\overrightarrow {MC}  + \overrightarrow {CA}  + \overrightarrow {CB}  = \overrightarrow 0 \\ \Leftrightarrow 4.\overrightarrow {CM}  = \overrightarrow {CA}  + \overrightarrow {CB} \end{array}\)

Gọi D là đỉnh thứ tư của hình bình hành ACBD.

Khi đó: \(\overrightarrow {CD}  = \overrightarrow {CA}  + \overrightarrow {CB} \)\( \Rightarrow 4.\overrightarrow {CM}  = \overrightarrow {CD} \)

\( \Leftrightarrow \overrightarrow {CM}  = \frac{1}{4}\overrightarrow {CD}  \Leftrightarrow \overrightarrow {CM}  = \frac{1}{2}\overrightarrow {CO} \)

Với O là tâm hình bình hành ACBD, cũng là trung điểm đoạn AB.

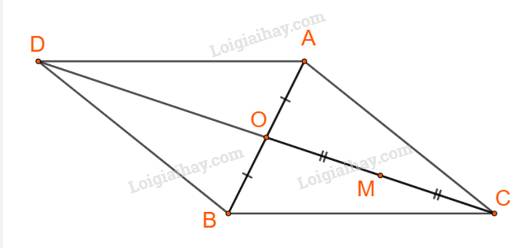
Vậy M là trung điểm của trung tuyến kẻ từ C của tam giác ABC.

Đáp án:

Giải thích các bước giải:

 Gọi G là trọng tâm của tgMBC => G trên MI và MG/IM = 2/3

Trên MN lấy điểm K sao cho MK/MN = 2/3 => Điểm K cố định và KG // NI vì MG/MI = MK/MN =2/3

=> ^MGK = ^MIN mà ^MIN không đổi (góc nội tiếp của đường tròn đk AO qua 5 điểm câu a)

=> G thuộc cung tròn cố định chứa ^MGK không đổi  nhận MK là dây

Học tốt