a)chứng minh DE // DC (hình trên)
b) chứng minh \(\widehat{ACB}=\widehat{CBF}\)
Bài 4: Cho tam giác ABC (AB = AC), đường cao BH. Từ điểm D thuộc cạnh BC kẻ DE ⊥ AB (E ∈ AB); DF ⊥ AC (F ∈ AC) và DK ⊥ BH (K ∈ BH)
a) Chứng minh: \(\widehat{KDB}=\widehat{ACB}\)
b) Chứng minh: ΔEBD = ΔKDB.
c) Chứng minh: DE + DF = BH.
d) Trên tia đối của tia CA lấy điểm P sao cho CP = HF. Chứng minh rằng trung điểm của EP nằm trên BC.
e) Cho \(\widehat{A}=40^o\), kẻ đường cao AH. Trên các đoạn thẳng AH, AC lấy thứ tự các điểm E, F sao cho \(\widehat{ABE}=\widehat{CBF}=30^o\). Tính góc AEF.
Cho tam giác nhọn ABC, đường cao AH. Gọi D và E lần lượt là hình chiếu của H trên AB và AC
a, Chứng minh : AD . AB = AE. AC
b, Chứng minh : \(\widehat{ADE}=\widehat{ACB}\)
c, Gọi O là giao điểm của AH với DE . Chứng minh; OA , OH = OD . OE
\(a,Do\Delta\)vuông AHC có:
AH2=AE.AC (1)
\(\Delta\) vuông AHB có:
AH2=AD.AB (2)
Từ (1) và (2) :
AE.AC =AD.AB
b, Xest \(\Delta\)AED và \(\Delta\)ABC có:
\(\widehat{BAC}\)chung
AE.AC=AD.AB (câu a)
=> tam giác AED đồng dạng với tam giác ABC ( c-g-c)
=> Góc ADE = góc ACB ( điều phải chứng minh )
c, Do tam giác ADE đồng dạng với tam giác ABC
=> Góc E1 = Góc B1 (1)
Mà góc B1 + góc H1 = 90 độ ( tam giác BDH vuông tại D )
Góc H1 + Góc H2 = 90 độ ( tam giác AHB vuông tại D )
=> Góc B1 = Góc H2 (2)
Từ (1) và (2) : => Góc E1 = góc H2
Xét tam giác AOE và tam giác DOH có:
Góc O1 = Góc O2 ( 2 góc đối đỉnh )
Góc E1 = góc H2 ( chứng minh trên )
=> tam giác AOE đồng dạng với tam giác DOH (g-g)
=> \(\frac{OA}{OD}=\frac{OE}{OH}\)=> OA . OH = OD . OE
Cho \(\Delta ABC\)có \(\widehat{B}=90^o\)và \(\widehat{B}=2\widehat{C}\). Kẻ đường cao AH. Trên tia dối của tia BA lấy E sao cho BE=BH. Đường thẳng HE cắt AC tại D.
a, Chứng minh \(\widehat{BEH}=\widehat{ACB}\)
b, Chứng minh DH=DC=DA
c, Lấy B' sao cho H là trung điểm của BB' . Chứng minh \(\Delta AB'C\)cân
d, Chứng minh AE=HC
viết đúng đầu bài ra ĐƯỜNG CAO AH NHƯ VẬY H SẼ TRÙNG VỚI B
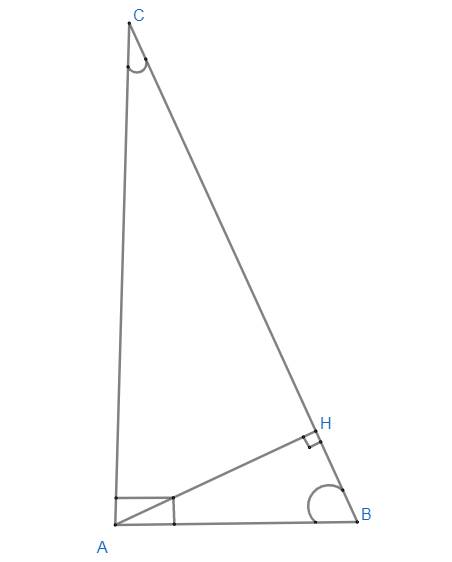
Cho ΔABC vuông tại A (AB < AC)
Kẻ \(AH\perp BC\) tại H
a) Chứng minh \(\widehat{ABC}\) = \(\widehat{HAC}\)
b) Chứng minh \(\widehat{ACB}\) = \(\widehat{HAB}\)
a)
Xét 2 tam giác vuông ABC và HAC có:
\(\widehat{C}\) chung
=> tg ABC \(\sim\) td HAC (g.g)
=> \(\widehat{ABC}=\widehat{HAC}\)
b)
Xét 2 tg vuông ACB và HAB có:
\(\widehat{B}\) chung
=> tg ACB \(\sim\) tg HAB (g.g)
=> \(\widehat{ACB}=\widehat{HAB}\)
Cho \(\Delta ABC\)có \(\widehat{B}< 90^o\)và \(\widehat{B}=2\widehat{C}\). Kẻ đường cao AH. Trên tia dối của tia BA lấy E sao cho BE=BH. Đường thẳng HE cắt AC tại D.
a, Chứng minh \(\widehat{BEH}=\widehat{ACB}\)
b, Chứng minh DH=DC=DA
c, Lấy B' sao cho H là trung điểm của BB' . Chứng minh \(\Delta AB'C\)cân
d, Chứng minh AE=HC
Cho Hình 43 có AB = AD, \(\widehat {ABC} = \widehat {ADC} = 90^\circ \). Chứng minh \(\widehat {ACB} = \widehat {ACD}\).
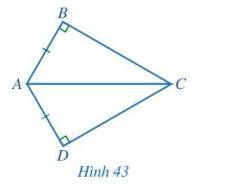
Xét hai tam giác vuông ABC và ADC có: AB = AD, AC chung.
Nên \(\Delta ABC = \Delta ADC\) (cạnh huyền - cạnh góc vuông) nên \(\widehat {ACB} = \widehat {ACD}\) (2 góc tương ứng)
Cho tam giác ABC có \(\widehat{ABC}\)=\(\widehat{ACB}\)=700 và đường cao AH. Các điểm E, F theo thứ tự thuộc các đoạn AH, AC sao cho \(\widehat{ABE}\)=\(\widehat{CBF}\)=300. Gọi M là trung điểm của AB.
a) Chứng minh \(\Delta AMF\)đồng dạng \(\Delta BHE\)
b) Chứng minh AB.BE= BC. AE
Cho tam giác ABC có \(\widehat{B}\)<90 độ và \(\widehat{B}\) = 2\(\widehat{C}\)Kẻ đường cao AH. Trên tia đối của tia BA lấy điểm E sao cho BE=BH. Đường thẳng HE cắt AC tại D.
a. Chứng minh \(\widehat{BEH}\)= \(\widehat{ACB}\)
b. Chứng minh DH=DC=DA
c. Lấy B' sao cho H là trung điểm của BB'. Chứng minh tam giác AB'C cân
d. Chứng minh AE=HC
Mình chỉ cần câu b,c,d thôi nhé. Tick cho bạn trả lời đúng
Cho △ABC vuông tại A, AB = 6cm, AC = 8cm.
a) Tính BC
b) Đường thẳng đi qua trung điểm I của BC và vuông góc với BC cắt AC tại D. Chứng minh \(\widehat{CBD}\) = \(\widehat{DCB}\)
c) Trên tia đối của tia DB lấy điểm E sao cho DE = DC. Chứng minh △BCE vuông
Cho tam giác ABC có \(\widehat{B}< 90^o\) và \(\widehat{B}=2.\widehat{C}\). Kẻ đường cao AH. Trên tia đối của tia BA lấy điểm E sao cho BE = BH. Đường thẳng HE cắt AC tại D.
1, Chứng minh : \(\widehat{BEH}=\widehat{ACB}\)
2, So sánh độ dài của ba đoạn thẳng : DH; DC và DA.
3, Lấy B' sao cho H là trung điểm của BB'.
Tam giác AB'C là tam giác gì? Vì sao?
4, Chứng minh : Nếu tam giác ABC vuông tại A thì \(DE^2=BC^2-AB^2\)
Bạn tự vẽ hình nha
1. Xét tam giác EBH có: BE=BH (gt) -> tan giác EBH cân tại B -> góc BEH = góc BHE
Ta lại có góc ABH = góc BEH + góc BHE (góc ngoài của tam giác EBH); Mà góc BEH = góc BHE (cmt) -> góc ABH = 2 góc BEH; Mà góc ABH = 2 góc ACB (gt)-> góc BEH = góc ACB ( đpcm)
2. Ta có: góc BHE = góc DHC (2 góc đối đỉnh); Mà góc BHE = góc BEH (cmt) và góc BEH = góc ACB (cmt) => góc DHC = góc ACB -> tam giác DHC cân tại D -> DH = DC ( 2 cạnh tương ứng)
Ta có: tam giác AHC vuông tại H -> góc HAC +góc ACB = 90 độ (2 góc ở đáy tam giác vuông ); Mà góc AHD + góc DHC = 90 độ và góc ACB = góc DHC (cmt) -> góc HAC = góc AHD -> tam giác AHD cân tại D => DA = DH (2 cạnh tương ứng )
Vậy DH=DC=DA
3. Ta có tam giác ABB' có: BH = B'H ( H là trung điểm BB') -> AH là đường trung tuyến lại vừa là đường cao -> tam giác ABB' cân tại A -> góc ABH = góc AB'H (2 góc ở đáy)
Xét tam giác AB'C có: góc AB'H = góc B'AC + góc ACB' (góc ngoài); Mà góc ABH = góc AB'H (cmt) -> góc ABH = góc B'AC + góc ACB ; Mà góc ABH = 2 góc ACB'
-> góc B'AC = góc ACB' => tam giác AB'C cân tại B'
4. Bạn vẽ lại hình nha: giả sử tam giác ABC vuông tại A
Xét tam giác ADE và tam giác ABC có: góc A chung và góc BEH = góc ACB (cmt) -> hai tam giác đồng dạng theo trường hợp (g.g) -> góc ADE = góc ABC (2 góc tương ứng) (1)
Ta có : góc HAD = 90 độ - góc C ( tam giác HAC vuông tại H); Mà góc ABC = 90 độ - góc C ( tam giác ABC vuông tại A) -> góc HAD = góc ABC (2)
Từ (1) và (2) -> góc ADE = góc HAD; Mà góc HAD = góc AHD nên suy ra tam giác AHD đều
Xét tam giác ADE và tâm giác HAC có: góc EAD = góc CHA = 90 độ (gt); góc ADE = góc HAC (cmt); AD = AH (tam giác AHD đều) => tam giác ADE = tam giác HAC theo trường hợp (g.c.g)
=> DE = AC (2 cạnh tương ứng) => DE2 = AC2 ; Mà AC2 = BC2 - AB2 (định lí Py-ta-go trong tam giác ABC) => DE2 = BC2 - AB2 (đpcm)
Học tốt nhé 🙋♀️🙋♀️🙋♀️💗💗💗