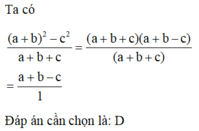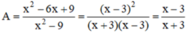rút gọn phân thức : a) A = 6x2y2 / 8xy5

Những câu hỏi liên quan
Bài 2 rút gọn các biểu thức sau
A)(2x+3y)(x-2y)-(4x3y-6x2y2-3xy3):2xy
B) (x-2)3 -x(x+1)(x-1)-(3x-1)(3x-2)
a: \(\left(2x+3y\right)\left(x-2y\right)-\dfrac{\left(4x^3y-6x^2y^2-3xy^3\right)}{2xy}\)
\(=2x^2-4xy+3xy-6y^2-\dfrac{2xy\cdot\left(2x^2-3xy-1,5y^2\right)}{2xy}\)
\(=2x^2-xy-6y^2-2x^2+3xy+1,5y^2\)
\(=2xy-4,5y^2\)
b: \(\left(x-2\right)^3-x\left(x+1\right)\left(x-1\right)-\left(3x-1\right)\left(3x-2\right)\)
\(=x^3-6x^2+12x-8-x\left(x^2-1\right)-\left(9x^2-6x-3x+2\right)\)
\(=x^3-6x^2+12x-8-x^3+x-9x^2+9x-2\)
\(=-15x^2+22x-10\)
Đúng 1
Bình luận (0)
Tính và thu gọn : 3x2(3x2-2y2)-(3x2-2y2)(3x2+2y2) được kết quả là :
a/ 6x2y2-4y4 b/ -6x2y2+4y4 c/-6x2y2-4y4 d/ 18x4 -4y4
Mn giúp tôi với
\(3x^2\left(3x^2-2y^2\right)-\left(3x^2-2y^2\right)\left(3x^2+2y^2\right)\)
\(=9x^4-6x^2y^2-9x^4+4y^4\)
\(=-6x^2y^2+4y^4\)
Đúng 0
Bình luận (1)
a) Thay phân thức
P
uv
u
−
v
vào biểu thức
A
uP
u
+
P
−
vP
v
−
P
rồi rút gọn;b) Thay hai phân thức
P
2
mn...
Đọc tiếp
a) Thay phân thức P = uv u − v vào biểu thức A = uP u + P − vP v − P rồi rút gọn;
b) Thay hai phân thức P = 2 mn m 2 + n 2 và Q = 2 mn m 2 + n 2 vào biểu thức B = P 2 Q 2 P 2 − Q 2 rồi rút gọn;
a) Thay phân thức P vào biểu thức A rồi rút gọn chúng ta thu được A = u + v với điều kiện các biểu thức có nghĩa.
b) Tương tự a) ta có B = 1.
Đúng 0
Bình luận (0)
\(A=\dfrac{x^2-2x+1}{x^2-1}\)
a) tìm điều kiên xác định của phân thức
b)rút gọn phân thức
c)tính giá trị của phân thức tại x=3
BÀI5
\(B=\dfrac{6x-2y}{9x^2-y^2}\)
a)tìm điều kiện xác định của phân thức
b)rút gọn phân thức
c)tính giá trị của phân thức tại x=1 y=-1/2
a) ĐKXĐ:
\(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
b) \(A=\dfrac{x^2-2x+1}{x^2-1}\)
\(A=\dfrac{x^2-2\cdot x\cdot1+1^2}{x^2-1^2}\)
\(A=\dfrac{\left(x-1\right)^2}{\left(x+1\right)\left(x-1\right)}\)
\(A=\dfrac{x-1}{x+1}\)
c) Thay x = 3 vào A ta có:
\(A=\dfrac{3-1}{3+1}=\dfrac{2}{4}=\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
a) ĐKXĐ:
\(9x^2-y^2\ne0\Leftrightarrow\left(3x\right)^2-y^2\ne0\Leftrightarrow\left(3x-y\right)\left(3x+y\right)\ne0\)
\(\Leftrightarrow3x\ne\pm y\)
b) \(B=\dfrac{6x-2y}{9x^2-y^2}\)
\(B=\dfrac{2\cdot3x-2y}{\left(3x\right)^2-y^2}\)
\(B=\dfrac{2\left(3x-y\right)}{\left(3x+y\right)\left(3x-y\right)}\)
\(B=\dfrac{2}{3x+y}\)
Thay x = 1 và \(y=\dfrac{1}{2}\) và B ta có:
\(B=\dfrac{2}{3\cdot1+\dfrac{1}{2}}=\dfrac{2}{3+\dfrac{1}{2}}=\dfrac{2}{\dfrac{7}{2}}=\dfrac{4}{7}\)
Đúng 1
Bình luận (0)
Rút gọn phân thức
(a
+
b)
2
−
c
2
a
+
b
+
c
ta được phân thức có tử là? A. a - b - c B. a +b + c C. a - b + c D. a + b - c
Đọc tiếp
Rút gọn phân thức (a + b) 2 − c 2 a + b + c ta được phân thức có tử là?
A. a - b - c
B. a +b + c
C. a - b + c
D. a + b - c
Cho phân thức A = x 2 - 6 x + 9 x 2 - 9
b) Rút gọn A
cho phân thức A=\(\dfrac{4x+4}{x2-1}\)
a) tìm x để phân thức A có nghĩa
b)rút gọn phân thức A
c) tính giá trị của phân thức A tại x=5
d) Tìm x để giá trị của phân thức A bằng 3
a) \(\text{A}=\dfrac{4x+4}{x^2-1}.\)
Để phân thức A có nghĩa. \(\Leftrightarrow x\ne1;x\ne-1.\)
b) \(\text{A}=\dfrac{4x+4}{x^2-1}=\dfrac{4\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{x-1}.\)
Đúng 0
Bình luận (0)
Phân tích đa thức
x
3
y
3
+
6
x
2
y
2
+
12
x
y
+
8
thành nhân tử ta được A.
(
x
y
+
2
)...
Đọc tiếp
Phân tích đa thức x 3 y 3 + 6 x 2 y 2 + 12 x y + 8 thành nhân tử ta được
A. ( x y + 2 ) 3
B. ( x y + 8 ) 3
C. x 3 y 3 + 8
D. x 3 y 3 + 2 3
Ta có
x 3 y 3 + 6 x 2 y 2 + 12 x y + 8 = ( x y ) 3 + 3 ( x y ) 2 . 2 + 3 x y . 2 2 + 2 3 = ( x y + 2 ) 3
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
RÚT GỌN
\(P=\frac{2x^2-8}{x-2}\)
a) rút gọn phân thức P
b) tìm giá trị của x để giá trị của phân thức P =2
\(P=\frac{2x^2-8}{x-2}=\frac{2.\left(x^2-2^2\right)}{x-2}=\frac{2.\left(x-2\right).\left(x+2\right)}{x-2}=2x+4\left(x\ne2\right)\)
\(P=2x+4=2\Rightarrow2x=-2\Rightarrow x=-1\)
Đúng 0
Bình luận (0)
Cho phân thức \(\dfrac{x^2-10x+25}{x^2-5x}\)
a. Tìm điều kiện xác định của phân thức
b. Rút gọn phân thức
a. \(x^2-5x\ne0\)
=> ĐKXĐ: \(x\left(x-5\right)\ne0\) => \(\left\{{}\begin{matrix}x\ne0\\x\ne5\end{matrix}\right.\)
b. \(\dfrac{x^2-10x+25}{x^2-5x}\)
= \(\dfrac{\left(x-5\right)^2}{x\left(x-5\right)}\)
= \(\dfrac{x-5}{x}\)
Đúng 2
Bình luận (0)