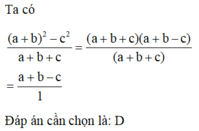Các câu hỏi tương tự
1/ Cho a,b,c đối 1 khác nhau thỏa mãn điều kiện (a + b + c)^2 = a^2 + b^2 + c^2 (^ là mũ)
Rút gọn biểu thức: P= (a^2)/(a^2+2bc) + (b^2)/(b^2+2ac)+(c^2)/(c^2+2ab)
2/ Phân tích đa thức thành nhân tử: (x + 1)^4 + (x^2 + x +1)^2
3/ Phân tích đa thức thành nhân tử: ab(a - b) + bc(b - c) + ca(c - a)
Cho phân thức
M=(a2+b2+c2)(a+b+c)2+(ab+bc+ac)2/(a+b+c)2-(ab+bc+ac)
a)Tìm giá trị của a,b,c để phân thức được xác định
b)Rút gọn phân thức M
Rút Gọn phân thức sau: {a^3(b^2-c^2)+b^3(c^2-a^2)+c^3(a^2-b^2)}/{a^2(b-c)+b^2(c-a)+c^2(a-b)}
CHo phân thức \(M=\frac{\left(a^2+b^2+c^2\right)\left(a+b+c\right)^2+\left(ab+bc+ca\right)^2}{\left(a+b+c\right)^2-\left(ab+bc+ca\right)}\)
a) Tìm các giá trị của a,b,c phân thức có nghĩa.
b) Rút gọn phân thức M
rút gọn phân thức \(\dfrac{\left(a+b\right)^2-c^2}{a+b+c}\)
Rút gọn phân thức :
A = 1 / (a - b )(a - c) + 1/ (b - c)(b - a) +1/(c - a)(c - b)
Cho phân thức sau:
\(\dfrac{\left(a^2+b^2+c^2\right)\left(a+b+c\right)^2+\left(ab+bc+ca\right)^2}{\left(a+b+c\right)^2-\left(ab+bc+ca\right)}\)
a. Tìm giá trị a,b,c để phân thức có nghĩa
b. Thu gọn phân thức
Rút gọn phân thức:
a/\(\frac{a^2\left(b-c\right)+b^2\left(c-a\right)+c^2\left(a-b\right)}{a^4\left(b^2-c^2\right)+b^2\left(c^2-a^2\right)+c^4\left(a^2-b^2\right)}\)
Rút gọn phân thức:
\(A=\frac{\left(b-c\right)^3+\left(c-a\right)^3+\left(a-b\right)^3}{a^2\left(b-c\right)+b^2\left(c-a\right)+c^2\left(a-b\right)}\)