a: AB=BC=CD=DA=6a

\(AC=BD=\sqrt{\left(6a\right)^2+\left(6a\right)^2}=6a\sqrt{2}\)

\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=CB=6a\)

\(\left|\overrightarrow{BC}+\overrightarrow{BD}\right|=\sqrt{BC^2+BD^2+2\cdot BC\cdot BD\cdot cos45}\)

\(=\sqrt{36a^2+72a^2+\sqrt{2}\cdot6a\cdot6a\sqrt{2}}\)

\(=6a\sqrt{5}\)

b: \(\overrightarrow{AB}\cdot\overrightarrow{AC}=AB\cdot AC\cdot cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=6a\cdot6a\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}\)

\(=36a^2\)

Tham khảo:

\(\overrightarrow {CD}  = \overrightarrow {BA} \) do hai vectơ \(\overrightarrow {CD} ,\;\overrightarrow {BA} \) cùng hướng và \(CD = BA\).

\(\begin{array}{l} \Rightarrow \overrightarrow {CB}  + \overrightarrow {CD}  = \overrightarrow {CB}  + \overrightarrow {BA}  = \overrightarrow {CA} \\ \Leftrightarrow \left| {\overrightarrow {CB}  + \overrightarrow {CD} } \right| = \left| {\overrightarrow {CA} } \right| = CA\end{array}\)

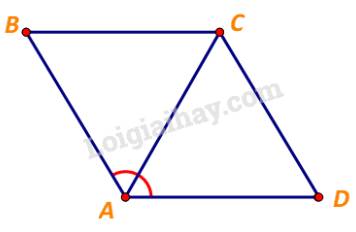
Xét tam giác ABC, ta có:

\(BA = BC\) và \(\widehat {BAC} = \frac{1}{2}.\widehat {BAD} = {60^o}\)

\( \Rightarrow \Delta ABC\) đều, hay \(CA = BC = 1\)

Vậy \(\left| {\overrightarrow {CB}  + \overrightarrow {CD} } \right| = 1.\)

Dựa vào tính chất kết hợp, ta có:

\(\begin{array}{l}\overrightarrow {DB}  + \overrightarrow {CD}  + \overrightarrow {BA}  = \left( {\overrightarrow {DB}  + \overrightarrow {CD} } \right) + \overrightarrow {BA} \\ = \left( {\overrightarrow {CD}  + \overrightarrow {DB} } \right) + \overrightarrow {BA}  = \overrightarrow {CB}  + \overrightarrow {BA}  = \overrightarrow {CA} .\\ \Rightarrow \left| {\overrightarrow {DB}  + \overrightarrow {CD}  + \overrightarrow {BA} } \right| = \left| {\overrightarrow {CA} } \right| = CA = 1.\end{array}\)

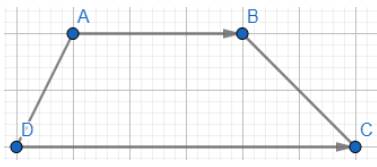
Áp dụng quy tắc ba điểm ta có:

\(\overrightarrow a  = \overrightarrow {AC}  + \overrightarrow {CB}  = \overrightarrow {AB} \); \(\overrightarrow b  = \overrightarrow {DB}  + \overrightarrow {BC}  = \overrightarrow {DC} \)

Mà ABCD là hình thang nên AB//DC. Mặt khác vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \) đều có hướng từ trái sang phải, suy ra vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \)cùng hướng

Vậy hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.

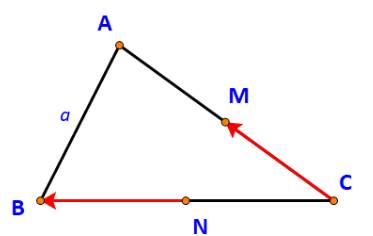
Ta có: \(\overrightarrow {NB} \) và \(\overrightarrow {NC} \) là hai vecto đối nhau (do N là trung điểm của BC)

\( \Rightarrow \overrightarrow {NC}  =  - \overrightarrow {NB} \)

Do đó: \(\overrightarrow {CM}  - \overrightarrow {NB}  = \overrightarrow {CM}  + \overrightarrow {NC}  = \overrightarrow {NC}  + \overrightarrow {CM} \)(tính chất giáo hoán)

\( \Rightarrow \overrightarrow {CM}  - \overrightarrow {NB}  = \overrightarrow {NM}  \Leftrightarrow \;|\overrightarrow {CM}  - \overrightarrow {NB} |\, = \;|\overrightarrow {NM} | = NM.\)

Vì: M, N lần lượt là trung điểm của AC, BC nên \(MN = \frac{1}{2}AB = \frac{a}{2}.\)

Vậy \(\;|\overrightarrow {CM}  - \overrightarrow {NB} |\, = \frac{a}{2}.\)

1: \(=\left|\overrightarrow{CO}-\overrightarrow{CB}\right|=BO=\dfrac{a\sqrt{2}}{2}\)

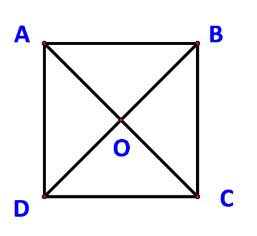
a) Do ABCD cũng là một hình bình hành nên \(\overrightarrow {DA}  + \overrightarrow {DC}  = \overrightarrow {DB} \)

\( \Rightarrow \;|\overrightarrow {DA}  + \overrightarrow {DC} |\; = \;|\overrightarrow {DB} |\; = DB = a\sqrt 2 \)

b) Ta có: \(\overrightarrow {AD}  + \overrightarrow {DB}  = \overrightarrow {AB} \) \( \Rightarrow \overrightarrow {AB}  - \overrightarrow {AD}  = \overrightarrow {DB} \)

\( \Rightarrow \left| {\overrightarrow {AB}  - \overrightarrow {AD} } \right| = \left| {\overrightarrow {DB} } \right| = DB = a\sqrt 2 \)

c) Ta có: \(\overrightarrow {DO}  = \overrightarrow {OB} \)

\( \Rightarrow \overrightarrow {OA}  + \overrightarrow {OB}  = \overrightarrow {OA}  + \overrightarrow {DO}  = \overrightarrow {DO}  + \overrightarrow {OA}  = \overrightarrow {DA} \)

\( \Rightarrow \left| {\overrightarrow {OA}  + \overrightarrow {OB} } \right| = \left| {\overrightarrow {DA} } \right| = DA = a.\)

\(\overrightarrow{BA}+\overrightarrow{BC}+2\overrightarrow{DO}=\overrightarrow{BD}+\overrightarrow{DB}=\overrightarrow{0}\)

\(\overrightarrow{CM}=\frac{\overrightarrow{CA}+\overrightarrow{CB}}{2}=\frac{1}{4}\left(\overrightarrow{CD}+\overrightarrow{CB}\right)+\frac{1}{2}\overrightarrow{CB}=\frac{1}{4}\overrightarrow{CD}+\frac{3}{4}\overrightarrow{CB}\)