Trong mặt phẳng toạ độ Oxy, cho hai điểm M(1/3;1/2), N(4/3;5/2). Tìm toạ độ giao điểm I của MN và trục Oy
a) Tính khoảng cách từ gốc toạ độ C(0;0) đến điểm M(3 ; 4) trong mặt phẳng toạ độ Oxy.
b) Cho hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy. Nêu công thức tính độ dài đoạn thẳng IM.
a) Khoảng cách từ gốc tọa độ \(O\left( {0;0} \right)\) đến điểm \(M\left( {3;4} \right)\) trong mặt phẳng tọa độ Oxy là:
\(OM = \left| {\overrightarrow {OM} } \right| = \sqrt {{3^2} + {4^2}} = 5\)
b) Với hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy, ta có:\(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2}} \)
1. Trong mặt phẳng với hệ toạ độ Oxy, viết phương trình đường thẳng △ song song với đường thẳng d: 2x-y+2015=0 và cắt hai trục toạ độ tại M và N sao cho MN=3√5
2.Trong mặt phẳng với hệ toạ độ Oxy, cho 2 điểm A(1;2) ; B(4;3). Tìm toạ độ điểm M sao cho ∠MAB=135 độ và khoảng cách từ M đến đường thẳng AB bằng √10/2
Câu 1:
Do \(\Delta\) song song d nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình \(\Delta\) có dạng: \(2x-y+c=0\) (\(c\ne2015\))
Tọa độ giao điểm của \(\Delta\) và Ox: \(\left\{{}\begin{matrix}y=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{c}{2};0\right)\)
Tọa độ giao điểm \(\Delta\) và Oy: \(\left\{{}\begin{matrix}x=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow N\left(0;c\right)\)
\(\overrightarrow{MN}=\left(\frac{c}{2};c\right)\Rightarrow\frac{c^2}{4}+c^2=45\Leftrightarrow c^2=36\Rightarrow\left[{}\begin{matrix}c=6\\c=-6\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}2x-y+6=0\\2x-y-6=0\end{matrix}\right.\)
Bài 2:
Bạn tham khảo ở đây:
Câu hỏi của tôn hiểu phương - Toán lớp 10 | Học trực tuyến
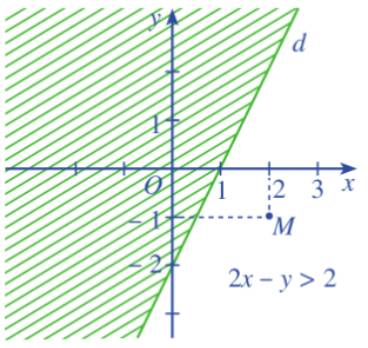
Cho bất phương trình 2x – y>2 (3).
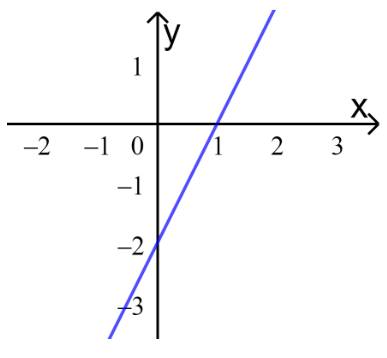
a) Trong mặt phẳng toạ độ Oxy, vẽ đường thẳng \(d:2x - y = 2 \Leftrightarrow y = 2x - 2\).
b) Xét điểm M(2;-1). Chứng tỏ (2;-1) là nghiệm của bất phương trình (3).
c) Đường thẳng d chia mặt phẳng toạ độ thành hai nửa mặt phẳng. Gạch đi nửa mặt phẳng không chứa điểm M(2;- 1).
a) Cho \(x=0\Rightarrow y=-2\)
Cho \(y=0\Rightarrow x=1\)
Nối hai điểm (0;-2) và (1;0) ta được:
b) Thay tọa độ điểm M vào bất phương trình (3) ta được:
\(2.2 - \left( { - 1} \right) > 2 \Leftrightarrow 5 > 2\)(Luôn đúng)
Vậy (2;-1) là một nghiệm của bất phương trình (3)
c) Ta gạch đi nửa mặt phẳng không chứa M được:
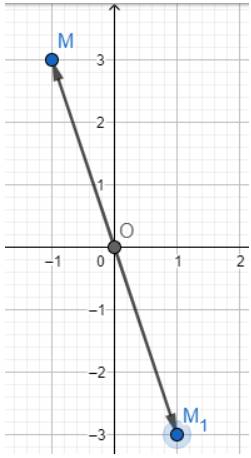
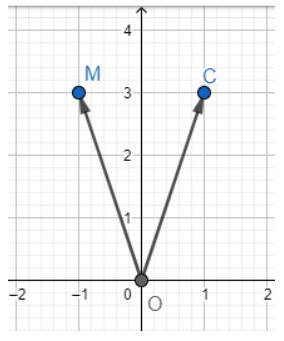
Trong mặt phẳng toạ độ Oxy, cho điểm M(-1; 3).
a) Tìm toạ độ điểm A đối xứng với điểm M qua gốc O.
b) Tìm toạ độ điểm B đối xứng với điểm M qua trục Ox.
c) Tìm toạ độ điểm C đối xứng với điểm M qua trục Oy.
a) Dựa vào hình vẽ ta thấy \(A\left( {1; - 3} \right)\)
b) Dựa vào hình vẽ ta thấy \(B\left( { - 1; - 3} \right)\)

c) Dựa vào hình vẽ ta thấy \(C\left( {1;3} \right)\)
14. Trong mặt phẳng toạ độ Oxy , cho hai điểm A(3;-4) , B(0;6). Viết pt tham số của đg thẳng AB.
15. Trong mặt phẳng toạ độ Oxy , viết pt tham số của đg thẳng d đi qua điểm A(0;-4) và song song vs đg thẳng denta có pt tham số : x = 2018 + 2t ; y = 10 - t
18. Trong mặt phẳng toạ độ Oxy , lập pt tổng quát của đg thẳng d biết d đi qua M(-1;0) và có vectơ chỉ phương v = (2;3)
19. Trong mặt phẳng toạ độ Oxy , lập pt tổng quát của đg thẳng d biết d đi qua điểm A(-2;4) và B(1;0).
14.
\(\overrightarrow{AB}=\left(-3;10\right)\) nên pt tham số của AB là: \(\left\{{}\begin{matrix}x=3-3t\\y=-4+10t\end{matrix}\right.\)
15.
Do d song song delta nên d nhận \(\left(2;-1\right)\) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=2t\\y=-4-t\end{matrix}\right.\)
18.
d có vtcp là (2;3) nên d nhận (3;-2) là 1 vtpt
Phương trình d:
\(3\left(x+1\right)-2\left(y-0\right)=0\Leftrightarrow3x-2y+3=0\)
19.
\(\overrightarrow{AB}=\left(3;-4\right)\Rightarrow\) đường thẳng AB nhận (4;3) là 1 vtpt
Phương trình d:
\(4\left(x+2\right)+3\left(y-4\right)=0\Leftrightarrow4x+3y-4=0\)
Trong mặt phẳng toạ độ Oxy cho hai điểm A B (3; 1), (2; 10). Tích vô hướng OA.OB bằng bao nhiêu
\(\overrightarrow{OA}=\left(3;1\right);\overrightarrow{OB}=\left(2;10\right)\)
\(\overrightarrow{OA}\cdot\overrightarrow{OB}=3\cdot2+1\cdot10=16\)
Trong mặt phẳng toạ độ Oxy, cho ba điểm A(2;3), B(-1; 1), C(3;- 1).
a) Tìm toạ độ điểm M sao cho\(\overrightarrow {AM{\rm{ }}} = {\rm{ }}\overrightarrow {BC} \).
b) Tìm toạ độ trung điểm N của đoạn thẳng AC. Chứng minh\(\overrightarrow {BN} {\rm{ }} = {\rm{ }}\overrightarrow {NM} \).
a) Gọi \(M\left( {a;b} \right) \Rightarrow \overrightarrow {AM} = \left( {a - 2;b - 3} \right)\)
Tọa độ vecto \(\overrightarrow {BC} = \left( {4; - 2} \right)\)
Để \(\overrightarrow {AM{\rm{ }}} = {\rm{ }}\overrightarrow {BC} \Leftrightarrow \left\{ \begin{array}{l}a - 2 = 4\\b - 3 = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 6\\b = 1\end{array} \right.\)
Vậy để \(\overrightarrow {AM{\rm{ }}} = {\rm{ }}\overrightarrow {BC} \) thì tọa độ điểm M là:\(M\left( {6;1} \right)\)
b) Gọi \(N\left( {x,y} \right) \Rightarrow \overrightarrow {NC} = \left( {3 - x, - 1 - y} \right)\)và \(\overrightarrow {AN} = \left( {x - 2,y - 3} \right)\)
Do N là trung điểm AC nên \(\overrightarrow {AN} = \overrightarrow {NC} \Leftrightarrow \left\{ \begin{array}{l}x - 2 = 3 - x\\y - 3 = - 1 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{5}{2}\\y = 1\end{array} \right.\) . Vậy \(N\left( {\frac{5}{2},1} \right)\)
Ta có: \(\overrightarrow {BN} {\rm{ }} = \left( { \frac{7}{2};0} \right)\) và \(\overrightarrow {NM} = \left( {\frac{{ 7}}{2};0} \right)\). Vậy \(\overrightarrow {BN} {\rm{ }} = {\rm{ }}\overrightarrow {NM} \)
Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng A(- 3 ; 1), B(-1; 3), I(4;2). Tìm toạ độ của hai điểm C, D sao cho tứ giác ABCD là hình bình hành nhận I làm tâm đối xứng.
Gọi \(C\left( {a;b} \right),D\left( {m,n} \right) \Rightarrow \overrightarrow {IC} = \left( {a - 4,b - 2} \right)\) và \(\overrightarrow {ID} = \left( {m - 4,n - 2} \right)\)
Do I là tâm của hình bình hành ABCD nên I là trung điểm AC và BD.
Vậy ta có:\(\overrightarrow {AI} = \overrightarrow {IC} \)và \(\overrightarrow {BI} = \overrightarrow {ID} \)
Ta có: \(\overrightarrow {AI} = \left( {7;1} \right)\) và \(\overrightarrow {BI} = \left( {5; - 1} \right)\)
Do \(\overrightarrow {AI} = \overrightarrow {IC} \Leftrightarrow \left\{ \begin{array}{l}7 = a - 4\\1 = b - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 11\\b = 3\end{array} \right.\) .Vậy \(C\left( {11;3} \right)\)
Do \(\overrightarrow {BI} = \overrightarrow {ID} \Leftrightarrow \left\{ \begin{array}{l}5 = m - 4\\ - 1 = n - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 9\\n = 1\end{array} \right.\). Vậy \(D\left( {9;1} \right)\)
Trong mặt phẳng với hệ trục toạ độ Oxy,cho hai điểm A(1;1),B(-4;3) và đường thẳng d:x-2y-1=0.Tìm điểm M thuộc d có toạ độ nguyên sao cho khoảng cách từ M đến đường thẳng AB bằng 6