a: \(\overrightarrow{BA}-\overrightarrow{BC}=\overrightarrow{BA}+\overrightarrow{CB}=\overrightarrow{CA}\)

b: lấy điểm H sao cho \(\overrightarrow{AH}=\overrightarrow{GC}\)

\(\overrightarrow{AH}=\overrightarrow{GC}\)

=>AH//GC và AH=GC

Xét tứ giác AHCG có

AH//CG

AH=GC

Do đó: AHCG là hình bình hành

ΔABC đều có G là trọng tâm

nên \(AG=GB=GC=\dfrac{a\sqrt{3}}{3}\)

\(\left|\overrightarrow{AB}-\overrightarrow{GC}\right|=\left|\overrightarrow{AB}-\overrightarrow{AH}\right|\)

\(=\left|\overrightarrow{HA}+\overrightarrow{AB}\right|=\left|\overrightarrow{HB}\right|=HB\)

AHCG là hình bình hành

=>HC=AG và HC//AG

=>\(HC=\dfrac{a\sqrt{3}}{3}\)

ΔABC đều có G là trọng tâm

nên GB=GC=GA

GB=GC

AB=AC

Do đó: AG là đường trung trực của BC

=>AG\(\perp\)BC

mà CH//AG

nên CH\(\perp\)CB

=>ΔCHB vuông tại C

=>\(BH^2=HC^2+BC^2\)

=>\(BH^2=\left(\dfrac{a\sqrt{3}}{3}\right)^2+a^2=a^2+\dfrac{1}{3}a^2=\dfrac{4}{3}a^2\)

=>\(BH=a\cdot\dfrac{2\sqrt{3}}{3}\)

=>\(\left|\overrightarrow{AB}-\overrightarrow{GC}\right|=BH=\dfrac{2a\sqrt{3}}{3}\)

Tham khảo:

a)  \(\)\(\overrightarrow {BA}  + \overrightarrow {AC}  = \overrightarrow {BC}  \Rightarrow \left| {\overrightarrow {BC} } \right| = BC = a\)

b) Dựng hình bình hành ABDC, giao điểm của hai đường chéo là O ta có:

\(\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {AD} \)

\(AD = 2AO = 2\sqrt {A{B^2} - B{O^2}}  = 2\sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}}  = a\sqrt 3 \)

\( \Rightarrow \left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD = a\sqrt 3 \)

c) \(\overrightarrow {BA}  - \overrightarrow {BC}  = \overrightarrow {BA}  + \overrightarrow {CB}  = \overrightarrow {CB}  + \overrightarrow {BA}  = \overrightarrow {CA} \)

\( \Rightarrow \left| {\overrightarrow {BA}  - \overrightarrow {BC} } \right| = \left| {\overrightarrow {CA} } \right| = CA = a\)

Chị ơi giúp e cái này tìm 3  giá trị của x sao cho 0,6<x<0,61

Gọi I là tâm đường tròn nội tiếp tam giác ABC

\(\Rightarrow a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}=0\)

Ta có:

\(A=\left|a\overrightarrow{MA}+b\overrightarrow{MB}+c\overrightarrow{MC}\right|=\left|\left(a+b+c\right)\overrightarrow{MI}+a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}\right|\)

   \(=\left|\left(a+b+c\right)\overrightarrow{MI}\right|=\left(a+b+c\right).MI\)

\(Amin\Leftrightarrow MImin\)

           \(\Leftrightarrow\) M trùng I

Tham khảo:

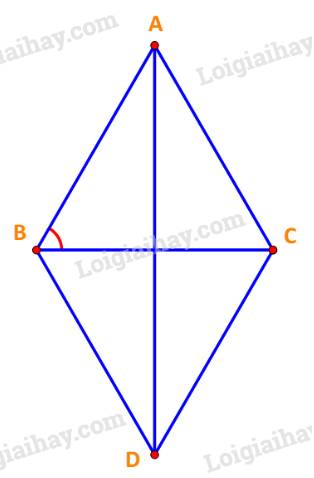
\(\overrightarrow {AB}  - \overrightarrow {AC}  = \overrightarrow {CB}  \Rightarrow \left| {\overrightarrow {AB}  - \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = CB = a.\)

Dựng hình bình hành ABDC tâm O như hình vẽ.

Ta có:

\(\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {AB}  + \overrightarrow {BD}  = \overrightarrow {AD} \)

\( \Rightarrow \left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)

Vì tứ giác ABDC là hình bình hành, lại có \(AB = AC = BD = CD = a\) nên ABDC là hình thoi.

\( \Rightarrow AD = 2AO = 2.AB.\sin B = 2a.\frac{{\sqrt 3 }}{2} = a\sqrt 3 .\)

Vậy \(\left| {\overrightarrow {AB}  - \overrightarrow {AC} } \right| = a\) và \(\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = a\sqrt 3 \).

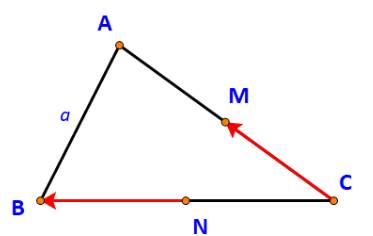
Ta có: \(\overrightarrow {NB} \) và \(\overrightarrow {NC} \) là hai vecto đối nhau (do N là trung điểm của BC)

\( \Rightarrow \overrightarrow {NC}  =  - \overrightarrow {NB} \)

Do đó: \(\overrightarrow {CM}  - \overrightarrow {NB}  = \overrightarrow {CM}  + \overrightarrow {NC}  = \overrightarrow {NC}  + \overrightarrow {CM} \)(tính chất giáo hoán)

\( \Rightarrow \overrightarrow {CM}  - \overrightarrow {NB}  = \overrightarrow {NM}  \Leftrightarrow \;|\overrightarrow {CM}  - \overrightarrow {NB} |\, = \;|\overrightarrow {NM} | = NM.\)

Vì: M, N lần lượt là trung điểm của AC, BC nên \(MN = \frac{1}{2}AB = \frac{a}{2}.\)

Vậy \(\;|\overrightarrow {CM}  - \overrightarrow {NB} |\, = \frac{a}{2}.\)

Có vẻ không đúng.

Giả sử \(\overrightarrow{AB}+\overrightarrow{MB}+\overrightarrow{MA}=\overrightarrow{0}\)

\(\Leftrightarrow\overrightarrow{MB}+\left(\overrightarrow{MA}+\overrightarrow{AB}\right)=\overrightarrow{0}\)

\(\Leftrightarrow\overrightarrow{MB}+\overrightarrow{MB}=\overrightarrow{0}\)

\(\Leftrightarrow2\overrightarrow{MB}=\overrightarrow{0}\)

\(\Leftrightarrow M\equiv B\) (Vô lí)

Hình vẽ:

a, Chứng minh \(\overrightarrow{AB}+\overrightarrow{BM}+\overrightarrow{MA}=\overrightarrow{0}\)

Ta có \(\overrightarrow{AB}+\overrightarrow{BM}+\overrightarrow{MA}=\overrightarrow{BM}+\left(\overrightarrow{MA}+\overrightarrow{AB}\right)=\overrightarrow{BM}+\overrightarrow{MB}=\overrightarrow{0}\)

b, Gọi H là trung điểm \(MC\)

Ta có \(AM=\sqrt{AC^2-MC^2}=\sqrt{4a^2-a^2}=a\sqrt{3}\)

\(AH=\sqrt{AM^2+MH^2}=\sqrt{\left(a\sqrt{3}\right)^2+\left(\dfrac{a}{2}\right)^2}=a.\dfrac{\sqrt{13}}{2}\)

\(\left|\overrightarrow{AM}+\overrightarrow{AC}\right|=\left|2\overrightarrow{AH}\right|=2AH=a\sqrt{13}\)

c, Gọi D là trung điểm AB

\(3\overrightarrow{NA}+3\overrightarrow{NB}+2\overrightarrow{NC}=3\left(\overrightarrow{NA}+\overrightarrow{NB}\right)+2\overrightarrow{NC}=6\overrightarrow{ND}+2\overrightarrow{NC}=\overrightarrow{0}\)

\(\Rightarrow\overrightarrow{NC}=3\overrightarrow{DN}\)

Vậy N thuộc đoạn CD sao cho \(CN=\dfrac{3}{4}CD\)

Dựng hình bình hành ABDC.

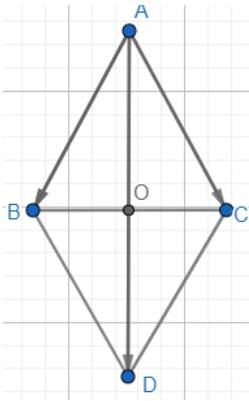
Áp dụng quy tắc hình bình hành vào ABDC ta có:

\(\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {AD}  \Rightarrow \left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)

Gọi O là giao điểm của AD và BC, ta có:

\(AO = \sqrt {A{B^2} - B{O^2}}  = \sqrt {A{B^2} - {{\left( {\frac{1}{2}BC} \right)}^2}}  = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}}  = \frac{{a\sqrt 3 }}{2}\)

\(AD = 2AO = a\sqrt 3  \Rightarrow \left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = a\sqrt 3 \)

Vậy độ dài vectơ \(\overrightarrow {AB}  + \overrightarrow {AC} \) là \(a\sqrt 3 \)