giá trị của biẻu thứcC=44.5-245-73+43 là.........?

Những câu hỏi liên quan
tìm giá trị nhỏ nhất của biểu thức
c= x2+y2-x+6x+10
\(C=x^2+y^2-x+6x+10\\ =x^2+5x+y^2+10\\ =x^2+2\cdot\dfrac{5}{2}x+\dfrac{25}{4}+y^2+\dfrac{15}{4}\\ =\left(x+\dfrac{5}{2}\right)^2+y^2+\dfrac{15}{4}\)
Mà \(\left(x+\dfrac{5}{2}\right)^2+y^2\ge0\forall x,y\)
\(\Rightarrow\left(x+\dfrac{5}{2}\right)^2+y^2+\dfrac{15}{4}\ge\dfrac{15}{4}\forall x,y\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{5}{2}=0\Leftrightarrow x=-\dfrac{5}{2}\\y=0\end{matrix}\right.\)
Vậy GTNN của C là \(\dfrac{15}{4}\) khi x = \(-\dfrac{5}{2}\) và y = 0
Đúng 0
Bình luận (0)
\(A=\dfrac{x^2-2x+1}{x^2-1}\)
a) tìm điều kiên xác định của phân thức
b)rút gọn phân thức
c)tính giá trị của phân thức tại x=3
BÀI5
\(B=\dfrac{6x-2y}{9x^2-y^2}\)
a)tìm điều kiện xác định của phân thức
b)rút gọn phân thức
c)tính giá trị của phân thức tại x=1 y=-1/2
a) ĐKXĐ:
\(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
b) \(A=\dfrac{x^2-2x+1}{x^2-1}\)
\(A=\dfrac{x^2-2\cdot x\cdot1+1^2}{x^2-1^2}\)
\(A=\dfrac{\left(x-1\right)^2}{\left(x+1\right)\left(x-1\right)}\)
\(A=\dfrac{x-1}{x+1}\)
c) Thay x = 3 vào A ta có:
\(A=\dfrac{3-1}{3+1}=\dfrac{2}{4}=\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
a) ĐKXĐ:
\(9x^2-y^2\ne0\Leftrightarrow\left(3x\right)^2-y^2\ne0\Leftrightarrow\left(3x-y\right)\left(3x+y\right)\ne0\)
\(\Leftrightarrow3x\ne\pm y\)
b) \(B=\dfrac{6x-2y}{9x^2-y^2}\)
\(B=\dfrac{2\cdot3x-2y}{\left(3x\right)^2-y^2}\)
\(B=\dfrac{2\left(3x-y\right)}{\left(3x+y\right)\left(3x-y\right)}\)
\(B=\dfrac{2}{3x+y}\)
Thay x = 1 và \(y=\dfrac{1}{2}\) và B ta có:
\(B=\dfrac{2}{3\cdot1+\dfrac{1}{2}}=\dfrac{2}{3+\dfrac{1}{2}}=\dfrac{2}{\dfrac{7}{2}}=\dfrac{4}{7}\)
Đúng 1
Bình luận (0)
Tìm giá trị nguyên của n để giá trị của biểu thức :
3n3+10n2-5 chia hết cho giá trị của biẻu thức 3n+1
\(\left(3n^3+10n^2-5\right)⋮\left(3n+1\right)\)
\(\Leftrightarrow\left[\left(3n^3+n^2\right)+\left(9n^2-1\right)-4\right]⋮\left(3n+1\right)\)
\(\Leftrightarrow\left[n^2\left(3n+1\right)+\left(3n+1\right)\left(3n-1\right)-4\right]⋮\left(3n+1\right)\)
Vì \(\left[n^2\left(3n+1\right)+\left(3n+1\right)\left(3n-1\right)\right]⋮\left(3n+1\right)\forall n\in Z\)
Để \(\left[n^2\left(3n+1\right)+\left(3n+1\right)\left(3n-1\right)-4\right]⋮\left(3n+1\right)\Leftrightarrow-4⋮\left(3n+1\right)\)
\(\Rightarrow3n+1\inƯ\left(-4\right)=\left\{-4;-2;-1;1;2;4\right\}\)
\(\Rightarrow n=\left\{-1;0;1\right\}\)
Vậy với \(n=\left\{-1;0;1\right\}\) thì \(\left(3n^3+10n^2-5\right)⋮\left(3n+1\right)\)
Đúng 0
Bình luận (0)
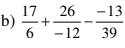
tính giá trị biẻu thức sau
\(\dfrac{17}{6}+\dfrac{26}{-12}-\dfrac{-13}{39}\)
\(=\dfrac{17}{6}-\dfrac{13}{6}+\dfrac{1}{3}\)
\(=\dfrac{4}{6}+\dfrac{1}{3}\)
\(=\dfrac{2}{3}+\dfrac{1}{3}\)
\(=1\)
| #Sahara |
Đúng 3
Bình luận (0)
Tìm giá trị lớn nhất của biểu thức
c= căn bậc 2 của x+5 + căn bậc 2 của 4-x
Bạn cần gõ đề bằng công thức toán để được hỗ trợ tốt hơn.
Đúng 0
Bình luận (0)
Tính giá trị biẻu thức:
A= 1.2 + 2.3 +3.4 +...+ 18.19
=> 3A = 1.2. (3-0) +2.3.(4-1) + ...+18.19.(20-17)
=1.2.3-0.1.2+2.3.4-1.2.3+...+18.19.20-17.18.19
=(1.2.3-1.2.3)+(2.3.4-2.3.4)+...+(17.18.19-17.18.19)+18.19.20-0.1.2
=0+0+0+...+0+18.19.20
=18.19.20
=> A = 6.19.20= 114* 20= 2280
Đúng 1
Bình luận (0)
`A= 1.2 + 2.3 +3.4 +...+ 18.19`
`3A = 1.2.3 + 2.3.(4-1) + 3.4.(5-2) +....+ 18.19.(20-17)`
`3A = 1.2.3 + 2.3.4 - 1.2.3 + 3.4.5 - 2.3.4 + ....+ 18.19.20 - 17.18.19 `
`3A = 18.19.20`
`A = 6.19.20`
`A = 2280`
Đúng 1
Bình luận (0)
Đặt `A=1.2+2.3+...+18.19`
`3A=1.2(3-0)+2.3(4-1)+...+18.19(20-17)`
`3A=1.2.3-0.1.2+2.3.4-1.2.3+...+18.19.20-17.18.19`
`3A=18.19.20=6840`
\(\Rightarrow\) `A=6840/3`
\(\Rightarrow\) `A=2280`
`@Nae`
Đúng 1
Bình luận (0)
Cho biểu thức Q = A2 - B2
a) Rút gọn biểu thức
b) Tìm điều kiện của biểu thức
c) Tính giá trị của biểu thức
\(a,Q=\left(A-B\right)\left(A+B\right)\\ b,ĐK:A,B\in R\)
Đúng 1
Bình luận (2)
Tính giá trị các biểu thức sau và viết kết quả dưới, dạng một lũy thừa của một số: D = 4 3 + 6 3 + 7 3 + 2
tính giá trị biẻu thức:|x-|x||/x



























