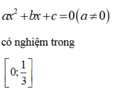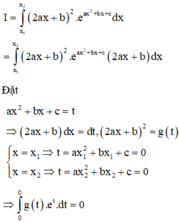Cho phương trình ax2+bx+c=0 (a≠0) có hai nghiệm x1, x2 thỏa mãn ax1+bx2+c=0. CMR: ac(a+c-3b)+b3=0.

Những câu hỏi liên quan
Cho phương trình bậc hai: ax2+bx+c=0 có hai nghiệm x1,x2thỏa mãn ax1+bx2+c=0. Tính M=a2c+ac2+b3-3abc+2018
Cho phương trình ax2 + bx + c = 0 ( a ≠ 0 ) có hai nghiệm phân biệt x1, x2thoả x1 = x2^2 . Chứng minh b3 + a 2c + ac 2 = 3abc
theo bài ra ta có
n = 8a +7=31b +28
=> (n-7)/8 = a
b= (n-28)/31
a - 4b = (-n +679)/248 = (-n +183)/248 + 2
vì a ,4b nguyên nên a-4b nguyên => (-n +183)/248 nguyên
=> -n + 183 = 248d => n = 183 - 248d (vì n >0 => d<=0 và d nguyên )
=> n = 183 - 248d (với d là số nguyên <=0)
vì n có 3 chữ số lớn nhất => n<=999 => d>= -3 => d = -3
=> n = 927
Đúng 0
Bình luận (0)
sao 2 thằng giải trên giống trong yahoo hỏi đáp vậy
Đúng 0
Bình luận (0)
Chọn phát biểu đúng: Phương trình
a
x
2
+
b
x
+
c
0
(
a
≠
0
)
có hai nghiệm
x
1
;
x
2
. Khi đó: A.
x
1
+...
Đọc tiếp
Chọn phát biểu đúng: Phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có hai nghiệm x 1 ; x 2 . Khi đó:
A. x 1 + x 2 = − b a x 1 . x 2 = c a
B. x 1 + x 2 = b a x 1 . x 2 = c a
C. x 1 + x 2 = − b a x 1 . x 2 = − c a
D. x 1 + x 2 = b a x 1 . x 2 = − c a
Cho phương trình bậc hai a x 2 + b x + c = 0 ( a ≠ 0 ) . Nếu x 1 ; x 2 là hai nghiệm của phương trình thì x 1 + x 2 = − b a x 1 . x 2 = c a
Đáp án: A
Đúng 0
Bình luận (0)
Cho phương trình a x 2 + b x + c = 0 a ≠ 0 thỏa mãn 2a + 6b + 19c = 0. Chứng minh phương trình có nghiệm trong 0 ; 1 3
Cho phuong trình bậc hai ax2 + bx+ c =0 có hai nghiệm x1,x2 deu khác 0 . Phương trình bậc hai nhận 2x1 và 2x2 làm nghiệm là:
x1+x2=-b/a; x1x2=c/a
=>2x1+2x2=-2b/a; 4x1x2=4c/a
=>PT cần tìm là x^2+2b/a*x+4c/a=0
Đúng 0
Bình luận (0)
Chọn phát biểu đúng. Phương trình
a
x
2
+
b
x
+
c
(
a
≠
0
)
có hai nghiệm
x
1
;
x
2
. Khi đó: A.
x
1
+
x...
Đọc tiếp
Chọn phát biểu đúng. Phương trình a x 2 + b x + c ( a ≠ 0 ) có hai nghiệm x 1 ; x 2 . Khi đó:
A. x 1 + x 2 = - b a x 1 . x 2 = c a
B. x 1 + x 2 = b a x 1 . x 2 = c a
C. x 1 + x 2 = - b a x 1 . x 2 = - c a
D. x 1 + x 2 = b a x 1 . x 2 = - c a
Đáp án A
Cho phương trình bậc hai a x 2 + b x + c ( a ≠ 0 ) .
Nếu x 1 ; x 2 là hai nghiệm của phương trình thì:
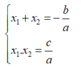
Đúng 0
Bình luận (0)
Cho tam thức bậc hai
f
x
a
x
2
+
b
x
+
c
,
a
,
b
,
c
∈
ℝ
,
a
≠
0
có hai nghiệm thực phân biệt
x
1
,...
Đọc tiếp
Cho tam thức bậc hai f x = a x 2 + b x + c , a , b , c ∈ ℝ , a ≠ 0 có hai nghiệm thực phân biệt x 1 , x 2 . Tính tích phân I = ∫ x 1 x 2 2 a x + b 3 . e a x 2 + b x + c d x
A. I = x 2 − x 1
B. I = x 2 − x 1 4
C. I = 0
D. I = x 2 − x 1 2
Cho phương trình ax^2 + bx + c = 0(a ≠ 0) có hai nghiệm phân biệt x1, x2
thoả mãn x1 =x2^2 . Chứng minh b^3 + a^2c + ac^2 = 3abc
Cho phương trình ax^2 + bx + c = 0(a ≠ 0) có hai nghiệm phân biệt x1, x2
thoả mãn x1 =x2^2 . Chứng minh b^3 + a^2c + ac^2 = 3abc .
xét các số thực a,b,c (a≠0) sao cho phương trình ax2+bx+c=0 có 2 nghiệm m, n thỏa mãn \(0\le m\le1;0\le m\le1\). tìm GTNN của \(Q=\dfrac{2a^2-ac-2ab+bc}{a^2-ab+ac}\)
\(Q=\dfrac{2-\dfrac{c}{a}-\dfrac{2b}{a}+\left(\dfrac{b}{a}\right)\left(\dfrac{c}{a}\right)}{1-\dfrac{b}{a}+\dfrac{c}{a}}=\dfrac{2-mn+2\left(m+n\right)-mn\left(m+n\right)}{1+m+n+mn}\)
\(Q=\dfrac{\left(2-mn\right)\left(m+n+1\right)}{\left(m+1\right)\left(n+1\right)}\ge\dfrac{\left[8-\left(m+n\right)^2\right]\left(m+n+1\right)}{\left(m+n+2\right)^2}\)
Đặt \(m+n=t\Rightarrow0\le t\le2\)
\(Q\ge\dfrac{\left(8-t^2\right)\left(t+1\right)}{\left(t+2\right)^2}-\dfrac{3}{4}+\dfrac{3}{4}=\dfrac{\left(2-t\right)\left(4t^2+15t+10\right)}{4\left(t+2\right)^2}+\dfrac{3}{4}\ge\dfrac{3}{4}\)
Dấu "=" xảy ra khi \(t=2\) hay \(m=n=1\)
Đúng 3
Bình luận (1)