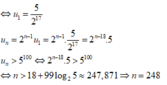Đáp án B.

Đặt  t = 2 + log   u 1 - 2 log   u 10 ≥ 0

⇔ 2 log   u 1 - 2 log   u 10 = t 2 - 2 , 

khi đó giả thiết trở thành:

log   u 1 - 2 log   u 10 + 2 + log   u 1 - 2 log   u 10 = 0

⇔ t 2 + t - 2 = 0  

<=> t = 1 hoặc t = -2

⇒ log   u 1 - 2 log   u 10 = - 1

⇔ log   u 1 + 1 = 2 log   u 10

⇔ log 10 u 1 = log u 10 2 ⇔ 10 u 1 = u 10 2   ( 1 )

Mà u_n+1 = 2u_n => u_n là cấp số nhân với công bội q = 2

=> u₁₀ = 2⁹ u₁ (2)

Từ (1), (2) suy ra

10 u 1 = 9 9 u 1 2 ⇔ 2 18 u 1 2 = 10 u 1 ⇔ u 1 = 10 2 18

⇒ u n = 2 n - 1 . 10 2 18 = 2 n . 10 2 19 .

Do đó  u n > 5 100 ⇔ 2 n . 10 2 19 > 5 100

⇔ n > log 2 5 100 . 2 19 10 = - log 2 10 + 100 log 2 5 + 19 ≈ 247 , 87

Vậy giá trị n nhỏ nhất thỏa mãn là n = 248.

Lời giải:

Ta có:

\(\log_2(x+4)+2\log_4(x+2)=2\log_{\frac{1}{2}}\frac{1}{8}=6\)

\(\Leftrightarrow 2\log_4(x+4)+2\log_4(x+2)=6\)

\(\Leftrightarrow \log_4(x+4)+\log_4(x+2)=3\)

\(\Leftrightarrow \log_4[(x+2)(x+4)]=3\)

\(\Leftrightarrow (x+2)(x+4)=4^3=64\)

\(\Leftrightarrow x^2+6x-56=0\)

\(\Leftrightarrow x=-3\pm \sqrt{65}\)

Kết hợp với ĐKXĐ ta suy ra \(x=-3+\sqrt{65}\) là nghiệm của pt

\(\dfrac{1}{2}\)log(x² + x - 5)=log(5x)+log(\(\dfrac{1}{5x}\))

⇔\(\sqrt{x^2+x-5}\) = 5x.\(\dfrac{1}{5x}\)

⇔x² + x - 5=1 ⇔ \(\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)

Kết hợp với ĐKXĐ của hàm nên chỉ có x=2 thoả mãn yêu cầu bài tập

potrzebuje pomocy tylko z początkiem, potem już sobie poradzę.

\(\log_{6^2}2-\frac{1}{2}\log_{\frac{1}{6}}3=\frac{1}{2}\log_62+\frac{1}{2}\log_63=\frac{1}{2}\log_6\left(2.3\right)=\frac{1}{2}\log_66=\frac{1}{2}\)

Tại sao log_6²2 - 1/2log_1/63 lại <=> 1/2log₆2 + 1/2 log_{63 ạ?}

đấy là công thứ tính nhé

\(\log_{a^{\alpha}}b=\frac{1}{\alpha}\log_ab\)

Lời giải:

ĐK: \(-2< x< 10\)

\(\log_3(10-x)+\frac{1}{2}\log_{\sqrt{3}}(x+2)=2\)

\(\Leftrightarrow \log_3(10-x)+\log_3(x+2)=2\)

\(\Leftrightarrow \log_3[(10-x)(x+2)]=2\)

\(\Leftrightarrow (10-x)(x+2)=9\)

\(\Leftrightarrow -x^2+8x+11=0\)

\(\Leftrightarrow x=4\pm 3\sqrt{3}\) (đều thỏa mãn đkxđ)

Vậy pt có nghiệm \(x=4\pm 3\sqrt{3}\)

a)     \({3^{{x^2} - 4x + 5}} = 9 \Leftrightarrow {x^2} - 4x + 5 = 2 \Leftrightarrow {x^2} - 4x + 3 = 0 \Leftrightarrow \left( {x - 3} \right)\left( {x - 1} \right) = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)

Vậy phương trình có nghiệm là \(x \in \left\{ {1;3} \right\}\)

b)    \(0,{5^{2x - 4}} = 4 \Leftrightarrow 2x - 4 = {\log _{0,5}}4 \Leftrightarrow 2x = 2 \Leftrightarrow x = 1\)

Vậy phương trình có nghiệm là x = 1

c)     \({\log _3}(2x - 1) = 3\)    ĐK: \(2x - 1 > 0 \Leftrightarrow x > \frac{1}{2}\)

\( \Leftrightarrow 2x - 1 = 27 \Leftrightarrow x = 14\) (TMĐK)

Vậy phương trình có nghiệm là x = 14

d)    \(\log x + \log (x - 3) = 1\)  ĐK: \(x - 3 > 0 \Leftrightarrow x > 3\)

\(\begin{array}{l} \Leftrightarrow \log \left( {x.\left( {x - 3} \right)} \right) = 1\\ \Leftrightarrow {x^2} - 3x = 10\\ \Leftrightarrow {x^2} - 3x - 10 = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {x - 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x =  - 2 (loại) \,\,\,\\x = 5 (TMĐK) \,\,\,\,\,\,\,\end{array} \right.\end{array}\)

Vậy phương trình có nghiệm x = 5