Gọi (I;r) là đường tròn nội tiếp \(\Delta ABC\) vuông tại A đường cao AH biết AB = 20cm, AC = 15cm.
a, Tính bán kính r.
b, Tính khoảng cách từ I đến AH
Những câu hỏi liên quan
Lam gọi Hùng bằng em, Hùng gọi Duơng bằng chú, Duơng gọi Bảo bằng bố , Bảo gọi Duy bằng bác , Duy gọi Kiên bằng cậu , Kiên gọi Thành là anh , Thành lại gọi Hải bằng ông
Hỏi Hùng gọi hải bằng j ?
Xem thêm câu trả lời
A gọi B là mẹ , B gọi C là bà ,C gọi D là dì,D gọi E là cụ ,E gọi G là bác,
G gọi H là ông ,H gọi I là kị,I gọi K là chú . Hỏi A gọi K bằng gì ?
Giúp mình nha !
Câu trả lời
A gọi K bằng mồm
Chúc bn hok tốt
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 1:Cho hbh ABCD . Gọi E,F,I là TĐ của AD,CB,CD . Gọi M là điểm đối xứng của I qua E a)Cm : AIDN là hbhb) Gọi N là điểm đối xứng của I qua F . Cm: BICN là hbhc)Gọi H là TĐ của AB . Cm: H là TĐ của MNBài 2:Cho hcn ABCD có AB4cm,AD3cm . Gọi E là TĐ của AD . Vẽ EF vuông góc CD tại Fa)Cm:AEFD và BCFE là hcnb)EF cắt BD tại H . Gọi I là TĐ của ADCm:DHEI là hbhc)AIHE là hình gì ? Vì sao ?d)Tính diện tích các hình sau : ABCD,ABD,AIHE,IEC ...
Đọc tiếp
Bài 1:Cho hbh ABCD . Gọi E,F,I là TĐ của AD,CB,CD . Gọi M là điểm đối xứng của I qua E
a)Cm : AIDN là hbh
b) Gọi N là điểm đối xứng của I qua F . Cm: BICN là hbh
c)Gọi H là TĐ của AB . Cm: H là TĐ của MN
Bài 2:Cho hcn ABCD có AB=4cm,AD=3cm . Gọi E là TĐ của AD . Vẽ EF vuông góc CD tại F
a)Cm:AEFD và BCFE là hcn
b)EF cắt BD tại H . Gọi I là TĐ của AD
Cm:DHEI là hbh
c)AIHE là hình gì ? Vì sao ?
d)Tính diện tích các hình sau : ABCD,ABD,AIHE,IEC
~Hết~
Giải giúp mk nhé ! Mk đang cần
C.ơn
Bài 1
a/ AB // DI
Mà AM thuộc tia AB => AM // DI (1)
=> Tứ giác AIDM là hình thang
E là trung điểm của AD (gt) => ED = EA
Xét △EDI và △EAM có:
- Góc DEI = Góc AEM (đối đỉnh)
- ED = EA (cmt)
- Góc EDI = Góc EAM (slt)
=> △EDI = △EAM (g.c.g)
=> AM = DI (2)
Từ (1) và (2). Vậy: Tứ giác AIDM là hình bình hành (đpcm)
b/ Chứng minh tương tự câu a
c/ Hình bình hành BICN có: BN = IC = CD/2 (I là trung điểm của CD)
Hình bình hành AIDM có: MA = ID = CD/2 (I là trung điểm của CD)
=> BN = MA (3)
Mặt khác ta có: H là trung điểm của AB (gt) hay HA = HB (4)
Từ (3) và (4) suy ra: BN + HA = HB + MA
Hay: HM = HN
Hay: H là trung điểm của MN (đpcm
Bài 2: Đề sai nên không thể giải
Đúng 1
Bình luận (3)
Cho ▲ABC vuông cân tại A gọi I là trung điểm của BC . Gọi M,N lần lượt là hình chiếu của I nên AB,AC
a) Chúng minh AMIN là hình vuông
b) Chứng minh MN//BC
c) Gọi E đối xứng vs I qua M ? t/g AEMN là hình gì
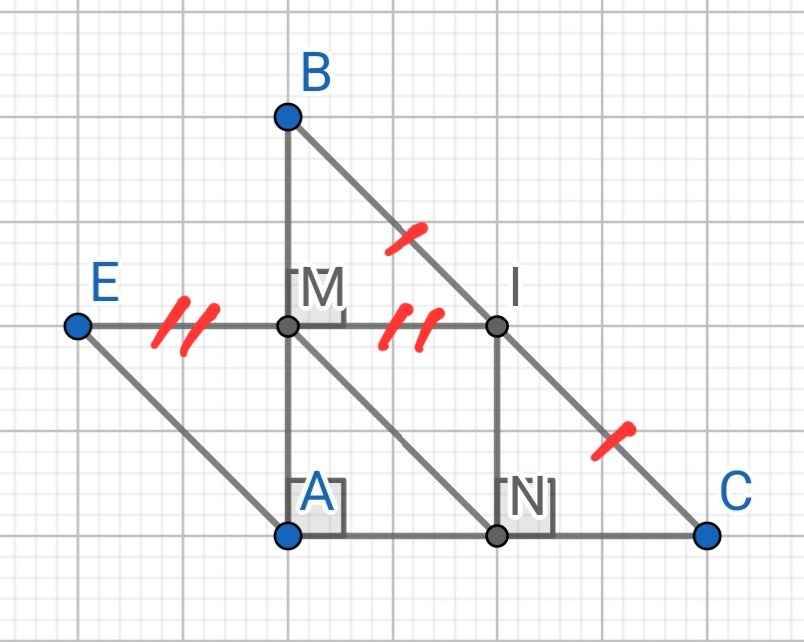
a) Do IM ⊥ AB (gt)
⇒ IM //AC
Mà I là trung điểm BC
⇒ M là trung điểm AB
⇒ IM là đường trung bình của ∆ABC
⇒ IM = AC/2
Do IN ⊥ AC (gt)
IN // AB
Mà I là trung điểm BC
⇒ N là trung điểm AC
⇒ AN = AC/2
⇒ IM = AC/2 = AN
Do IM // AC
⇒ IM // AN
Do M là trung điểm AB (cmt)
⇒ AM = IM = AB/2
Xét tứ giác AMIN có:
IM // AN (cmt)
IM = AN (cmt)
⇒ AMIN là hình bình hành
Mà ∠MAN = 90⁰ (∆ABC vuông tại A)
⇒ AMIN là hình chữ nhật
Lại có AM = IM (cmt)
⇒ AMIN là hình vuông
b) Do M là trung điểm AB (cmt)
N là trung điểm AC (cmt)
⇒ MN là đường trung bình của ∆ABC
⇒ MN // BC
c) Do E đối xứng với I qua M (gt)
⇒ ME = IM
⇒ ME = AN
Do IM // AN (cmt)
⇒ ME // AN
Xét tứ giác AEMN có:
ME // AN (cmt)
ME = AN (cmt)
⇒ AEMN là hình bình hành
Đúng 3
Bình luận (0)
chị ơi em chx học đường trung bình
Đúng 0
Bình luận (0)
cho đường tròn tâm O đường kính AB=8cm. Gọi I là trung điểm OB. Vẽ dây EF vuông góc AB tại I. Gọi D là điểm đối xứn của A qua I. Tính diện tích AEDF
IB=8/4=2cm
=>IA=6cm
=>AD=2*6=12cm
EI=căn AI*IB=2*căn 3(cm)
=>EF=4*căn 3(cm)
Xét tứ giác AEDF có
I là trung điểm chung của EF và AD
EF vuông góc AD
=>AEDF là hình thoi
=>S AEDF=1/2*AD*EF=1/2*4*căn 3*12=24*căn 3(cm2)
Đúng 2
Bình luận (1)
Gọi I là trung điểm của đoạn HK. Gọi A là điểm nằm giữa I và H
Chứng minh: AI = ( AK - AH ) :2
Lịch Sử 8 ~
Bài 6 : Các nước Anh, Pháp, Đức, Mĩ cuối thế kỉ XIX- đầu thế kỉ XX thường được gọi là gì ???
Vì sao lại gọi như vậy ???
Tham khảo nhé bạn:
Tên gọi cuối thế kỉ XĨ đầu thế kỉ XX là:
Anh: Chủ nghĩa đế quốc thực dân
Pháp: Chủ nghĩa đế quốc cho vay lãi
Đức:Chủ nghĩ quân phiệt hiếu chiến
Mĩ: chủ nghĩa đế quốc Các-tơ-rốt
Đúng 0
Bình luận (0)
cho lăng trụ abc.a'b'c'. Gọi I, I' là trọng tâm tam giác ABC, A'B'C'. Gọi O là trung điểm II'. Gọi g là trong tâm tứ diện ABCC', M là trung điểm A'B'. Chứng minh : O, M, G thẳng hàng
Cho ▲ABC vuông cân tại A gọi I là trung điểm của BC . Gọi M,N lần lượt là hình chiếu của I nên AB,AC
b) Chứng minh MN//BC
Dựa và ý a)
Có \(\dfrac{IM}{AC}=\dfrac{BI}{BC}=\dfrac{1}{2}\) ( định lý thales )
mà IM // AC ( cùng vuông góc với AB )
\(\Rightarrow\) IM là đường trung bình của tam giác ABC mà I là trung điểm của BC
\(\Rightarrow\) M là trung điểm của AB
Lại có \(\dfrac{IN}{AB}=\dfrac{IC}{CB}=\dfrac{1}{2}\) ( đly thales )
mà IN // AB ( cùng vuông góc với AC )
\(\Rightarrow\) IN là đường tb của tam giác ABC
mà I là trung điểm của BC nên N là trung điểm của AC
Có M và N lần lượt là trung điểm của AB và AC
\(\Rightarrow\) MN là đường trung bình của tam giác ABC
Suy ra MN // BC
Đúng 1
Bình luận (1)
hình bạn tự vẽ nhé:
ta có: AI=BI(tính chất đừng trung tuyến trong tg vuông)
=>tg AIB cân tại I
=>góc IAB= góc IBA (1)
ta lại có :
góc IAB=góc NMA(tính chất 2 đ chéo trong hcn) (2)
từ (1) (2) suy ra góc NMA=góc IBA
mà 2 góc này ở vị trí đồng vị
suy ra MN//BC
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC có đường truyến BD và CE cắt nhau tại G. Gọi I, K là trung điểm GB, GC. Chứng minh DE// IK và DE = IK.
Bài 2: Cho tam giác ABC có đường trung tuyến BD và CE. Gọi M, N là trung điểm BE, CD. Gọi MN cắt BD tại I và MN cắt CE tại I. Chứng minh MI = IK = KN.
Bài 1:
Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC
Suy ra: DE//BC và \(DE=\dfrac{BC}{2}\left(1\right)\)
Xét ΔGBC có
I là trung điểm của GB
K là trung điểm của GC
Do đó: IK là đường trung bình của ΔGBC
Suy ra: IK//BC và \(IK=\dfrac{BC}{2}\left(2\right)\)
Từ (1) và (2) suy ra DE//IK và DE=IK
Đúng 0
Bình luận (0)