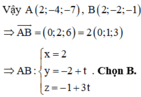Cho đường thẳng d : 2x + y -4 = 0 và A(4;1), B(1;-6). Tìm điểm M thuộc d thỏa mãn MA + MB nhỏ nhất

Những câu hỏi liên quan
Câu 26. Cho hai đường tròn (C):(x-2)^ 2 +(y-2)^ 2 =9;(C' ):x^ 2 +y^ 2 +4x-8y+11=0 ,biết (C) và (C') đối xứng nhau qua đường thẳng (a) .Phương trình của (a) là : A. 2x + 2y - 4 = 0 B.2x-y+3=0 . C. x + y - 4 = 0 . D. 2x + 2y = 0 .
Cho đường tròn (C):
x
2
+
y
2
- 2x + 6y + 8 0 và đường thẳng d: x + y + 4 0. Phương trình tiếp tuyến của đường tròn (C) và song song với đường thẳng d là: A.
x
+
y
-
4
0
B.
[
x
+
y
0...
Đọc tiếp
Cho đường tròn (C): x 2 + y 2 - 2x + 6y + 8 = 0 và đường thẳng d: x + y + 4 = 0. Phương trình tiếp tuyến của đường tròn (C) và song song với đường thẳng d là:
A. x + y - 4 = 0
B. [ x + y = 0 x + y + 4 = 0
C. x + y = 0
D. x + y - 2 = 0
Đáp án: B
(C): x 2 + y 2 - 2x + 6y + 8 = 0
⇔ (x - 1 ) 2 + (y + 3 ) 2 = 2 có I(1;-3), R = 2
Gọi d’ là tiếp tuyến của đường tròn (C) và song song với d
Vì d'//d ⇒ d': x + y + c = 0, (c ≠ 4)
d’ là tiếp tuyến của (C) nên d(I;d') = R
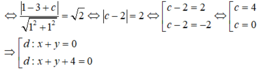
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ cho hai điểm B(4; 0) và C(-1; 4).a) Viết phương trình đường thẳng (d) đi qua điểm C và song song với đường thẳng y 2x-3. Xác định tọa độ giao điểm A của đường thẳng (d) với trục hoành Ox. b) Xác định các hệ số a và b biết đồ thị hàm số y ax +b đi qua 2 điểm B và C. Tính góc tạo bởi đường thẳng BC và trục hoành Ox (làm tròn đến phút).c) Tính chu vi của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét) (kết quả làm tròn đến chữ số thập phân thứ n...
Đọc tiếp
Trên mặt phẳng tọa độ cho hai điểm B(4; 0) và C(-1; 4).
a) Viết phương trình đường thẳng (d) đi qua điểm C và song song với đường thẳng y = 2x-3. Xác định tọa độ giao điểm A của đường thẳng (d) với trục hoành Ox.
b) Xác định các hệ số a và b biết đồ thị hàm số y= ax +b đi qua 2 điểm B và C. Tính góc tạo bởi đường thẳng BC và trục hoành Ox (làm tròn đến phút).
c) Tính chu vi của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét) (kết quả làm tròn đến chữ số thập phân thứ nhất).
a) Gọi (d): y=ax+b
Vì (d)//y=2x-3 nên \(\left\{{}\begin{matrix}a=2\\b\ne-3\end{matrix}\right.\)
Vậy: (d): y=2x+b
Vì (d) đi qua điểm C(-1;4) nên
Thay x=-1 và y=4 vào (d), ta được:
\(2\cdot\left(-1\right)+b=4\)
hay b=6
Vậy: (d): y=2x+6
Thay y=0 vào (d), ta được:
2x+6=0
hay x=-3
Vậy: A(-3;0)
b) Vì y=ax+b đi qua hai điểm B(4;0) và C(-1;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}4a+b=0\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5a=-4\\b=a+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{4}{5}\\b=\dfrac{-4}{5}+4=\dfrac{-4}{5}+\dfrac{20}{5}=\dfrac{16}{5}\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Trên mặt phẳng tọa độ cho hai điểm B(4; 0) và C(-1; 4). a) Viết phương trình đường thẳng (d) đi qua điểm C và song song với đường thẳng y 2x-3. Xác định tọa độ giao điểm A của đường thẳng (d) với trục hoành Ox. b) Xác định các hệ số a và b biết đồ thị hàm số y ax +b đi qua 2 điểm B và C. Tính góc tạo bởi đường thẳng BC và trục hoành Ox (làm tròn đến phút). c) Tính chu vi của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét) (kết quả làm tròn đến chữ số thập phân thứ...
Đọc tiếp
Trên mặt phẳng tọa độ cho hai điểm B(4; 0) và C(-1; 4).
a) Viết phương trình đường thẳng (d) đi qua điểm C và song song với đường thẳng y = 2x-3. Xác định tọa độ giao điểm A của đường thẳng (d) với trục hoành Ox.
b) Xác định các hệ số a và b biết đồ thị hàm số y= ax +b đi qua 2 điểm B và C. Tính góc tạo bởi đường thẳng BC và trục hoành Ox (làm tròn đến phút).
c) Tính chu vi của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét) (kết quả làm tròn đến chữ số thập phân thứ nhất).
a) Gọi (d): y=ax+b
Vì (d)//y=2x-3 nên ta có: \(\left\{{}\begin{matrix}a=2\\b\ne-3\end{matrix}\right.\)
=> (d): y=2x+b
Thay x=-1 và y=4 vào (d), ta được:
\(2\cdot\left(-1\right)+b=4\)
\(\Leftrightarrow b=6\)
Vậy: (D): y=2x+6
Thay y=0 vào (d),ta được:
\(2x+6=0\)
\(\Leftrightarrow x=-3\)
Vậy: A(-3;0)
b) Vì đồ thị hàm số y=ax+b đi qua hai điểm B(4;0) và C(-1;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}4a+b=0\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5a=-4\\-a+b=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{4}{5}\\b=4+a=4+\dfrac{-4}{5}=4-\dfrac{4}{5}=\dfrac{16}{5}\end{matrix}\right.\)
Vậy: \(a=-\dfrac{4}{5}\); \(b=\dfrac{16}{5}\)
c) Độ dài đoạn thẳng AB là:
\(AB=\sqrt{\left(-3-4\right)^2+\left(0-0\right)^2}=7\)(cm)
Độ dài đoạn thẳng AC là:
\(AC=\sqrt{\left(-3+1\right)^2+\left(0-4\right)^2}=2\sqrt{5}\left(cm\right)\)
Độ dài đoạn thẳng BC là:
\(BC=\sqrt{\left(4+1\right)^2+\left(0-4\right)^2}=\sqrt{41}\left(cm\right)\)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC\)
\(=7+2\sqrt{5}+\sqrt{41}\)
\(\simeq17,9\left(cm\right)\)
Đúng 1
Bình luận (1)
Câu 26: Đường thẳng y -x + 5 cắt trục hoành tại điểm nào?A. (-5; 0) B. (1; 0) C. (5; 0) D. (1; 4)Câu 27: Đường thẳng y 2x – 1 cắt trục tung tại điểm nào?A. (0; -1) B. (0; 1) C. (1/2;0) D. (-1; 0)Câu 28: Đường thẳng y 3x + 2 và đường thẳng y -x + 6 cắt nhau tại điểm:A. (1; 5) B . (2; 7) C. (2; 4) D. (4; 14).Câu 29: Điểm thuộc đường thẳng y 4x - 2 là:A. (0; 2) B . (3; 1) C. (2; 6) D. (1; 6).Câu 30: Đồ thị của hàm số y 2x + 3 là đường thẳng đi qua hai điểm ph...
Đọc tiếp
Câu 26: Đường thẳng y = -x + 5 cắt trục hoành tại điểm nào?
A. (-5; 0) B. (1; 0) C. (5; 0) D. (1; 4)
Câu 27: Đường thẳng y = 2x – 1 cắt trục tung tại điểm nào?
A. (0; -1) B. (0; 1) C. (1/2;0) D. (-1; 0)
Câu 28: Đường thẳng y = 3x + 2 và đường thẳng y = -x + 6 cắt nhau tại điểm:
A. (1; 5) B . (2; 7) C. (2; 4) D. (4; 14).
Câu 29: Điểm thuộc đường thẳng y = 4x - 2 là:
A. (0; 2) B . (3; 1) C. (2; 6) D. (1; 6).
Câu 30: Đồ thị của hàm số y = 2x + 3 là đường thẳng đi qua hai điểm phân biệt sau
A. (0; 3) và (3; 0) C. (0; 3) và (1,5; 2)
C. (0; 3) và (1; 5) D. (3; 0) và (1,5; 0)
Câu 31: Đồ thị của hàm số y = ax + b (a ≠ 0) là
một đường cong Parabol.
một đường thẳng đi qua hai điểm (0; b) và ((-b)/a;0)
một đường thẳng đi qua gốc toạ độ.
một đường thẳng đi qua hai điểm (b; 0) và (0; b)
Câu 32: Khẳng định nào về hàm số y = x + 3 là sai
A. Cắt Oy tại (0; 3) B. Nghịch biến trên
C. Cắt Ox tại (-3; 0) D. Đồng biến trên
Câu 33: Góc tạo bởi đường thẳng: y = với trục Ox bằng
A. 300 B . 300 C. 450 D. 600.
Trong mặt phẳng tọa độ Oxy cho điểm A(4; – 1), đường thẳng (d) : 3x – 2y + 1 = 0 và đường tròn (C) :
x^2 + y^2 - 2x + 4y -4 = 0
a. Tìm tọa độ A’ và phương trình (d’) lần lượt là ảnh của A và (d) qua phép tịnh tiến theo vectơ v = (– 2; 3)
b. Tìm phương trình đường tròn (C’) là ảnh của đường tròn (C) qua phép đối xứng trục là đường thẳng (D) : x – y = 0
Trong không gian Oxyz, cho đường thẳng
∆
:
x
2
y
+
1
-
3
z
+
4
-
3
và mặt phẳng
P
:
2
x
+
y...
Đọc tiếp
Trong không gian Oxyz, cho đường thẳng ∆ : x 2 = y + 1 - 3 = z + 4 - 3 và mặt phẳng P : 2 x + y - z - 3 = 0 . Đường thẳng d đi qua M 2 ; - 3 ; - 4 cắt ∆ và (P) lần lượt tại A, B sao cho M là trung điểm của AB có phương trình là
A. x = 2 t y = 2 - 3 t z = 6 - 4 t
B. x = 2 y = - 2 + t z = - 1 + 3 t
C x = 2 + 2 t y = 3 z = - 4 + 6 t
D. x = 2 y = - 3 + 2 t z = - 4 + 3 t
Cho điểm A(1;3) và đường thẳng d: 2x – 3y + 4 0. Số đường thẳng qua A và tạo với d một góc
60
°
là: A.0 B. 1 C.2 D.Vô số
Đọc tiếp
Cho điểm A(1;3) và đường thẳng d: 2x – 3y + 4 = 0. Số đường thẳng qua A và tạo với d một góc 60 ° là:
A.0
B. 1
C.2
D.Vô số
Đường thẳng d có VTPT n d → ( 2 ; − 3 )
Gọi đường thẳng ∆ thỏa mãn có VTPT n Δ → ( a ; b )
Vì góc giữa hai đường thẳng bằng 600 nên:
cos 60 0 = c os ( n d → ; n Δ → ) = 2 a − 3 b 2 2 + ( − 3 ) 2 . a 2 + b 2 ⇔ 1 2 = 2 a − 3 b 13 . a 2 + b 2 ⇔ 13 . a 2 + b 2 = 2. 2 a − 3 b ⇔ 13 ( a 2 + b 2 ) = 4 ( 4 a 2 − 12 a b + 9 b 2 ) ⇔ − 3 a 2 + 48 a b − 23 b 2 = 0 ⇔ − 3 a b 2 + 48. a b − 23 = 0 ( * )
Phương trình (*) có 2 nghiệm phân biệt. Ứng với mỗi nghiệm ta tìm được 1 cặp số (a, b) là VTPT của đường thẳng ∆. Từ đó, ta viết được 2 phương trình đường thẳng ∆ thỏa mãn.
ĐÁP ÁN C
Đúng 0
Bình luận (0)
Cho đường tròn ( C) : x^2 + y^2 - 2x + 4y - 4 = 0, có tâm I và đường thẳng d : √2x + my + 1 - √2 = 0
a) Tìm m để đường thẳng cắt đường tròn (C) tại hai điểm phân biệt A, B
b) Tìm m để diện tích tam giác IAB là lớn nhất
Đường tròn (C) tâm \(I\left(1;-2\right)\) bán kính \(R=3\)
a. Đường thẳng cắt đường tròn tại 2 điểm pb khi:
\(d\left(I;d\right)< R\Leftrightarrow\dfrac{\left|\sqrt{2}-2m+1-\sqrt{2}\right|}{\sqrt{2+m^2}}< 3\)
\(\Leftrightarrow\left(2m-1\right)^2< 9\left(m^2+2\right)\)
\(\Leftrightarrow8m^2+4m+17>0\) (luôn đúng)
Vậy đường thẳng luôn cắt đường tròn tại 2 điểm pb với mọi m
b. \(S_{IAB}=\dfrac{1}{2}IA.IB.sin\widehat{AIB}=\dfrac{1}{2}R^2.sin\widehat{AIB}\le\dfrac{1}{2}R^2\) do \(sin\widehat{AIB}\le1\)
Dấu "=" xảy ra khi \(sin\widehat{AIB}=1\Rightarrow\Delta IAB\) vuông cân tại I
\(\Rightarrow d\left(I;d\right)=\dfrac{R}{\sqrt{2}}\Leftrightarrow\dfrac{\left|2m-1\right|}{\sqrt{m^2+2}}=\dfrac{3}{\sqrt{2}}\)
\(\Leftrightarrow m^2+8m+16=0\Rightarrow m=-4\)
Đúng 0
Bình luận (1)