Các câu hỏi tương tự
Cho đường thẳng d: x-y +6=0 và hai điểm A(2;2) B(3;0). Tìm điểm M thuộc d sao cho MA + MB nhỏ nhất.
Cho ba điểm A( -6;3) ;B( 0; -1) và C( 3;2). Tìm điểm M trên đường thẳng d : 2x- y + 3 0 mà
M
A
→
+
M
B
→
+
M
C
→
nhỏ nhất là:
Đọc tiếp
Cho ba điểm A( -6;3) ;B( 0; -1) và C( 3;2). Tìm điểm M trên đường thẳng d : 2x- y + 3= 0 mà M A → + M B → + M C → nhỏ nhất là:
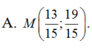
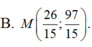
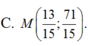
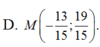
Cho 2 điểm A(3; 4), B(1; 1) và đường thẳng d: x-y+1 = 0. Tìm M trên d sao cho: MA + MB nhỏ nhất.
Xem chi tiết
Cho A(0;2), B(2;-2) và d:x - y - 1=0. Điểm M thuộc d thỏa mãn MA+MB nhỉ nhất khi
Cho tam giác ABC và đường thẳng d a) tìm điểm I để Vecto IA+IB+3IC =vecto 0. b) Tìm trên d điểm M sao cho |Vecto MA+MB+3MC| nhỏ nhất giúp mk với mk đang cần gấp !!!
Cho đường tròn (C): x^2 + y^2 +10x-8y+1=0 và d:-x+y-5=0
a) Qua điểm M thuộc d kẻ tiếp tuyến MA,MB
Tìm M sao cho diện tích tam giác IAB lớn nhất (I là tâm đường tròn)
b) Tim P thuộc d sao cho diện tích PAI=3, A tiếp điểm các tiếp tuyến từ P.
cho tam giác ABC đều có cạnh bằng a .tìm điểm M thuộc đường thẳng d đi qua BC để biểu thức T=|MA+MB+MC| đạt giá trị nhỏ nhất và tính GTNN đó
Xem chi tiết
cho tam giác ABC đều có cạnh bằng a .tìm điểm M thuộc đường thẳng d đi qua BC để biểu thức T=|MA+MB+MC| đạt giá trị nhỏ nhất và tính GTNN đó
Xem chi tiết
Cho A(0;-3) , B(1;3) và đt d: 2x-y-3=0 . Tìm toạ độ điểm M trên d sao cho AM+MB là nhỏ nhất.









