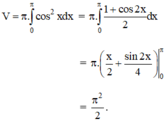Tính S hình phẳng giới hạn bởi y=cos^2x,Ox,Oy,x=pi

Những câu hỏi liên quan
cho hình phẳng h được giới hạn bởi đồ thị hàm số y = e mũ 2x trục Ox Oy và đường thẳng x = 2 tính s hình phẳng trên
Tham khảo:
Do \(ex>0;∀xex>0;∀x\)
Diện tích hình phẳng:
\(S=2∫0exdx=ex|20=e2−1\)
Đúng 0
Bình luận (0)
Biết diện tích hình phẳng giới hạn bởi đường cong yf(x), y0, x2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong yf(2x), trục hoành Ox và hai đường thẳng x0, xa bằng:
Đọc tiếp
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x), y=0, x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0, x=a bằng:
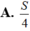
![]()
![]()
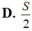
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x),y=0,x=0,x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0,x=a bằng
A. S/4.
B. 4S.
C. 2S.
D. S/2.
Tính thể tích khối tròn xoay đó hình phẳng giới hạn bởi các đường sau quay quanh Ox:
y = cos x;y = 0; x = π
Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường thẳng
y
cos
x
,
y
0
,
x
0
,
x
π
quay quanh trục Ox. A.
π
3
B.
π
2
2
C.
π
2
D. ...
Đọc tiếp
Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường thẳng y = cos x , y = 0 , x = 0 , x = π quay quanh trục Ox.
A. π 3
B. π 2 2
C. π 2
D. π 2 3
Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh trục Ox :
a) \(y=1-x^2;y=0\)
b) \(y=\cos x;y=0;x=0;x=\pi\)
c) \(y=\tan x;y=0;x=0;x=\dfrac{\pi}{4}\)
a) Phương trình hoành độ giao điểm
1 - x2 = 0 ⇔ x = ±1.
Thể tích cần tìm là :
b) Thể tích cần tìm là :
c) Thể tích cần tìm là :
.
Đúng 0
Bình luận (0)
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
y
x
+
1
x
-
2
và các trục tọa độ Ox, Oy ta được: S
a
ln
b
c
-
1
. Biết a nguyên dương . Chọn đáp án đúng A . a + b + c 8 B . a b C . a – b + c 1 D . a + 2b – 9 c
Đọc tiếp
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm
số y = x + 1 x - 2 và các trục tọa độ Ox, Oy ta được: S=
a ln b c - 1 . Biết a nguyên dương . Chọn đáp án đúng
A . a + b + c = 8
B . a > b
C . a – b + c = 1
D . a + 2b – 9 = c
Hình (S) giới hạn bởi
y
3
x
+
2
,
O
x
,
O
y
.
Tính thể tích khối tròn xoay khi quay hình (S) quanh trục Ox. A.
8
π
3
B.
4
π
3
C.
8...
Đọc tiếp
Hình (S) giới hạn bởi y = 3 x + 2 , O x , O y . Tính thể tích khối tròn xoay khi quay hình (S) quanh trục Ox.
A. 8 π 3
B. 4 π 3
C. 8 π 9
D. 16 π 3
Chọn C.
Phương trình hoành độ giao điểm:
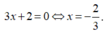
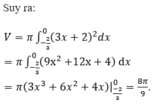
Đúng 0
Bình luận (0)
Hình phẳng S giới hạn bởi ba đường y x; y 2 - x; x 0. Khi quay S quanh Ox, Oy tương ứng ta được hai vật thể tròn xoay có thể tích là
V
x
;
V
y
. Hãy lựa chọn phương án đúng? A.
V
y
π
3
B.
V
x
12 C.
V
x
+...
Đọc tiếp
Hình phẳng S giới hạn bởi ba đường y = x; y = 2 - x; x = 0. Khi quay S quanh Ox, Oy tương ứng ta được hai vật thể tròn xoay có thể tích là V x ; V y . Hãy lựa chọn phương án đúng?
A. V y = π 3
B. V x = 12
C. V x + V y = 20 π 3
D. V x + V y = 8 π 3
Ta có:
V y = 2 . 1 3 πr 2 h = 2 π 3 V x = 1 3 πh R 2 + r 2 + Rr - r 2 = 1 3 π . 1 4 + 2 . 1 = 2 π
Do đó V x + V y = 8 π 3
Đáp án D
Đúng 0
Bình luận (0)