a. 4cosx.sin²x = cosx-sinx
b. sinx.sin4x=2cosx(π/6-x)√3cosx.sin2x
Những câu hỏi liên quan
Phương trình (sinx - cosx)(sinx + 2cosx - 3) 0 có tất cả bao nhiêu nghiệm thực thuộc khoảng
-
3
π
4
;
π
? A. 3 B. 0. C. 1. D. 2.
Đọc tiếp
Phương trình (sinx - cosx)(sinx + 2cosx - 3) = 0 có tất cả bao nhiêu nghiệm thực thuộc khoảng - 3 π 4 ; π ?
A. 3
B. 0.
C. 1.
D. 2.
Giải pt
\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)
\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)
\(sin2x-cos2x+3sinx-cosx-1=0\)
1.
\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)
\(\Leftrightarrow\sqrt{3}sinx+cosx+sinx+2cosx=3\)
\(\Leftrightarrow\left(\sqrt{3}+1\right)sinx+3cosx=3\)
\(\Leftrightarrow\sqrt{13+2\sqrt{3}}\left[\dfrac{\sqrt{3}+1}{\sqrt{13+2\sqrt{3}}}sinx+\dfrac{3}{\sqrt{13+2\sqrt{3}}}cosx\right]=3\)
Đặt \(\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)
\(pt\Leftrightarrow\sqrt{13+2\sqrt{3}}sin\left(x+\alpha\right)=3\)
\(\Leftrightarrow sin\left(x+\alpha\right)=\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\\x+\alpha=\pi-arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)
Vậy phương trình đã cho có nghiệm:
\(x=k2\pi;x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\)
Đúng 0
Bình luận (0)
2.
\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)
\(\Leftrightarrow2sinx.cos^2x+cos2x.cosx+2cos2x-sinx=0\)
\(\Leftrightarrow\left(2cos^2x-1\right)sinx+cos2x.cosx+2cos2x=0\)
\(\Leftrightarrow cos2x.sinx+cos2x.cosx+2cos2x=0\)
\(\Leftrightarrow cos2x.\left(sinx+cosx+2\right)=0\)
\(\Leftrightarrow cos2x=0\)
\(\Leftrightarrow2x=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Vậy phương trình đã cho có nghiệm \(x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Đúng 0
Bình luận (0)
III. Phương trình bậc nhất đối với sinx và cosx:*Giải các phương trình bậc nhất đối với sinx và cosx sau đây:(2.1)1) 2sinx-2cosxsqrt{2}2) cosx-sqrt{3}sinx13) sqrt{3}sindfrac{x}{3}+cosdfrac{x}{2}sqrt{2}4) cosx-sinx15) 2cosx+2sinxsqrt{6}6) sin3x+sqrt{3}cosxsqrt{2}7) 3sinx-2cosx2(2.3)1) left(sinx-1right)left(1+cosxright)cos^2x2) sinleft(dfrac{pi}{2}+2xright)+sqrt{3}sinleft(pi-2xright)13) sqrt{2}left(cos^4x-sin^4xright)cosx+sinx4) sin2x+cos2xsqrt{2}sin3x5) sinxsqrt{2}sin5x-cosx6) sin8x-cos6xsqrt{3}l...
Đọc tiếp
III. Phương trình bậc nhất đối với sinx và cosx:
*Giải các phương trình bậc nhất đối với sinx và cosx sau đây:
(2.1)
1) \(2sinx-2cosx=\sqrt{2}\)
2) \(cosx-\sqrt{3}sinx=1\)
3) \(\sqrt{3}sin\dfrac{x}{3}+cos\dfrac{x}{2}=\sqrt{2}\)
4) \(cosx-sinx=1\)
5) \(2cosx+2sinx=\sqrt{6}\)
6) \(sin3x+\sqrt{3}cosx=\sqrt{2}\)
7) \(3sinx-2cosx=2\)
(2.3)
1) \(\left(sinx-1\right)\left(1+cosx\right)=cos^2x\)
2) \(sin\left(\dfrac{\pi}{2}+2x\right)+\sqrt{3}sin\left(\pi-2x\right)=1\)
3) \(\sqrt{2}\left(cos^4x-sin^4x\right)=cosx+sinx\)
4) \(sin2x+cos2x=\sqrt{2}sin3x\)
5) \(sinx=\sqrt{2}sin5x-cosx\)
6) \(sin8x-cos6x=\sqrt{3}\left(sin6x+cos8x\right)\)
7) \(cos3x-sinx=\sqrt{3}\left(cosx-sin3x\right)\)
8) \(2sin^2x+\sqrt{3}sin2x=3\)
9) \(sin^4x+cos^4\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{4}\)
(2.3)
1) \(\dfrac{\sqrt{3}\left(1-cos2x\right)}{2sinx}=cosx\)
2) \(cotx-tanx=\dfrac{cosx-sinx}{sinx.cosx}\)
3) \(\dfrac{\sqrt{3}}{cosx}+\dfrac{1}{sinx}=4\)
4) \(\dfrac{1+sinx}{1+cosx}=\dfrac{1}{2}\)
5) \(3cosx+4sinx+\dfrac{6}{3cosx+4sinx+1}=6\)
(2.4)
a) Tìm nghiệm \(x\in\left(\dfrac{2\pi}{5};\dfrac{6\pi}{7}\right)\) của phương trình \(cos7x-\sqrt{3}sin7x+\sqrt{2}=0\)
b) Tìm nghiệm \(x\in\left(0;\pi\right)\) của phương trình \(4sin^2\dfrac{x}{2}-\sqrt{3}cos2x=1+2cos^2\left(x-\dfrac{3\pi}{4}\right)\)
(2.5) Xác định tham số m để các phương trình sau đây có nghiệm:
a) \(mcosx-\left(m+1\right)sinx=m\)
b) \(\left(2m-1\right)sinx+\left(m-1\right)cosx=m-3\)
(2.6) Tìm GTLN, GTNN (nếu có) của các hàm số sau đây:
a) \(y=3sinx-4cosx+5\)
b) \(y=cos2x+sin2x-1\)
2.1
a.
\(\Leftrightarrow sinx-cosx=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{4}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{12}+k2\pi\\x=\dfrac{13\pi}{12}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
b.
\(cosx-\sqrt{3}sinx=1\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
c.
\(\sqrt{3}sin\dfrac{x}{3}+cos\dfrac{x}{2}=\sqrt{2}\)
Câu này đề đúng không nhỉ? Nhìn thấy có vẻ không đúng lắm
d.
\(cosx-sinx=1\)
\(\Leftrightarrow\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=-\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?a) {y x + sinx, y x với 0
≤
x
≤
π
} và {y x + sinx, y x với
π
≤
x
≤
2
π
}b) {y sinx, y 0 với 0
≤
x
≤
π
} và {y cosx, y 0 với 0
≤
x
≤
π
};c) {y ...
Đọc tiếp
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?
a) {y = x + sinx, y = x với 0 ≤ x ≤ π } và {y = x + sinx, y = x với π ≤ x ≤ 2 π }
b) {y = sinx, y = 0 với 0 ≤ x ≤ π } và {y = cosx, y = 0 với 0 ≤ x ≤ π };
c) {y = x , y = x 2 }
và { y = 1 - x 2 , y = 1 − x}
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?a) {y x + sinx, y x với 0 ≤ x ≤ π} và {y x + sinx, y x với π ≤ x ≤ 2π}b) {y sinx, y 0 với 0 ≤ x ≤ π} và {y cosx, y 0 với 0 ≤ x ≤ π};c) {y √x, y
x
2
}và { , y 1 − x}
Đọc tiếp
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?
a) {y = x + sinx, y = x với 0 ≤ x ≤ π} và {y = x + sinx, y = x với π ≤ x ≤ 2π}
b) {y = sinx, y = 0 với 0 ≤ x ≤ π} và {y = cosx, y = 0 với 0 ≤ x ≤ π};
c) {y = √x, y = x 2 }
và {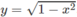 
, y = 1 − x}
1. sin^8(x) - cos^8(x) - 4sin^6(x) + 6sin^4(x) - 4sin^2(x) = 1
2. sin6x+sin4x+sin2x/1+cos2x+cos4x = 2sin2x
3. 1+sin2x /cosx+sinx - 1-tan^2(x/2)/1+tan^2(x/2) = sinx
4. cos4x + 4cos2x + 3 = 8cos^4(x)
5. 1+cosx+cos2x+cos3x/ 2cos^2(x)+cosx-1 = 2cosx
1. sin^8(x) - cos^8(x) - 4sin^6(x) + 6sin^4(x) - 4sin^2(x) = 1
2. sin6x+sin4x+sin2x/1+cos2x+cos4x = 2sin2x
3. 1+sin2x /cosx+sinx - 1-tan^2(x/2)/1+tan^2(x/2) = sinx
4. cos4x + 4cos2x + 3 = 8cos^4(x)
5. 1+cosx+cos2x+cos3x/ 2cos^2(x)+cosx-1 = 2cosx
\(sin^8x-cos^8x-4sin^6x+6sin^4x-4sin^2x\)
\(=sin^8x-\left(1-sin^2x\right)^4-4sin^6x+6sin^4x-4sin^2x\)
\(=sin^8x-\left(1-4sin^2x+6sin^4x-4sin^6x+sin^8x\right)-4sin^6x+6sin^4x-4sin^2x\)\(=-1\) (bạn chép nhầm đề)
b/ \(\frac{sin6x+sin2x+sin4x}{1+cos2x+cos4x}=\frac{2sin4x.cos2x+sin4x}{1+cos2x+2cos^22x-1}=\frac{sin4x\left(2cos2x+1\right)}{cos2x\left(2cos2x+1\right)}=\frac{sin4x}{cos2x}=\frac{2sin2x.cos2x}{cos2x}=2sin2x\)
c/ \(\frac{1+sin2x}{cosx+sinx}-\frac{1-tan^2\frac{x}{2}}{1+tan^2\frac{x}{2}}=\frac{sin^2x+cos^2x+2sinx.cosx}{cosx+sinx}-\left(1-tan^2\frac{x}{2}\right)cos^2\frac{x}{2}\)
\(=\frac{\left(sinx+cosx\right)^2}{sinx+cosx}-\left(cos^2\frac{x}{2}-sin^2\frac{x}{2}\right)=sinx+cosx-cosx=sinx\)
d/ \(cos4x+4cos2x+3=2cos^22x-1+4cos2x+3\)
\(=2\left(cos^22x+2cos2x+1\right)=2\left(cos2x+1\right)^2=2\left(2cos^2x-1+1\right)^2=8cos^4x\)
e/
Đúng 0
Bình luận (1)
Cho phương trình: cos2x+(1+2cosx)(sinx-cosx)=0. Số họ nghiệm của phương trình dạng x = a + k 2 π là:
A.4
B.2
C.1
D.3
1) sin^2left(frac{x}{2}-frac{pi}{4}right).tan^2x-cos^2frac{x}{2}0
2) tanxsin^2xleft(c-frac{pi}{2010}right)+cos^2left(2x+frac{pi}{2010}right)+sinx.sinleft(3x+frac{pi}{1005}right)
3) 1+2cosxleft(sinx-1right)+sqrt{2}sinx+4cosx.sin^2frac{x}{2}0
4) 3cos4x-8cos^6x+2cos4x3
5) 1+sinx.sin2x-cosx.sin^22x2cos^2left(frac{pi}{4}-xright)
6) sinx.sin4xsqrt{2}cosleft(frac{pi}{6}-xright)-4sqrt{3}cos^2x.sinx.cos2x
7) frac{tan^2x+tanx}{tan^2x+1}frac{sqrt{2}}{2}sinleft(x+frac{pi}{4}right)
8) cos^4x+sin^4x+co...
Đọc tiếp
1) \(sin^2\left(\frac{x}{2}-\frac{\pi}{4}\right).tan^2x-cos^2\frac{x}{2}=0\)
2) \(tanx=sin^2x\left(c-\frac{\pi}{2010}\right)+cos^2\left(2x+\frac{\pi}{2010}\right)+sinx.sin\left(3x+\frac{\pi}{1005}\right)\)
3) \(1+2cosx\left(sinx-1\right)+\sqrt{2}sinx+4cosx.sin^2\frac{x}{2}=0\)
4) \(3cos4x-8cos^6x+2cos4x=3\)
5) \(1+sinx.sin2x-cosx.sin^22x=2cos^2\left(\frac{\pi}{4}-x\right)\)
6) \(sinx.sin4x=\sqrt{2}cos\left(\frac{\pi}{6}-x\right)-4\sqrt{3}cos^2x.sinx.cos2x\)
7) \(\frac{tan^2x+tanx}{tan^2x+1}=\frac{\sqrt{2}}{2}sin\left(x+\frac{\pi}{4}\right)\)
8) \(cos^4x+sin^4x+cos\left(x-\frac{\pi}{4}\right).sin\left(3x-\frac{\pi}{4}\right)-\frac{3}{2}=0\)
Câu 2 bạn coi lại đề
3.
\(1+2sinx.cosx-2cosx+\sqrt{2}sinx+2cosx\left(1-cosx\right)=0\)
\(\Leftrightarrow sin2x-\left(2cos^2x-1\right)+\sqrt{2}sinx=0\)
\(\Leftrightarrow sin2x-cos2x=-\sqrt{2}sinx\)
\(\Leftrightarrow\sqrt{2}sin\left(2x-\frac{\pi}{4}\right)=\sqrt{2}sin\left(-x\right)\)
\(\Leftrightarrow sin\left(2x-\frac{\pi}{4}\right)=sin\left(-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{4}=-x+k2\pi\\2x-\frac{\pi}{4}=\pi+x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
4.
Bạn coi lại đề, xuất hiện 2 số hạng \(cos4x\) ở vế trái nên chắc là bạn ghi nhầm
5.
\(\Leftrightarrow sinx.sin2x-cosx.sin^22x=2cos^2\left(\frac{\pi}{4}-x\right)-1\)
\(\Leftrightarrow sinx.sin2x-cosx.sin^22x=cos\left(\frac{\pi}{2}-2x\right)\)
\(\Leftrightarrow sinx.sin2x-cosx.sin^22x=sin2x\)
\(\Leftrightarrow sin2x\left(sinx-cosx.sin2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\Leftrightarrow x=...\\sinx-cosx.sin2x-1=0\left(1\right)\end{matrix}\right.\)
Xét (1):
\(\Leftrightarrow sinx-1-2sinx.cos^2x=0\)
\(\Leftrightarrow sinx-1-2sinx\left(1-sin^2x\right)=0\)
\(\Leftrightarrow2sin^3x-sinx-1=0\)
\(\Leftrightarrow\left(sinx-1\right)\left(2sin^2x+2sinx+1\right)=0\)
\(\Leftrightarrow...\)
6.
\(sinx.sin4x=\sqrt{2}cos\left(\frac{\pi}{6}-x\right)-2\sqrt{3}cosx.sin2x.cos2x\)
\(\Leftrightarrow sinx.sin4x=\sqrt{2}cos\left(\frac{\pi}{6}-x\right)-\sqrt{3}cosx.sin4x\)
\(\Leftrightarrow sin4x\left(sinx+\sqrt{3}cosx\right)=\sqrt{2}sin\left(x+\frac{\pi}{3}\right)\)
\(\Leftrightarrow sin4x\left(\frac{1}{2}sinx+\frac{\sqrt{3}}{2}cosx\right)-\frac{\sqrt{2}}{2}sin\left(x+\frac{\pi}{3}\right)=0\)
\(\Leftrightarrow sin4x.sin\left(x+\frac{\pi}{3}\right)-\frac{\sqrt{2}}{2}sin\left(x+\frac{\pi}{3}\right)=0\)
\(\Leftrightarrow\left(sin4x-\frac{\sqrt{2}}{2}\right)sin\left(x+\frac{\pi}{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin4x=\frac{\sqrt{2}}{2}\\sin\left(x+\frac{\pi}{3}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow...\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời