Vẽ parabol
a. ( P ) : y = 3x^2 - 2x - 1
Vẽ các đường parabol sau:
a) \(y = {x^2} - 3x + 2\)
b) \(y = - 2{x^2} + 2x + 3\)
c) \(y = {x^2} + 2x + 1\)
d) \(y = - {x^2} + x - 1\)
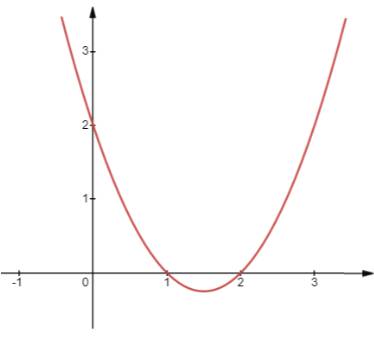
a) Đồ thị \(y = {x^2} - 3x + 2\)
- Có đỉnh là điểm \(I\left( {\frac{3}{2}; - \frac{1}{4}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{3}{2}\)
- \(a = 1 > 0\), quay bề lõm lên trên
- Đi qua điểm (0;2);(1;0)
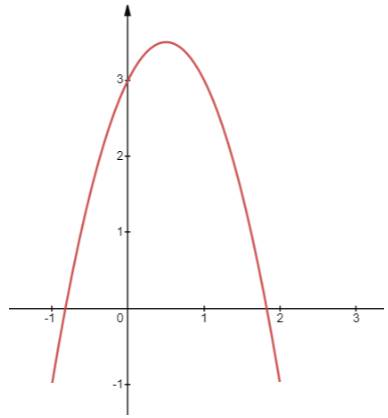
b) Đồ thị \(y = - 2{x^2} + 2x + 3\)
- Có đỉnh là điểm \(I\left( {\frac{1}{2};\frac{7}{2}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{1}{2}\)
- \(a = - 2 < 0\), quay bề lõm xuống dưới
- Đi qua điểm (0;3);(1;3)
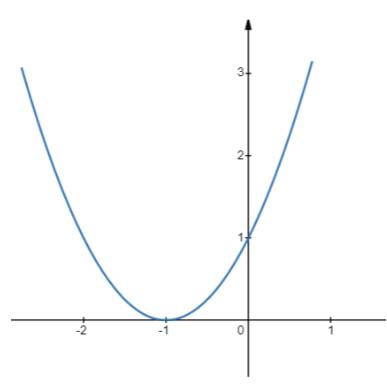
c) Đồ thị\(y = {x^2} + 2x + 1\)
- Có đỉnh là điểm \(I( - 1;0)\), có trục đối xứng là đường thẳng \(x = - 1\)
- \(a = 1 > 0\), quay bề lõm lên trên
- Đi qua điểm (0;1); (1;4)
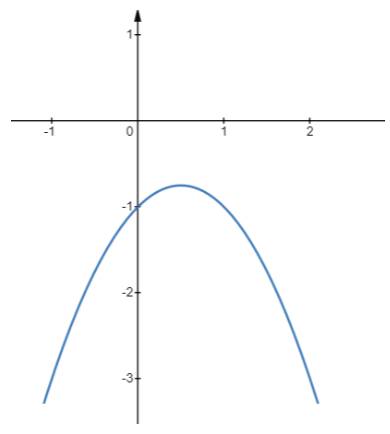
d) Đồ thị \(y = - {x^2} + x - 1\)
- Có đỉnh là điểm \(I\left( {\frac{1}{2};\frac{{ - 3}}{4}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{1}{2}\)
- \(a = - 1 < 0\), quay bề lõm xuống dưới
- Đi qua điểm (0;-1); (1;-1)
a) x2 - 2x - 3 = 0
Dễ thấy pt có a - b + c = 0 nên có hai nghiệm x1 = -1 ; x2 = 3
Vậy phương trình có hai nghiệm x1 = -1 ; x2 = 3
b) -x2 + 7x - 6 = 0
Dễ thấy pt có a + b + c = 0 nên có hai nghiệm x1 = 1 ; x2 = 6
Vậy phương trình có hai nghiệm x1 = 1 ; x2 = 6
*đths e chưa làm đc vì mới lớp 8 :v*
Cho parabol (P): y =1/3x2 và đường thẳng (đ): y =2x+m2-4m+3 (với m là tham số ).
a) Vẽ parabol (P) . b) Tìm m để đường thẳng (đ) đi qua gốc tọa độ O . c) Tìm toạ độ giao điểm của (đ) và (P) với m=1.
Cho parabol (P): \(y=2x^2\) và đường thẳng (d): y=2x+m (m là tham số). Vẽ parabol P.
Bài giải:
Cho parabol
và đường thẳng (m là tham số).
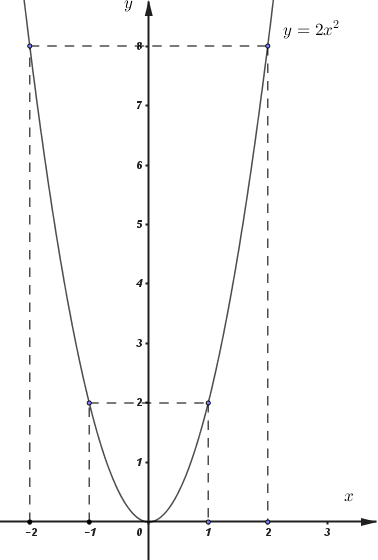
a) Vẽ parabol
Ta có bảng giá trị:
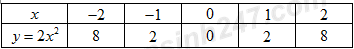
Vậy đồ thị hàm số là đường cong đi qua các điểm:
b) Với những giá trị nào của thì và chỉ có một điểm chung. Tìm tọa độ điểm chung đó.
Phương trình hoành độ giao điểm của hai đồ thị hàm số là:
Số giao điểm của đồ thị (P) và đường thẳng (d) cũng chính là số nghiệm của phương trình (*)
Đồ thị hàm số và chỉ có một điểm chung
b) Với những giá trị nào của
thì và chỉ có một điểm chung. Tìm tọa độ điểm chung đó.
Phương trình hoành độ giao điểm của hai đồ thị hàm số là:
Số giao điểm của đồ thị (P) và đường thẳng (d) cũng chính là số nghiệm của phương trình (*)
Đồ thị hàm số và chỉ có một điểm chung phương trình có nghiệm kép
Với ta có:
a) Vẽ parabol (P) :y =\(2x^2\)
b) Viết phương trình đường thẳng (d) cắt parabol (P) tại hai điểm A và B có hoành độ lần lượt là -1 và 2
a) Ta có bảng giá trị tương ứng x và y sau :
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = 2x2 | 18 | 8 | 2 | 0 | 2 | 8 | 18 |

Quả parabol hơi xấu tí thông cảm =))
Số giao điểm của parabol y= 2x^2 +3x-1 với đường thẳng y=x-2 là:
PT hoành độ giao điểm:
\(2x^2+3x-1=x-2\\ \Leftrightarrow2x^2+2x+1=0\\ \Delta=4-8< 0\)
Do đó PT vô nghiệm
Vậy parabol không có giao điểm với đt y=x-2
câu 1: a) vẽ parabol (p): y= 1/2x^2 và đường thẳng (d): y=3/2x-1 trên cùng 1 mặt phẳng toạ độ
b) xác định toạ độ giao điểm của (p) và (d) bằng phép toán
câu 2: a) vẽ đồ thị hàm số (p): y=x^2 và (d): Y=-x+2 trên cùng 1 hệ trục toạ độ
b) xác định toạ độ giao điểm của (p) và (d)
câu 3: cho hai hàm số y=x^2 và y=-2x+3
a) vẽ các đồ thị của hai hàm số này trên cùng một hệ trục toạ độ
b) tìm toạ độ giao điểm của hai đồ thị đó
Điều chỉnh a, b, c để vẽ được nhiều dạng parabol khác nhau:
a) \(\)\(y = {x^2} - 3x + 2\)
b) \(y = {x^2}\)
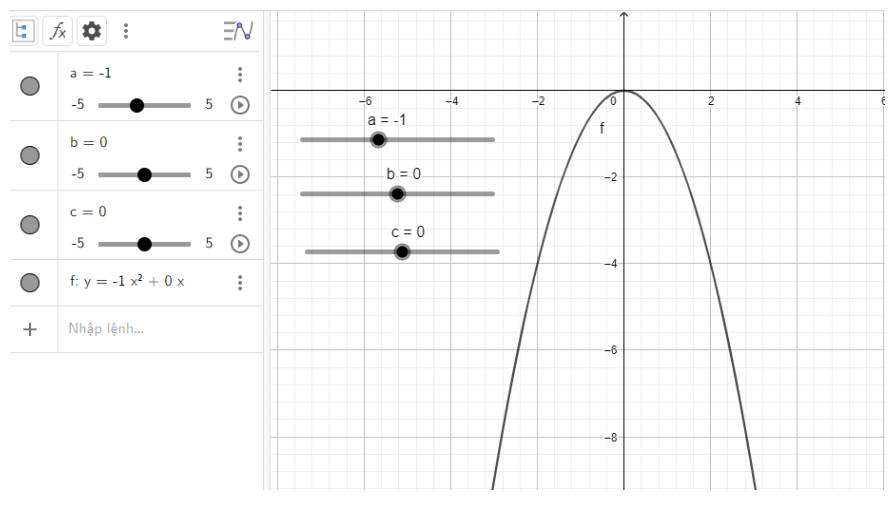
c) \(y = - {x^2}\)
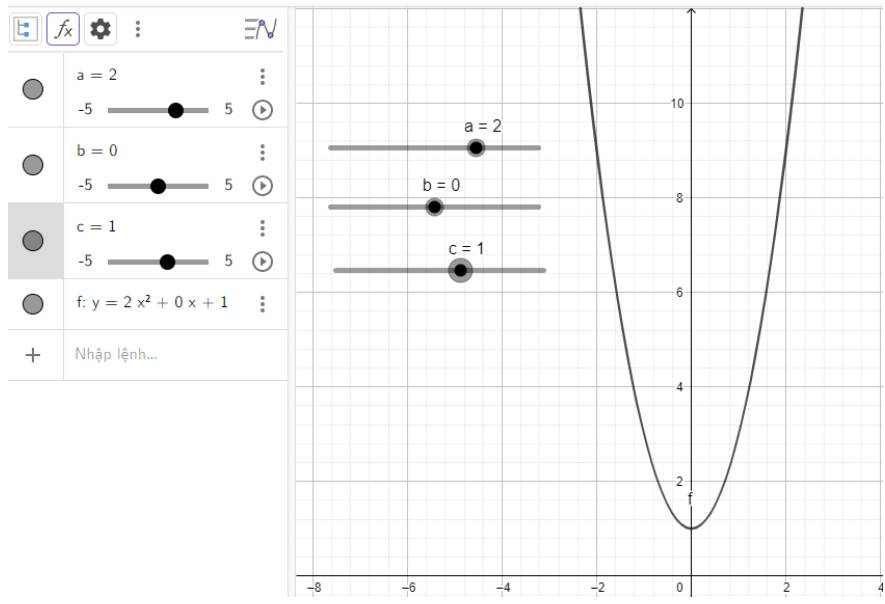
d) \(y = 2{x^2} + 1\)
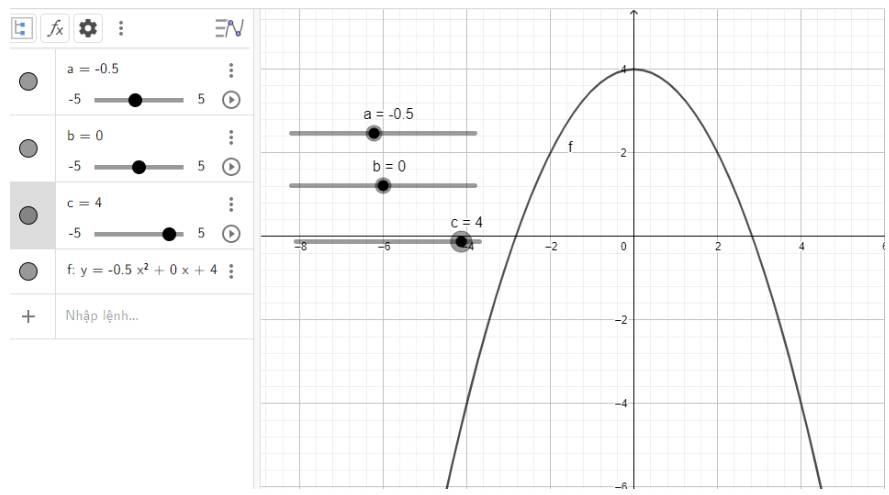
e) \(y = - \frac{1}{2}{x^2} + 4\)
Thực hiện các bước đã nêu ở phương pháp ta có các hình dưới đây
a) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía trên, cắt trục tung và trục hoành lần lượt tại điểm có tọa độ là (0; 2) và (2; 0)
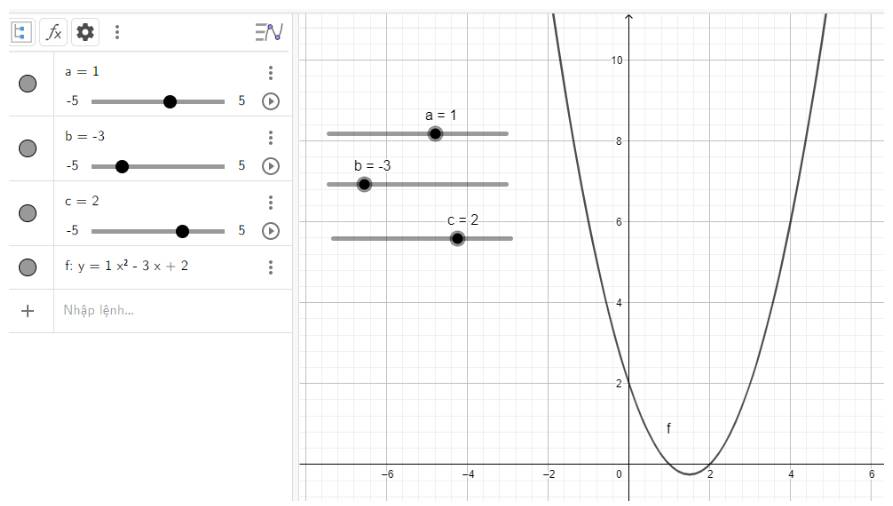
b) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía trên, đi qua gốc tọa độ và đỉnh chính là gốc tọa độ
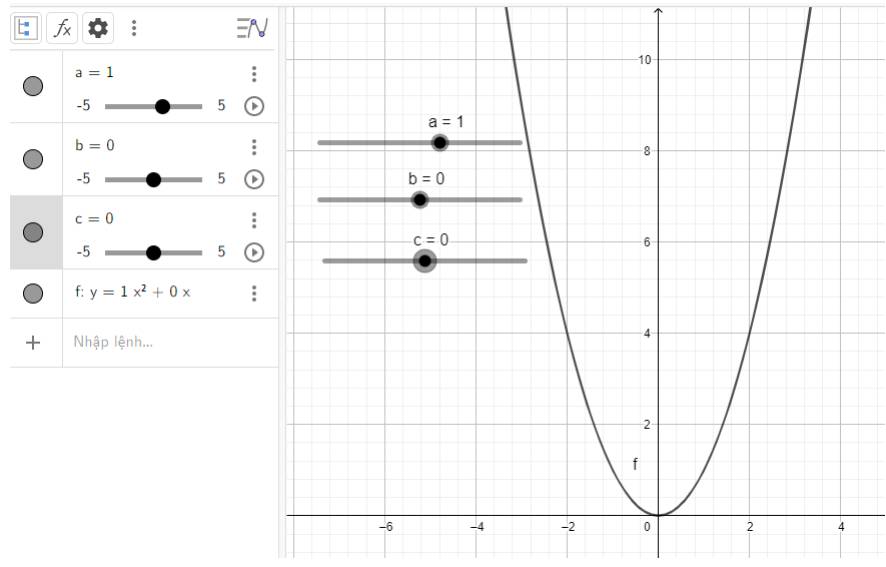
c) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía dưới, đi qua gốc tọa độ và đỉnh chính là gốc tọa độ
d) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía trên, cắt trục tung tại điểm có tung độ là 1 đó cũng chính là đỉnh của parabol
e) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía dưới, cắt trục tung tại điểm có tung độ là 4 đó cũng chính là đỉnh của parabol
VD8: Vẽ đường thẳng (P) của hàm số y=x^2/2. Tìm a,b để đường thẳng y=ax+b đi qua điểm (0;-1) và tiếp xúc với (P)
VD7:a) tìm tọa độ giao điểm của parabol y=1/3x^2 và đg thẳng y=1/6(x+21)
b) với giá trị nào không để đg thẳng y=k(x-1) tiếp xúc với parabol y= 1/3x^2 ?